江苏省徐州市2022-2023学年九年级上学期期末数学试题
试卷更新日期:2023-03-01 类型:期末考试
一、单选题
-
1. 下列图形中,是轴对称图形,但不是中心对称图形的是( )A、
 B、
B、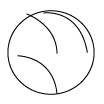 C、
C、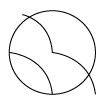 D、
D、 2. 如图,在中, , , , 则的正弦值为( )
2. 如图,在中, , , , 则的正弦值为( ) A、 B、 C、 D、3. 抛物线 的顶点坐标是( )A、(﹣1,2) B、(﹣1,﹣2) C、(1,﹣2) D、(1,2)4. 已知⊙O的半径是4,OP=3,则点P与⊙O的位置关系是( )A、点P在圆上 B、点P在圆内 C、点P在圆外 D、不能确定5. 10件产品中有5件次品,从中任意抽取1件,恰好抽到次品的概率是( )A、 B、 C、 D、6. 将抛物线向右平移1个单位长度,再向上平移2个单位长度,所得到的抛物线为( )A、 B、 C、 D、7. 点B把线段AC分成两部分,如果 =k,那么k的值为( )A、 B、 C、 +1 D、 -18. 有一组数据如下:3,a,4,6,7,它们的平均数是5,那么这组数据的方差是( )A、10 B、 C、2 D、
A、 B、 C、 D、3. 抛物线 的顶点坐标是( )A、(﹣1,2) B、(﹣1,﹣2) C、(1,﹣2) D、(1,2)4. 已知⊙O的半径是4,OP=3,则点P与⊙O的位置关系是( )A、点P在圆上 B、点P在圆内 C、点P在圆外 D、不能确定5. 10件产品中有5件次品,从中任意抽取1件,恰好抽到次品的概率是( )A、 B、 C、 D、6. 将抛物线向右平移1个单位长度,再向上平移2个单位长度,所得到的抛物线为( )A、 B、 C、 D、7. 点B把线段AC分成两部分,如果 =k,那么k的值为( )A、 B、 C、 +1 D、 -18. 有一组数据如下:3,a,4,6,7,它们的平均数是5,那么这组数据的方差是( )A、10 B、 C、2 D、二、填空题
-
9. 已知一组数据的极差为.10. 若 , 且 , 则a的值为.11. 粉笔盒中有10支白色粉笔盒若干支彩色粉笔,每支粉笔除颜色外均相同,从中随机拿一支粉笔,拿到白色的概率为 , 则其中彩色粉笔的数量为支.12. 若圆锥的底面直径为4cm,母线长为5cm,则其侧面积为cm2(结果保留π).13. 如图,OE⊥AB于E,若⊙O的半径为10,OE=6,则AB=.
 14. 甲、乙、丙三人进行飞镖比赛,已知他们每人五次投得的成绩如图6-Z-2所示,那么三人中成绩最稳定的是.
14. 甲、乙、丙三人进行飞镖比赛,已知他们每人五次投得的成绩如图6-Z-2所示,那么三人中成绩最稳定的是. 15. 如图,在中,已知是BC边上的高, , , 则的值为.
15. 如图,在中,已知是BC边上的高, , , 则的值为.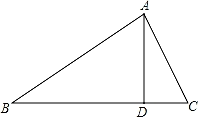 16. 如图,将边长为的正方形绕其中心旋转 , 则两个正方形公共部分(阴影部分)的面积为.
16. 如图,将边长为的正方形绕其中心旋转 , 则两个正方形公共部分(阴影部分)的面积为.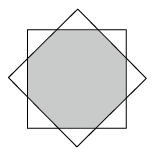
三、解答题
-
17.(1)、计算: ;(2)、解方程:.18. 某人的钱包内有10元、20元和50元的纸币各1张,从中随机取出2张纸币.(1)、求取出纸币的总额是30元的概率;(2)、求取出纸币的总额可购买一件51元的商品的概率.19. 省射击队为从甲、乙两名运动员中选拔一人参加全国比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
第一次
第二次
第三次
第四次
第五次
第六次
甲
10
8
9
8
10
9
乙
10
7
10
10
9
8
(1)、根据表格中的数据,计算出甲的平均成绩是 环,乙的平均成绩是 环;(2)、分别计算甲、乙六次测试成绩的方差;你认为推荐谁参加全国比赛更合适,请说明理由.20. 如图,在平面直角坐标系中,的顶点坐标分别为 , , .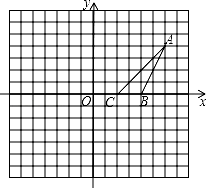 (1)、在y轴左侧,以O为位似中心,画出 , 使它与的相似比为;(2)、根据(1)的作图,.21. 如图,某农场计划建造一个矩形养殖场,为充分利用现有资源,该矩形养殖场一面靠墙(墙的长度为),另外三面用栅栏围成,已知栅栏总长度为 , 设矩形垂直于墙的一边,即的长为.若矩形养殖场的面积为 , 求此时的x的值.
(1)、在y轴左侧,以O为位似中心,画出 , 使它与的相似比为;(2)、根据(1)的作图,.21. 如图,某农场计划建造一个矩形养殖场,为充分利用现有资源,该矩形养殖场一面靠墙(墙的长度为),另外三面用栅栏围成,已知栅栏总长度为 , 设矩形垂直于墙的一边,即的长为.若矩形养殖场的面积为 , 求此时的x的值.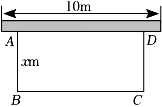 22. 某农户经销一种农产品,已知该产品的进价为每千克20元,调查发现,该产品每天的销量y(千克)与售价x(元/千克)有如下关系: , 设该产品每天的销售利润为w元.(1)、售价为多少时,每天的销售利润最大?最大利润是多少?(2)、物价部门规定该产品的售价不得高于28元/千克,该农户若每天获利150元,售价应定为多少?23. 小红和爸爸绕着小区广场锻炼如图在矩形广场 边 的中点 处有一座雕塑.在某一时刻,小红到达点 处,爸爸到达点 处,此时雕塑在小红的南偏东 方向,爸爸在小红的北偏东 方向,若小红到雕塑的距离 ,求小红与爸爸的距离 .(结果精确到 ,参考数据: , , )
22. 某农户经销一种农产品,已知该产品的进价为每千克20元,调查发现,该产品每天的销量y(千克)与售价x(元/千克)有如下关系: , 设该产品每天的销售利润为w元.(1)、售价为多少时,每天的销售利润最大?最大利润是多少?(2)、物价部门规定该产品的售价不得高于28元/千克,该农户若每天获利150元,售价应定为多少?23. 小红和爸爸绕着小区广场锻炼如图在矩形广场 边 的中点 处有一座雕塑.在某一时刻,小红到达点 处,爸爸到达点 处,此时雕塑在小红的南偏东 方向,爸爸在小红的北偏东 方向,若小红到雕塑的距离 ,求小红与爸爸的距离 .(结果精确到 ,参考数据: , , )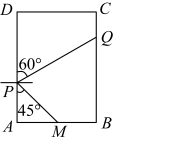 24. 如图,AB是⊙O的直径,过点B作⊙O的切线BM,弦CD//BM,交AB于点F,且 , 连接AC,AD,延长AD交BM于点E.
24. 如图,AB是⊙O的直径,过点B作⊙O的切线BM,弦CD//BM,交AB于点F,且 , 连接AC,AD,延长AD交BM于点E.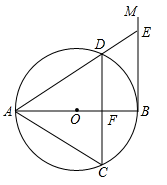 (1)、求证:△ACD是等边三角形;(2)、连接OE,若DE=2,求OE的长.25. 我们知道:如图①,点B把线段AC分成两部分,如果= , 那么称点B为线段AC的黄金分割点.它们的比值为.
(1)、求证:△ACD是等边三角形;(2)、连接OE,若DE=2,求OE的长.25. 我们知道:如图①,点B把线段AC分成两部分,如果= , 那么称点B为线段AC的黄金分割点.它们的比值为.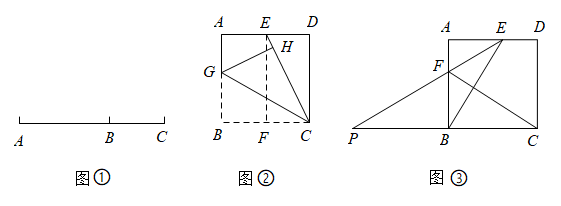 (1)、在图①中,若AC=20cm,则AB的长为cm;(2)、如图②,用边长为20cm的正方形纸片进行如下操作:对折正方形ABCD得折痕EF,连接CE,将CB折叠到CE上,点B对应点H,得折痕CG.试说明:G是AB的黄金分割点;(3)、如图③,小明进一步探究:在边长为a的正方形ABCD的边AD上任取点E(AE>DE),连接BE,作CF⊥BE,交AB于点F,延长EF、CB交于点P.他发现当PB与BC满足某种关系时,E、F恰好分别是AD、AB的黄金分割点.请猜想小明的发现,并说明理由.
(1)、在图①中,若AC=20cm,则AB的长为cm;(2)、如图②,用边长为20cm的正方形纸片进行如下操作:对折正方形ABCD得折痕EF,连接CE,将CB折叠到CE上,点B对应点H,得折痕CG.试说明:G是AB的黄金分割点;(3)、如图③,小明进一步探究:在边长为a的正方形ABCD的边AD上任取点E(AE>DE),连接BE,作CF⊥BE,交AB于点F,延长EF、CB交于点P.他发现当PB与BC满足某种关系时,E、F恰好分别是AD、AB的黄金分割点.请猜想小明的发现,并说明理由.