江苏省宿迁市宿城区2022-2023学年九年级上学期期末数学试题
试卷更新日期:2023-03-01 类型:期末考试
一、单选题
-
1. 方程的解为( )A、 B、 C、 D、2. 一组数据0、、2、、1的极差是( )A、2 B、3 C、4 D、53. 抛物线与y轴的交点坐标是( )A、(0,2) B、( , 0) C、(2,0) D、(0,)4. 已知 , 则的值为( )A、 B、 C、 D、5. 如图,AB是⊙O直径,若∠AOC=140°,则∠D的度数是( )
 A、20° B、30° C、40° D、70°6. 对于函数 ,下列结论错误的是( )A、图象顶点是(2,5) B、图象开口向上 C、图象关于直线 对称 D、函数最大值为57. 如图,利用标杆BE测量建筑物的高度,已知标杆高 , 测得.则建筑物的高是( )
A、20° B、30° C、40° D、70°6. 对于函数 ,下列结论错误的是( )A、图象顶点是(2,5) B、图象开口向上 C、图象关于直线 对称 D、函数最大值为57. 如图,利用标杆BE测量建筑物的高度,已知标杆高 , 测得.则建筑物的高是( ) A、 B、 C、 D、8. 从甲,乙,丙三人中任选两名代表,甲被选中的可能性是( )A、 B、 C、 D、9. 若二次函数的图象经过点 , 则方程的解为( )A、 B、 C、 D、10. 如图,抛物线与x轴交于A、B两点,抛物线的顶点为D,点C为的中点,以C为圆心,长为半径在x轴的上方作一个半圆,点E为半圆上一动点,连接 , 取的中点F,当点E沿着半圆从点A运动至点B的过程中,线段 的最小值为( )
A、 B、 C、 D、8. 从甲,乙,丙三人中任选两名代表,甲被选中的可能性是( )A、 B、 C、 D、9. 若二次函数的图象经过点 , 则方程的解为( )A、 B、 C、 D、10. 如图,抛物线与x轴交于A、B两点,抛物线的顶点为D,点C为的中点,以C为圆心,长为半径在x轴的上方作一个半圆,点E为半圆上一动点,连接 , 取的中点F,当点E沿着半圆从点A运动至点B的过程中,线段 的最小值为( )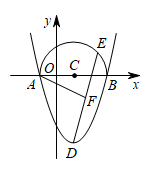 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
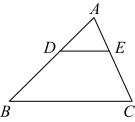
11. 在一次跳远训练中,甲、乙两人每人5次跳远的平均成绩都是米,方差分别是(米),(米),则在这次跳远训练中成绩比较稳定的是.12. 关于 的一元二次方程 有两个实数根,则 的取值范围是.13. 如图,中,点D、E分别在线段、上, , 若 , , , 则的长是 .
 14. 点C是线段AB的黄金分割点,.若 , 则cm.15. 已知抛物线经过点两点,则、的大小关系是 .16. 将抛物线 先向右平移1个单位,再向下平移3个单位后得到新的抛物线,则新抛物线对应的函数表达式是.17. 如图,四边形是菱形,点C在以O为圆心为半径的上,若 , 则的长为.
14. 点C是线段AB的黄金分割点,.若 , 则cm.15. 已知抛物线经过点两点,则、的大小关系是 .16. 将抛物线 先向右平移1个单位,再向下平移3个单位后得到新的抛物线,则新抛物线对应的函数表达式是.17. 如图,四边形是菱形,点C在以O为圆心为半径的上,若 , 则的长为.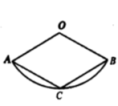 18. 在平面直角坐标系中,已知点 , 点 , 点 , 动点D从A点出发,以每秒1个单位的速度水平向右运动,动点E从点B出发,以每秒1个单位的速度竖直向上运动,过点A作交于点G,当线段的值最小时,则运动时间t的值为 .
18. 在平面直角坐标系中,已知点 , 点 , 点 , 动点D从A点出发,以每秒1个单位的速度水平向右运动,动点E从点B出发,以每秒1个单位的速度竖直向上运动,过点A作交于点G,当线段的值最小时,则运动时间t的值为 .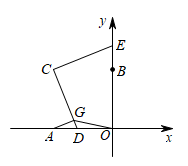
三、解答题
-
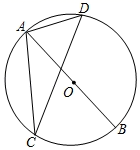
19. 解下列方程:(1)、.(2)、.20. 已知x=﹣1是方程x2+mx﹣5=0的一个根,求m的值及方程的另一个根.21. 如图, 是 直径, 是 的弦, ,求 的度数.
 22. 某中学运动队有短跑、长跑、跳远、实心球四个训练小队,现将四个训练小队队员情况绘制成如下不完整的统计图:
22. 某中学运动队有短跑、长跑、跳远、实心球四个训练小队,现将四个训练小队队员情况绘制成如下不完整的统计图: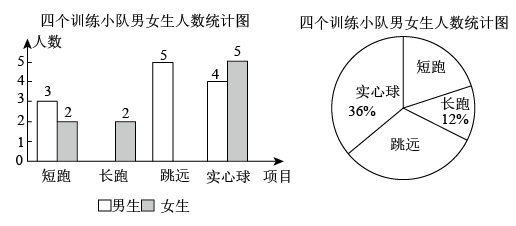 (1)、学校运动队的队员总人数为;(2)、补全条形统计图,并标明数据;(3)、若在长跑训练小组中随机选取2名同学进行比赛,请用列举法(画树状图或列表)求所选取的这两名同学恰好是一男一女的概率.23. 如图,在正方形网格中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格图中进行下列操作:
(1)、学校运动队的队员总人数为;(2)、补全条形统计图,并标明数据;(3)、若在长跑训练小组中随机选取2名同学进行比赛,请用列举法(画树状图或列表)求所选取的这两名同学恰好是一男一女的概率.23. 如图,在正方形网格中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格图中进行下列操作: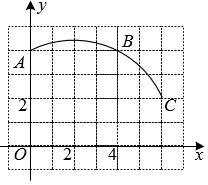 (1)、利用网格确定该圆弧所在圆的圆心D点的位置,则D点坐标为;(2)、连接AD、CD,则⊙D的半径为(结果保留根号),∠ADC的度数为;(3)、若扇形DAC是一个圆锥的侧面展开图,求该圆锥底面半径.(结果保留根号).24. 如图,在中, , 点D、E分别在、上,且.
(1)、利用网格确定该圆弧所在圆的圆心D点的位置,则D点坐标为;(2)、连接AD、CD,则⊙D的半径为(结果保留根号),∠ADC的度数为;(3)、若扇形DAC是一个圆锥的侧面展开图,求该圆锥底面半径.(结果保留根号).24. 如图,在中, , 点D、E分别在、上,且.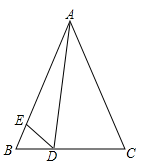 (1)、与相似吗?为什么?(2)、求证:.25. 掷实心球是中考体育考试项目之一.如图1是一名男生投实心球情境,实心球行进路线是条抛物线,行进高度与水平距离之间的函数关系如图2所示.掷出时,起点处高度为.当水平距离为时,实心球行进至最高点处.
(1)、与相似吗?为什么?(2)、求证:.25. 掷实心球是中考体育考试项目之一.如图1是一名男生投实心球情境,实心球行进路线是条抛物线,行进高度与水平距离之间的函数关系如图2所示.掷出时,起点处高度为.当水平距离为时,实心球行进至最高点处.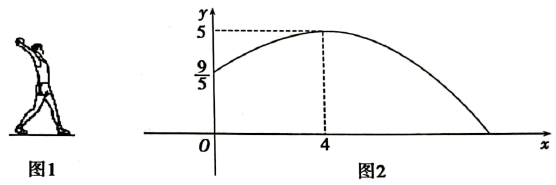 (1)、求y关于x的函数表达式;(2)、根据中考体育考试评分标准(男生版),投据过程中,实心球从起点到落地点的水平距离大于等于时,即可得满分分.该男生在此项考试中能否得满分,请说明理由.26. 已知,如图,为的直径,内接于 , 点P是的内心,延长交于点D,连接.
(1)、求y关于x的函数表达式;(2)、根据中考体育考试评分标准(男生版),投据过程中,实心球从起点到落地点的水平距离大于等于时,即可得满分分.该男生在此项考试中能否得满分,请说明理由.26. 已知,如图,为的直径,内接于 , 点P是的内心,延长交于点D,连接. (1)、求证:;(2)、已知的半径是 , , 求的长.27. 概念生成:定义:我们把经过三角形的一个顶点并与其对边所在直线相切的圆叫做三角形的“切接圆”,如图1, , 经过点A,并与点A的对边相切于点D,则该就叫做的切接圆.根据上述定义解决下列问题:
(1)、求证:;(2)、已知的半径是 , , 求的长.27. 概念生成:定义:我们把经过三角形的一个顶点并与其对边所在直线相切的圆叫做三角形的“切接圆”,如图1, , 经过点A,并与点A的对边相切于点D,则该就叫做的切接圆.根据上述定义解决下列问题: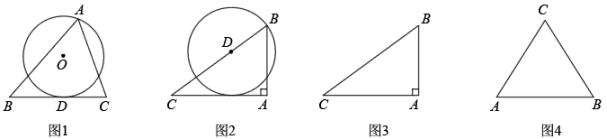 (1)、已知,中, , , .
(1)、已知,中, , , .①如图2,若点D在边上, , 以D为圆心,长为半径作圆,则是的“切接圆”吗?请说明理由.
②在图3中,若点D在的边上,以D为圆心,长为半径作圆,当是的“切接圆”时,求的半径(直接写出答案).
思维拓展
(2)、如图4,中,. , 把放在平面直角坐标系中,使点C落在y轴上,边落在x轴上.试说明:以抛物线图像上任意一点为圆心都可以作过点C的的“切接圆”.28. 已知,如图,抛物线与x轴交于A、B两点,与y轴交于点C, , 点P为x轴下方的抛物线上一点.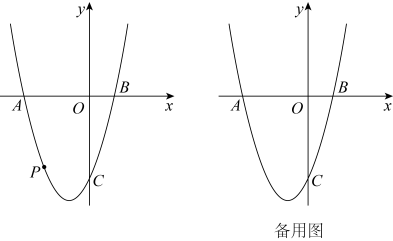 (1)、求抛物线的函数表达式;(2)、连接 , 求四边形面积的最大值;(3)、是否存在这样的点P,使得点P到和两边的距离相等,若存在,请求出点P的坐标;若不存在,请说明理由.
(1)、求抛物线的函数表达式;(2)、连接 , 求四边形面积的最大值;(3)、是否存在这样的点P,使得点P到和两边的距离相等,若存在,请求出点P的坐标;若不存在,请说明理由.