江苏省宿迁市沭阳县2022-2023学年九年级上学期期末数学试题
试卷更新日期:2023-03-01 类型:期末考试
一、单选题
-
1. 在下列二次函数中,图象的开口向下,顶点坐标为(-2,-1)的是( )A、 B、 C、 D、2. 已知、、、、是按从小到大顺序排列的5个连续整数,若将这组数据变为、、、、 , 则这组新数据与原来相比( )A、平均数变大 B、中位数变小 C、极差变大 D、方差变小3. 已知 , 则下列错误的是( )A、 B、 C、 D、4. 下列图形中,不是相似图形的一组是( )A、
 B、
B、 C、
C、 D、
D、 5. 如图,中,点D是边上一点,下列条件中,不能判定与相似的是( )
5. 如图,中,点D是边上一点,下列条件中,不能判定与相似的是( )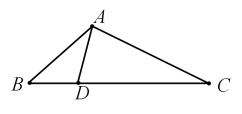 A、 B、 C、 D、6. 在直角三角形ABC中, , 则的值是( )A、 B、 C、 D、37. 如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-5,0),对称轴为直线x=-2,给出四个结论:①abc>0;②4a-b=0;③若点B(-3,y1).C(0,y2)为函数图象上的两点,则y1<y2;④a+b+c=0;其中,正确结论的个数是( )
A、 B、 C、 D、6. 在直角三角形ABC中, , 则的值是( )A、 B、 C、 D、37. 如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-5,0),对称轴为直线x=-2,给出四个结论:①abc>0;②4a-b=0;③若点B(-3,y1).C(0,y2)为函数图象上的两点,则y1<y2;④a+b+c=0;其中,正确结论的个数是( )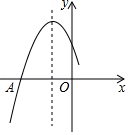 A、1 B、2 C、3 D、48. 如图,在中, , , , 以O为圆心,4为半径作圆O,交两边于点C,D,P为劣弧CD上一动点,则最小值为( ).
A、1 B、2 C、3 D、48. 如图,在中, , , , 以O为圆心,4为半径作圆O,交两边于点C,D,P为劣弧CD上一动点,则最小值为( ).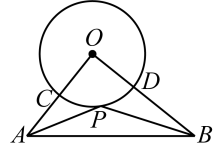 A、13 B、 C、 D、
A、13 B、 C、 D、二、填空题
-
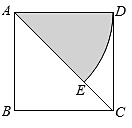
9. 已知是一元二次方程的一个解,则m的值为.10. 为了测量旗杆的高度,某同学测得阳光下旗杆的影长为2m,同一时刻长度为1m的标杆影长为0.4m,则旗杆的高度为m.11. 平面直角坐标系内有点 , 若与x轴的锐角夹角为 , 则的值为.12. 在△ABC中,如果 , 则∠C=.13. 在一个不透明的袋子里装有红球、黄球共20个,这些球除颜色外都相同,小红通过多次试验发现,摸出红球的频率稳定在0.4左右,则袋子里黄球的个数最有可能是.14. 如图,正方形 的边长为4,以点 为圆心, 为半径,画圆弧 得到扇形 (阴影部分,点 在对角线 上).若扇形 正好是一个圆锥的侧面展开图,则该圆锥的底面圆的半径是.
 15. 如图,点A,B,C在上, , 则等于 °.
15. 如图,点A,B,C在上, , 则等于 °.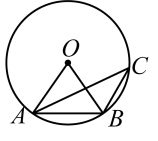 16. 如图,D、E分别是ΔABC的边AB、AC上的动点,若 , 且ΔADE与ΔABC相似,则AD的长度是.
16. 如图,D、E分别是ΔABC的边AB、AC上的动点,若 , 且ΔADE与ΔABC相似,则AD的长度是.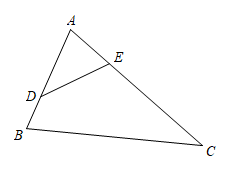 17. 已知函数在的最大值是1,最小值是 , 则m的取值范围是.18. 将一副三角尺(在Rt△ABC中,∠ACB=90°,∠B=60°;在Rt△EDF中,∠EDF=90°,∠E=45°)如图摆放,点D为AB的中点,DE交AC于点P,DF经过点C.将△EDF绕点D顺时针方向旋转角 , 交AC于点M,交BC于点N,则的值为.
17. 已知函数在的最大值是1,最小值是 , 则m的取值范围是.18. 将一副三角尺(在Rt△ABC中,∠ACB=90°,∠B=60°;在Rt△EDF中,∠EDF=90°,∠E=45°)如图摆放,点D为AB的中点,DE交AC于点P,DF经过点C.将△EDF绕点D顺时针方向旋转角 , 交AC于点M,交BC于点N,则的值为.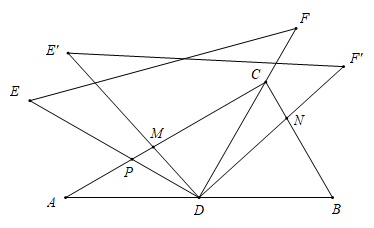
三、解答题
-
19.(1)、解方程:;(2)、计算.20. 如图,在平面直角坐标系中,过格点A、B、C作一圆弧.
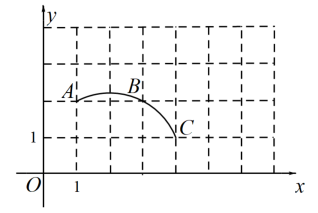 (1)、直接写出该圆弧所在圆的圆心D的坐标.(2)、求弧AC的长(结果保留).(3)、连接AC、BC,则.21. 如图,△ABC中,D是BC上一点,∠DAC=∠B,E为AB上一点.
(1)、直接写出该圆弧所在圆的圆心D的坐标.(2)、求弧AC的长(结果保留).(3)、连接AC、BC,则.21. 如图,△ABC中,D是BC上一点,∠DAC=∠B,E为AB上一点. (1)、求证:△CAD∽△CBA;(2)、若BD=10,DC=8,求AC的长;(3)、在(2)的条件下,若DE∥AC,AE=4,求BE的长.22. 为了从甲、乙两位同学中选拔一人参加知识竞赛,举行了6次选拔赛,根据两位同学6次选拔赛的成绩,分别绘制了如图统计图.
(1)、求证:△CAD∽△CBA;(2)、若BD=10,DC=8,求AC的长;(3)、在(2)的条件下,若DE∥AC,AE=4,求BE的长.22. 为了从甲、乙两位同学中选拔一人参加知识竞赛,举行了6次选拔赛,根据两位同学6次选拔赛的成绩,分别绘制了如图统计图.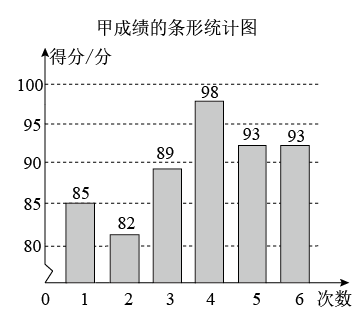
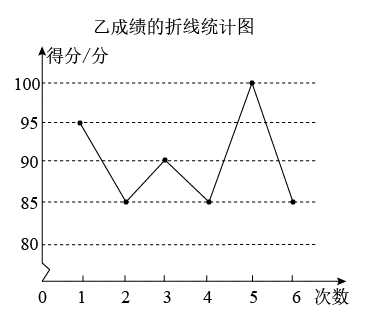 (1)、填写下列表格
(1)、填写下列表格平均数/分
中位数/分
众数/分
甲
90
①
93
乙
②
87.5
③
(2)、已求得甲同学6次成绩的方差为(分2),求出乙同学6次成绩的方差;(3)、你认为选择哪一位同学参加知识竞赛比较好?请说明理由.23. 小明的爸妈购买车票,高铁售票系统随机分配座位,若系统已将两人分配到同一排. (1)、小明的爸爸购得A座票后,妈妈购得B座票的概率是;(2)、求分给二人相邻座位(过道两侧座位C、D不算相邻)的概率.24. 根据对某市相关的市场物价调研,预计进入夏季后的某一段时间,某批发市场内的甲种蔬菜的销售利润 (千元)与进货量 (吨)之间的函数 的图象如图①所示,乙种蔬菜的销售利润 (千元)与进货量 (吨)之间的函数 的图象如图②所示.
(1)、小明的爸爸购得A座票后,妈妈购得B座票的概率是;(2)、求分给二人相邻座位(过道两侧座位C、D不算相邻)的概率.24. 根据对某市相关的市场物价调研,预计进入夏季后的某一段时间,某批发市场内的甲种蔬菜的销售利润 (千元)与进货量 (吨)之间的函数 的图象如图①所示,乙种蔬菜的销售利润 (千元)与进货量 (吨)之间的函数 的图象如图②所示.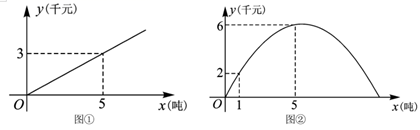 (1)、分别求出 、 与 之间的函数关系式;(2)、如果该市场准备进甲、乙两种蔬菜共 吨,设乙种蔬菜的进货量为 吨.
(1)、分别求出 、 与 之间的函数关系式;(2)、如果该市场准备进甲、乙两种蔬菜共 吨,设乙种蔬菜的进货量为 吨.①写出这两种蔬菜所获得的销售利润之和 (千元)与 (吨)之间的函数关系式.并求当这两种蔬菜各进多少吨时获得的销售利润之和最大,最大利润是多少元?
②为了获得两种蔬菜的利润之和不少于 元,则乙种蔬菜进货量应在什么范围内合适?
25. 如图,为⊙外一点, , 为⊙上两点, , 垂足为 , 交⊙于点 , 交于 , .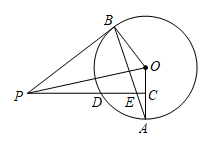 (1)、求证:为⊙的切线;(2)、若 , , 求的长.26. 杭州市西湖风景区的雷峰塔又名“皇妃塔”,某校社会实践小组为了测量雷峰塔的高度,在地面上C处垂直于地面竖立了高度为2米的标杆 , 这时地面上的点E,标杆的顶端点D,雷峰塔的塔尖点B正好在同一直线上,测得米,将标杆向后平移到点G处,这时地面上的点F,标杆的顶端点H,雷峰塔的塔尖点B正好又在同一直线上(点F,点G,点E,点C与塔底处的点A在同一直线上),这时测得米,米,请你根据以上数据,计算雷峰塔的高度.
(1)、求证:为⊙的切线;(2)、若 , , 求的长.26. 杭州市西湖风景区的雷峰塔又名“皇妃塔”,某校社会实践小组为了测量雷峰塔的高度,在地面上C处垂直于地面竖立了高度为2米的标杆 , 这时地面上的点E,标杆的顶端点D,雷峰塔的塔尖点B正好在同一直线上,测得米,将标杆向后平移到点G处,这时地面上的点F,标杆的顶端点H,雷峰塔的塔尖点B正好又在同一直线上(点F,点G,点E,点C与塔底处的点A在同一直线上),这时测得米,米,请你根据以上数据,计算雷峰塔的高度.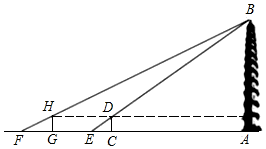 27. 感知:数学课上,老师给出了一个模型:如图1,点在直线上,且 , 像这种一条直线上的三个顶点含有三个相等的角的模型我们把它称为“一线三等角”模型.
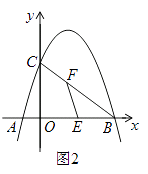
27. 感知:数学课上,老师给出了一个模型:如图1,点在直线上,且 , 像这种一条直线上的三个顶点含有三个相等的角的模型我们把它称为“一线三等角”模型.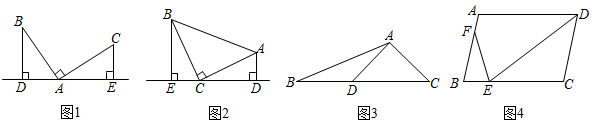 (1)、如图2,中, , , 直线经过点 , 过作于点 , 过作于点 . 求证:;(2)、如图3,在中,是上一点, , , , , 求点到边的距离;(3)、如图4,在中,为边上的一点,为边上的一点.若 , , , 求的值.28. 如图1,在平面直角坐标系中,直线l与x轴、y轴分别交于点B(4,0)、C(0,3),点A为x轴负半轴上一点,AM⊥BC于点M交y轴于点N(0, ).已知抛物线y=ax2+bx+c经过点A,B,C.
(1)、如图2,中, , , 直线经过点 , 过作于点 , 过作于点 . 求证:;(2)、如图3,在中,是上一点, , , , , 求点到边的距离;(3)、如图4,在中,为边上的一点,为边上的一点.若 , , , 求的值.28. 如图1,在平面直角坐标系中,直线l与x轴、y轴分别交于点B(4,0)、C(0,3),点A为x轴负半轴上一点,AM⊥BC于点M交y轴于点N(0, ).已知抛物线y=ax2+bx+c经过点A,B,C.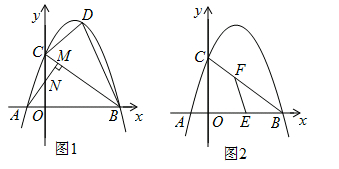 (1)、求抛物线的函数式.(2)、连接AC,点D在线段BC上方的抛物线上,连接DC,DB,若△BCD和△ABC面积满足S△BCD= S△ABC , 求点D的坐标.
(1)、求抛物线的函数式.(2)、连接AC,点D在线段BC上方的抛物线上,连接DC,DB,若△BCD和△ABC面积满足S△BCD= S△ABC , 求点D的坐标.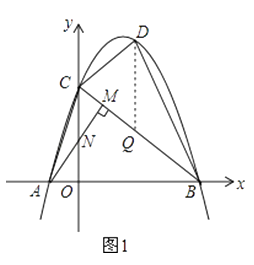 (3)、如图2,E为OB中点,设F为线段BC上一点(不含端点),连接EF.一动点P从E出发,沿线段EF以每秒3个单位的速度运动到F,再沿着线段PC以每秒5个单位的速度运动到C后停止.若点P在整个运动过程中用时最少,请直接写出最少时间和此时点F的坐标.
(3)、如图2,E为OB中点,设F为线段BC上一点(不含端点),连接EF.一动点P从E出发,沿线段EF以每秒3个单位的速度运动到F,再沿着线段PC以每秒5个单位的速度运动到C后停止.若点P在整个运动过程中用时最少,请直接写出最少时间和此时点F的坐标.