江苏省泰州市兴化市2022-2023学年九年级上学期期末数学试题

试卷更新日期：2023-03-01 类型：期末考试

进入出卷网下载

一、单选题

1. 据了解，某定点医院收治的6名“新型冠状肺炎”患者的新冠病毒潜伏期分别为2天，3天，3天，3天，4天，5天，则这6名患者新冠病毒潜伏期的众数为（　　）

A、2天 B、3天 C、4天 D、5天

查看试题解析
2. 已知线段 $a = 9$ ， $b = 1$ ，如果线段c是线段a、b的比例中项，那么c=（　　）

A、±3 B、3 C、4.5 D、5

查看试题解析
3. 二次函数y=x²图象向右平移3个单位，得到新图象的函数表达式是（　　）

A、y=x²+3 B、y=x²-3 C、y=（x+3）² D、y=（x-3）²

查看试题解析
4. 如图，在⊙O中，∠BOC＝130°，点A在 $\overset{⌢}{B A C}$ 上，则∠BAC的度数为（）

A、55° B、65° C、75° D、130°

查看试题解析
5. 在 $△ A B C$ 中， $∠ C = 90 °$ ， $t a n A = 2$ ，则 $s i n A$ 的值为（　　）

A、 $\frac{2 \sqrt{5}}{5}$ B、 $\frac{\sqrt{5}}{5}$ C、 $\frac{1}{2}$ D、2

查看试题解析
6. 已知圆锥的底面半径为2，母线长为6，则它的侧面展开图的面积是（　　）

A、12 B、24 C、12π D、24π

查看试题解析

二、填空题

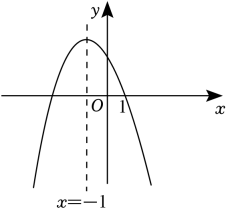
7. 已知⊙O的半径是5，OP=4，则点P与⊙O的位置关系是：点P在⊙O.

查看试题解析
8. 若 $△ A B C ∽ △ D E F$ ，它们的面积比为 $9 ： 4$ ，则它们的对应高的比为 .

查看试题解析
9. 已知二次函数 $y = a x^{2} + b x + c$ 的图象如图所示，则一元二次方程 $a x^{2} + b x + c = 0$ 的解是 .

查看试题解析
10. 某校体育期末考核“仰卧起坐”和“ $800$ 米”两项，并按 $3 ： 7$ 的比例算出期末成绩.已知小林这两项的考试成绩分别为 $80$ 分、 $90$ 分，则小林的体育期末成绩为分.

查看试题解析
11. 如图，平面直角坐标系中，正方形 $E F B G$ 和正方形 $A B C D$ 是以O为位似中心的位似图形，位似比为1：2，点F，B，C在x轴上，若 $A D = 6$ ，则点G的坐标为 .

查看试题解析
12. 如果一组数据3，5，x，6，8的众数为3，那么这组数据的方差为 .

查看试题解析
13. 已知线段 $A B = 4 c m$ ， C是AB的黄金分割点，且 $A C > B C$ ，则 $A C =$ .（结果保留根号）

查看试题解析
14. 如图，在 $R t △ A B C$ 中， $∠ A B C = 90 °$ ， $B D ⊥ A C$ 于点 $D ， A C = 10$ ， $c o s C = \frac{3}{5}$ ，那么 $C D =$ ．

查看试题解析
15. 如图，抛物线 $y = a x^{2} + c$ 与直线 $y = m x + n$ 交于两点 $A (- 1 ， p)$ ， $B (4 ， q)$ ，则不等式 $a x^{2} - m x + c < n$ 的解集是.

查看试题解析
16. 如图，半径为7的扇形 $O A B$ 中， $∠ O = 60 °$ ， $C$ 为半径 $O A$ 上一点，过 $C$ 作 $C D ⊥ O B$ 于点D，以 $C D$ 为边向右作等边 $△ C D E$ ，当点E落在 $\overset{⌢}{A B}$ 上时， $C D =$ .

查看试题解析

三、解答题

17. 某校举行“中国共产党十九大”知识问答竞赛.每班选20名同学参加比赛.根据答对的题目数量得分，等级分为5分，4分，3分，2分.学校将八年级甲班和乙班的成绩整理并绘制成如下的统计图.
甲班知识问答成绩统计图乙班知识问答成绩统计图
甲、乙两班成绩统计表
班级
平均数（分）
中位数（分）
众数（分）
甲班
a
4
4
乙班
3.6
3.5
b

(1)、请把甲班知识问答成绩统计图补充完整.

(2)、通过统计得到上表，请求出表中数据a，b的值.

(3)、根据（2）的结果，你认为甲，乙两班哪个班级成绩更好？写出你的理由.

查看试题解析
18. 如图，已知 $∠ B A C = ∠ E A F$ ， $∠ A B E = ∠ A C F$ ，若B，E，F三点共线，线段 $E F$ 与 $A C$ 交于点O.

(1)、求证： $△ A B E ∽ △ A C F$ ；

(2)、若 $A B = 3$ ， $C F = 4$ ， $△ A O B$ 的面积为9，求 $△ C O F$ 的面积.

查看试题解析
19. 如图，某测量队采用无人机技术测量无法直达的A，B两处的直线距离，已知在无人机的镜头O处测得A，B的俯角分别为 $45 °$ 和 $50 °$ ，无人机的飞行高度 $O C$ 为 $238$ 米，点A，B，C在同一直线上，求 $A B$ 的长度（结果保留整数，参考数据： $s i n 50 ° \approx 0.77$ ， $t a n 50 ° \approx 1.19$ ）.

查看试题解析
20. 已知， $A B$ 为 $⊙ O$ 的弦，且 $A O ⊥ B O$ .

(1)、如图1，若 $O A = 2$ ，求阴影部分的面积；

(2)、如图2，若点C为 $A B$ 的中点，点D为 $O B$ 的中点.请仅用无刻度的直尺过点B作 $⊙ O$ 的的切线.

查看试题解析
21. 如图，已知抛物线 $y = - x^{2} + a x$ 经过点 $A (4 ， 0)$ 和点 $B (1 ， m)$ ，其对称轴交x轴于点H，点C是抛物线在直线 $A B$ 上方的一个动点（不含A，B两点）.

(1)、求a、m的值.

(2)、连接 $A B$ 、 $O B$ ，若 $△ A O B$ 的面积是 $△ A B C$ 的面积的2倍，求点C的坐标.

(3)、若直线 $A C$ 、 $O C$ 分别交该抛物线的对称轴于点D、E，试问 $D H + E H$ 是否为定值，若是，请求出该定值；若不是，请说明理由.

查看试题解析
22. 如图，在等腰 $△ A B C$ 中，已知 $A B ＝ A C ＝ 5$ ， $B C = 6$ ， D为 $A B$ 上一点，过点D作 $D E ⊥ A B$ 交 $B C$ 边于点E，过点E作 $E F ⊥ B C$ 交 $A C$ 边于点F.

(1)、求 $c o s B$ 的值；

(2)、当 $B D$ 长为何值时，以点F为圆心，线段 $F A$ 为半径的圆与 $B C$ 边相切；

(3)、过点F作 $F P ⊥ A C$ ，与线段 $D E$ 交于点G，设 $B D$ 长为t， $△ E F G$ 的面积为S，求S关于t的函数表达式及t的取值范围.

查看试题解析

班级	平均数（分）	中位数（分）	众数（分）
甲班	a	4	4
乙班	3.6	3.5	b