江苏省泰州市泰兴市2022-2023学年九年级上学期期末数学试题
试卷更新日期:2023-03-01 类型:期末考试
一、单选题
-
1. 下列方程中,是一元二次方程的是( )A、2x+y=1 B、x2+3xy=6 C、x+ =4 D、x2=3x﹣22. 若2x=5y,则下列式子中错误的是( )A、 B、 C、 D、3. 在Rt△ABC中,∠C=90°,各边都扩大5倍,则tanA的值( )A、不变 B、扩大5倍 C、缩小5倍 D、不能确定4. 已知一组数据a、b、c、d的平均数是3,在这组数据后再添加数据3得到一组新数据a、b、c、d、3,则新数据与原数据相比,方差将( )A、不变 B、变大 C、变小 D、不能确定5. 如图,四边形内接于 , , , 则( )
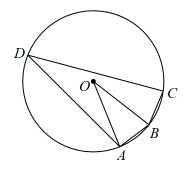 A、 B、 C、 D、无法确定6. 已知二次函数 , 对于其图像和性质,下列说法错误的是( )A、图像开口向下 B、图像经过原点 C、当时,y随x的增大而减小,则 D、当时,y随x的增大而增大
A、 B、 C、 D、无法确定6. 已知二次函数 , 对于其图像和性质,下列说法错误的是( )A、图像开口向下 B、图像经过原点 C、当时,y随x的增大而减小,则 D、当时,y随x的增大而增大二、填空题
-
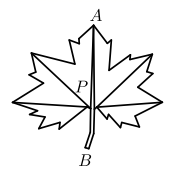
7. 方程的解为.8. 大自然是美的设计师,即使是一片小小的树叶,也蕴含着“黄金分割”.如图, 为 的黄金分割点 ,如果 的长度为 ,那么 的长度是.
 9. 将抛物线向上平移3个单位长度,所得抛物线解析式为.10. 如图,以点O为位似中心,将 放大后得到 , ,则 .
9. 将抛物线向上平移3个单位长度,所得抛物线解析式为.10. 如图,以点O为位似中心,将 放大后得到 , ,则 .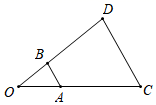 11. 一个圆锥的底面半径和高都是 , 则圆锥的侧面积为.(结果保留)12. 已知锐角中, , , 则的长为.13. 已知a、b是方程的根,则式子的值为.14. 如图是一座圆弧型拱桥的截面示意图,若桥面跨度米,拱高米(C为的中点,D为弧的中点).则桥拱所在圆的半径为米.
11. 一个圆锥的底面半径和高都是 , 则圆锥的侧面积为.(结果保留)12. 已知锐角中, , , 则的长为.13. 已知a、b是方程的根,则式子的值为.14. 如图是一座圆弧型拱桥的截面示意图,若桥面跨度米,拱高米(C为的中点,D为弧的中点).则桥拱所在圆的半径为米.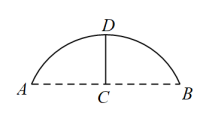 15. 七巧板是我国古代劳动人民的发明之一,被誉为“东方魔板”,它是由五块等腰直角三角形、一块正方形和一块平行四边形共七块板组成的.如图是一个用七巧板拼成的正方形,如果在此正方形中随机取一点,那么此点取自黑色部分的概率是.
15. 七巧板是我国古代劳动人民的发明之一,被誉为“东方魔板”,它是由五块等腰直角三角形、一块正方形和一块平行四边形共七块板组成的.如图是一个用七巧板拼成的正方形,如果在此正方形中随机取一点,那么此点取自黑色部分的概率是.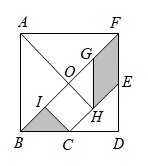 16. 如图,矩形中, , , 点G在边上从F向点E运动,速度为 , 同时点H在边上从E向点D运动,速度为.连接、 , 设、交于点B,取的中点A,则的最小值为.
16. 如图,矩形中, , , 点G在边上从F向点E运动,速度为 , 同时点H在边上从E向点D运动,速度为.连接、 , 设、交于点B,取的中点A,则的最小值为.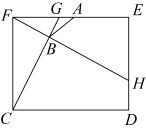
三、解答题
-
17.(1)、计算:(2)、解方程:.18. 已知关于x的一元二次方程有两个实数根.(1)、求k的取值范围;(2)、取一个合适的k的值,使得方程的解为负整数并求出此时方程的解.19. 某学校要调查该校学生(学生总数1200人)双休日的学习状况,采用下列调查方式:①从一个年级里选取200名学生;②选取学校里200名女学生;③按照一定比例在三个不同年级里随机选取200名学生.
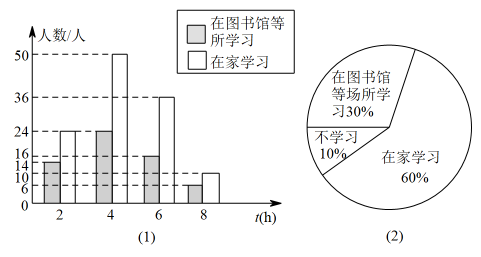 (1)、上述调查方式中最合理的是;(填写序号即可)(2)、将最合理的方式调查得到的数据制成频数分布直方图(如图1)和扇形统计图(如图2),在这个样本中,200名学生双休日在图书馆等场所学习的有人;(3)、在(2)的条件下,请估计该学校1200学生双休日学习时间不少于4小时的人数.20.
(1)、上述调查方式中最合理的是;(填写序号即可)(2)、将最合理的方式调查得到的数据制成频数分布直方图(如图1)和扇形统计图(如图2),在这个样本中,200名学生双休日在图书馆等场所学习的有人;(3)、在(2)的条件下,请估计该学校1200学生双休日学习时间不少于4小时的人数.20.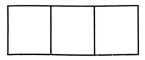 (1)、如图,将“二”“十”“大”三个汉字随机填写在三个空格中(每空填一个汉字,每空中的汉字不重复),请你用画树状图或列表的方法求从左往右汉字顺序恰好是“二十大”的概率;(2)、若在如图三个空格的右侧增加一个空格,将“祖”“国”“你”“好”四个汉字任意填写其中(每空填一个汉字,每空中的汉字不重复),从左往右汉字顺序恰好是“祖国你好”的概率为.21. 如图,在中,E是边的延长线上一点,连接交边于点F,交对角线于点G.
(1)、如图,将“二”“十”“大”三个汉字随机填写在三个空格中(每空填一个汉字,每空中的汉字不重复),请你用画树状图或列表的方法求从左往右汉字顺序恰好是“二十大”的概率;(2)、若在如图三个空格的右侧增加一个空格,将“祖”“国”“你”“好”四个汉字任意填写其中(每空填一个汉字,每空中的汉字不重复),从左往右汉字顺序恰好是“祖国你好”的概率为.21. 如图,在中,E是边的延长线上一点,连接交边于点F,交对角线于点G.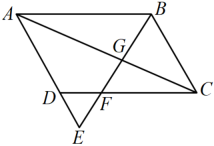 (1)、求证:;(2)、若 , 求的值.22. 如图,点A在的直径的延长线上,点B在上,连接、.
(1)、求证:;(2)、若 , 求的值.22. 如图,点A在的直径的延长线上,点B在上,连接、.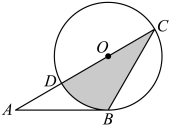 (1)、给出下列信息:①;②;③与相切.
(1)、给出下列信息:①;②;③与相切.请在上述3条信息中选择其中两条作为条件,第三个作为结论,组成一个正确的命题并作出证明.你选择的条件是 , 结论是(填写序号,只需写出你认为正确的一种情形).
(2)、在(1)的条件下,若 , 求图中阴影部分的面积.23. 如图,小明想要利用无人机测量他家附近一座古塔()的高度.在古塔所在的地平面上选定点C.在C处测得古塔顶端A点的仰角为 , 小明遥控无人机悬停在点C正上方的D处时,测得古塔顶端A点的俯角为 , 若此时无人机显示屏上显示其离地面的高度()为.求古塔()的高度以及观测点到古塔的水平距离().(参考数据: , , )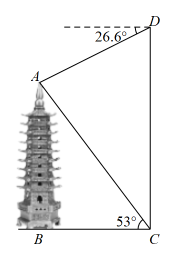 24. 一水果店售卖一种水果,以8元/千克的价格进货,经过往年销售经验可知:以12元/千克售卖,每天可卖60千克;若每千克涨价0.5元,每天要少卖2千克;若每千克降价0.5元,每天要多卖2千克,但不低于成本价.设该商品的价格为x元/千克时,一天销售总质量为y千克.(1)、求y与x的函数关系式.(2)、若水果店货源充足,每天以固定价格x元/千克销售 , 试求出水果店每天利润W与单价x的函数关系式,并求出当x为何值时,利润达到最大.25. 数学兴趣小组在探究圆中图形的性质时,用到了半径是6的若干圆形纸片.
24. 一水果店售卖一种水果,以8元/千克的价格进货,经过往年销售经验可知:以12元/千克售卖,每天可卖60千克;若每千克涨价0.5元,每天要少卖2千克;若每千克降价0.5元,每天要多卖2千克,但不低于成本价.设该商品的价格为x元/千克时,一天销售总质量为y千克.(1)、求y与x的函数关系式.(2)、若水果店货源充足,每天以固定价格x元/千克销售 , 试求出水果店每天利润W与单价x的函数关系式,并求出当x为何值时,利润达到最大.25. 数学兴趣小组在探究圆中图形的性质时,用到了半径是6的若干圆形纸片.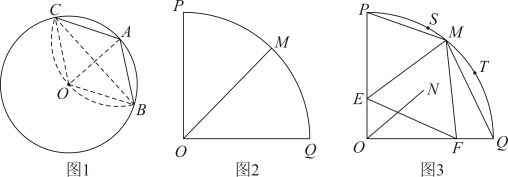 (1)、如图1,一张圆形纸片,圆心为O,圆上有一点A,折叠圆形纸片使得A点落在圆心O上,折痕交于B、C两点,求的度数.(2)、把一张圆形纸片对折再对折后得到如图扇形,点M是弧上一动点.
(1)、如图1,一张圆形纸片,圆心为O,圆上有一点A,折叠圆形纸片使得A点落在圆心O上,折痕交于B、C两点,求的度数.(2)、把一张圆形纸片对折再对折后得到如图扇形,点M是弧上一动点.①如图2,当点M是弧中点时,在线段、上各找一点E、F,使得是等边三角形.试用尺规作出 , 不证明,但简要说明作法 , 保留作图痕迹.
②在①的条件下,取的内心N,则 .
③如图3,当M在弧上三等分点S、T之间(包括S、T两点)运动时,经过兴趣小组探究都可以作出一个是等边三角形,取的内心N,请问的长度是否变化.如变化,请说明理由;如不变,请求出的长度.
26. 阅读材料:小明同学在平面直角坐标系中研究中点时,发现了一个有趣的结论:若 , 是平面直角坐标系内两点,是的中点,则有结论 , .这其实就是中点坐标公式,有了这个公式可以解决很多坐标系中求中点坐标的问题.已知:二次函数的函数图象上分别有A,B两点,其中 , A,B分别在对称轴的异侧,C是中点,D是中点.利用阅读材料解决如下问题:
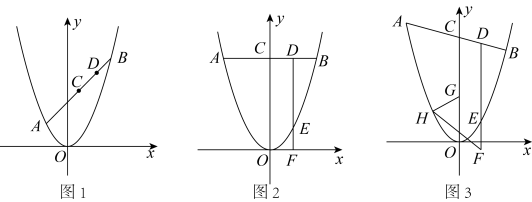 (1)、 概念理解:
(1)、 概念理解:如图1,若 , 求出C,D的坐标.
(2)、 解决问题:如图2,点A是B关于y轴的对称点,作轴交抛物线于点E.延长至F,使得.试判断F是否在x轴上,并说明理由.
(3)、 拓展探究:如图3,是一个动点,作轴交抛物线于点E.延长至F,使得.
①令 , 试探究值是否为定值,若是,求出这个定值;若不是,请说明理由.
②在①条件下,y轴上一点 , 抛物线上任意一点H,连接 , , 直接写出的最小值.