湖南省 湘西土家族苗族自治州凤凰县2022-2023学年九年级上学期期末学情诊断数学试卷
试卷更新日期:2023-03-01 类型:期末考试
一、单选题
-
1. 如图所示的标志中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 已知一元二次方程 , 下列配方正确的是( )A、 B、 C、 D、3. 抛物线y=(x﹣1)2﹣3的对称轴是( )
2. 已知一元二次方程 , 下列配方正确的是( )A、 B、 C、 D、3. 抛物线y=(x﹣1)2﹣3的对称轴是( )
A、y轴 B、直线x=﹣1 C、直线x=1 D、直线x=﹣34. 如图,⊙O是△ABC的外接圆,∠A=50°,则∠BOC的度数为( ) A、40° B、50° C、80° D、100°5. 如图,将△ABC绕点C顺时针旋转90°得到△EDC . 若点A , D , E在同一条直线上,∠ACB=20°,则∠ADC的度数是( )
A、40° B、50° C、80° D、100°5. 如图,将△ABC绕点C顺时针旋转90°得到△EDC . 若点A , D , E在同一条直线上,∠ACB=20°,则∠ADC的度数是( )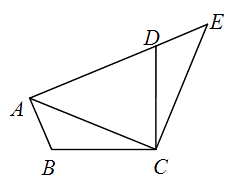 A、55° B、60° C、65° D、70°6. 在平面直角坐标系中,将抛物线y=3x2先向右平移1个单位,再向上平移2个单位,得到的抛物线的解析式是( )
A、55° B、60° C、65° D、70°6. 在平面直角坐标系中,将抛物线y=3x2先向右平移1个单位,再向上平移2个单位,得到的抛物线的解析式是( )
A、y=3(x+1)2+2 B、y=3(x+1)2﹣2 C、y=3(x﹣1)2+2 D、y=3(x﹣1)2﹣27. 在不透明的布袋中装有1个红球,2个白球,3个黑球,它们除颜色外完全相同,从袋中任意摸出一个球,摸出的球是红球的概率是A、 B、 C、 D、8. 如图,⊙O是△ABC的内切圆,则点O是△ABC的( )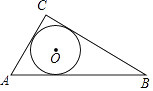 A、三条边的垂直平分线的交点 B、三条角平分线的交点 C、三条中线的交点 D、三条高的交点9. 如图,动点P从点A出发,沿线段AB运动至点B后,立即按原路返回,点P在运动过程中速度大小不变,则以点A为圆心,线段AP长为半径的圆的面积S与点P的运动时间t之间的函数图象大致为( )
A、三条边的垂直平分线的交点 B、三条角平分线的交点 C、三条中线的交点 D、三条高的交点9. 如图,动点P从点A出发,沿线段AB运动至点B后,立即按原路返回,点P在运动过程中速度大小不变,则以点A为圆心,线段AP长为半径的圆的面积S与点P的运动时间t之间的函数图象大致为( ) A、
A、 B、
B、 C、
C、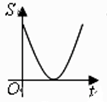 D、
D、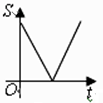 10. 已知二次函数与轴的一个交点为 , 其部分图像如图所示,有下列5个结论:①;②;③;④;⑤ , 其中正确的个数有( )
10. 已知二次函数与轴的一个交点为 , 其部分图像如图所示,有下列5个结论:①;②;③;④;⑤ , 其中正确的个数有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 已知:是关于x的一元二次方程,则m=.12. 三角形两边的长分别是3和4,第三边的长是方程x2-12x+35=0的根,则该三角形的周长为.13. 点关于原点O的对称点的坐标是.14. 抛物线的顶点坐标是.15. 如图,四边形ABCD内接于⊙O,E是BC延长线上一点,若∠BAD=105°,则∠DCE的度数是°.
 16. 在同一坐标系下,抛物线y1=﹣x2+4x和直线y2=2x的图象如图所示,那么不等式-x2+4x>2x的解集是 .
16. 在同一坐标系下,抛物线y1=﹣x2+4x和直线y2=2x的图象如图所示,那么不等式-x2+4x>2x的解集是 .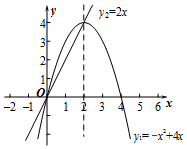 17. 如图,是一个高速公路的隧道的横截面,若它的形状是以O为圆心的圆的一部分,路面米,拱高米,则此圆的半径=.
17. 如图,是一个高速公路的隧道的横截面,若它的形状是以O为圆心的圆的一部分,路面米,拱高米,则此圆的半径=. 18. 如图,已知⊙P的半径是1,圆心P在抛物线上运动,当⊙P与x轴相切时,圆心P的坐标为 .
18. 如图,已知⊙P的半径是1,圆心P在抛物线上运动,当⊙P与x轴相切时,圆心P的坐标为 .
三、解答题
-
19. 用适当的方法解方程3(x-1)2=2(x-1).20. 已知关于x的方程 ,(1)、求证:方程恒有两不等实根;(2)、若x1 , x2是该方程的两个实数根,且 , 求a的值.21. 张师傅今年初开了一家药店,二月份开始盈利,二月份的盈利是6000元,四月份的盈利达到8640元,且从今年二月到四月,每月盈利的平均增长率都相同.(1)、求每月盈利的平均增长率;(2)、按照这个平均增长率,预计今年五月份的盈利能达到多少元?22. 在平面直角坐标系中,△ABC的位置如图所示.(每个小方格都是边长为1个单位长度的正方形)

( 1 )画出△ABC关于原点对称的;
( 2 )将绕点C′顺时针旋转90°,画出旋转后得到的 , 并直接写出此过程中点A′运动的路径长度.(结果保留π)
23. 2022年冬奥会吉祥物为“冰墩墩”,冬残奥会吉祥物为“雪容融”,如图,现有三张正面印有吉祥物的不透明卡片,卡片除正面图案不同外,其余均相同,其中两张正面印有冰墩墩图案的卡片分别记为A1、A2 , 正面印有雪容融图案的卡片记为B,将三张卡片正面向下洗匀,小明同学从中随机抽取一张卡片,记下图案后正面向下放回,洗匀后再从中随机抽取一张卡片. (1)、从这三张卡片中随机挑选一张,是“冰墩墩”的概率是 ;(2)、请用画树状图或列表的方法,求小明同学抽出的两张卡片都是冰墩墩卡片的概率.24. 如图,AB是⊙O的直径, ,E是OB的中点,连接CE并延长到点F,使EF=CE.连接AF交⊙O于点D,连接BD,BF.
(1)、从这三张卡片中随机挑选一张,是“冰墩墩”的概率是 ;(2)、请用画树状图或列表的方法,求小明同学抽出的两张卡片都是冰墩墩卡片的概率.24. 如图,AB是⊙O的直径, ,E是OB的中点,连接CE并延长到点F,使EF=CE.连接AF交⊙O于点D,连接BD,BF. (1)、求证:直线BF是⊙O的切线;(2)、若OB=2,求BD的长.25. 某服装专卖店11月份销售品牌服装,成本价为80元/件,上旬售价是120元/件,每天可卖出20件.市场调查反映:如调整单价,每涨价1元,每天要少卖出1;每降价1元,每天可多卖出2件.调整价格时也要兼顾顾客利益.(1)、若专卖店11月中旬每天获得1200元利润,试求出是如何确定售价的.(2)、假如你是这家服装专卖店的老板,11月下旬你如何确定售价每天获润利最大,并求出最大利润.26. 如图,抛物线y=-x2+bx+c与x轴交于点A(1,0)和点B(-3,0),与y轴交于点C.
(1)、求证:直线BF是⊙O的切线;(2)、若OB=2,求BD的长.25. 某服装专卖店11月份销售品牌服装,成本价为80元/件,上旬售价是120元/件,每天可卖出20件.市场调查反映:如调整单价,每涨价1元,每天要少卖出1;每降价1元,每天可多卖出2件.调整价格时也要兼顾顾客利益.(1)、若专卖店11月中旬每天获得1200元利润,试求出是如何确定售价的.(2)、假如你是这家服装专卖店的老板,11月下旬你如何确定售价每天获润利最大,并求出最大利润.26. 如图,抛物线y=-x2+bx+c与x轴交于点A(1,0)和点B(-3,0),与y轴交于点C. (1)、求b,c的值;(2)、如图1,点P为直线BC上方抛物线上的一个动点,设点P的横坐标m.当m为何值时,△PBC的面积最大?并求出这个面积的最大值.(3)、如图2,将该抛物线向左平移2个单位长度得到新的抛物线y=a1x2+b1x+c1(a1≠0),平移后的抛物线与原抛物线相交于点D,点M为直线BC上的一点,点N是平面坐标系内一点,是否存在点M,N,使以点B,D,M,N为顶点的四边形为菱形,若存在,请直接写出点M的坐标;若不存在,请说明理由.
(1)、求b,c的值;(2)、如图1,点P为直线BC上方抛物线上的一个动点,设点P的横坐标m.当m为何值时,△PBC的面积最大?并求出这个面积的最大值.(3)、如图2,将该抛物线向左平移2个单位长度得到新的抛物线y=a1x2+b1x+c1(a1≠0),平移后的抛物线与原抛物线相交于点D,点M为直线BC上的一点,点N是平面坐标系内一点,是否存在点M,N,使以点B,D,M,N为顶点的四边形为菱形,若存在,请直接写出点M的坐标;若不存在,请说明理由.