湖南省湘西凤凰县2022-2023学年八年级上学期期末学情诊断数学试卷

试卷更新日期：2023-03-01 类型：期末考试

进入出卷网下载

一、单选题

1. 下列四个手机 $A P P$ 图标中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列长度的三条线段，能组成三角形的是（）

A、1，2，3 B、2，3，4 C、2，3，6 D、4，6，10

查看试题解析
3. 下列运算中正确的是（）

A、 $b^{4} • b^{4} = 2 b^{4}$ B、 $(x^{3})^{3} = x^{6}$ C、 $a^{10} \div a^{9} = a$ D、 $(- 3 p q)^{2} = 6 p^{2} q^{2}$

查看试题解析
4. 若等腰三角形的两条边的长分别为3cm和7cm，则它的周长是（）

A、10cm B、13cm C、17cm D、13cm或17cm

查看试题解析
5. 在平面直角坐标系中，已知点 $A (2 ， m)$ 和点 $B (n ， - 3)$ 关于x轴对称，则 $m + n$ 的值是（　　）

A、 $- 1$ B、1 C、 $- 5$ D、5

查看试题解析
6. 下列各式中： $- 3 x$ ， $\frac{5}{x y}$ ， $\frac{6}{π}$ ， $\frac{1}{m}$ ， $\frac{x - 1}{3}$ ，分式的个数是（　　）

A、2 B、3 C、4 D、5

查看试题解析
7. 在 $Δ A B C$ 中，若 $∠ A = 60 ° ， ∠ B = 40 °$ ，则 $∠ C$ 的度数为（）

A、 $40 °$ B、 $60 °$ C、 $80 °$ D、 $100 °$

查看试题解析
8. 下列各式从左到右的变形中，是因式分解且完全正确的是（　　）

A、 $x^{3} - x = x (x^{2} - 1)$ B、 $x^{2} - 2 x - 3 = x (x - 2) - 3$ C、 $x^{2} - 4 x + 4 = {(x - 2)}^{2}$ D、 $(x + 2) (x - 2) = x^{2} - 4$

查看试题解析
9. 如果把分式 $\frac{2 x}{x y}$ 中的x和y都扩大为原来的10倍，那么分式的值（）

A、不变 B、扩大为原来的10倍 C、缩小为原来的 $\frac{1}{10}$ 倍 D、缩小为原来的 $\frac{1}{100}$

查看试题解析
10. 如图，在 $Δ A B C$ 中， $∠ C = 90 °$ ， $A D$ 平分 $∠ C A B$ ，若 $A B = 10$ ， $C D = 3$ ，则 $△ A B D$ 的面积是（　　）

A、9 B、12 C、15 D、24

查看试题解析

二、填空题

11. 三角形的两边长分别是10和8，则第三边的x取值范围是.

查看试题解析
12. 若分式 $\frac{x - 2}{x + 2}$ 的值存在，则x的取值应满足．

查看试题解析
13. 已知等腰三角形的顶角是底角的4倍，则顶角的度数为.

查看试题解析
14. 如图，自行车的主框架采用了三角形结构，这样设计的依据是.

查看试题解析
15. 若多边形的每个外角都为60°，则它的内角和°．

查看试题解析
16. 如图，若要用“HL”证明 $R t △ A B C$ ≌ $R t △ A B D$ ，则需要添加的一个条件是.

查看试题解析
17. 如图，在 $△ A B C ≌ △ E D C$ ，点D落在 $A B$ 上，且 $∠ B = 60 °$ ，则 $∠ E D A =$ .

查看试题解析
18. 如图 $△ A B C$ 中，已知D、E、F分别是BC、AD、CE的中点，且 $S_{△ A B C} = 8$ ，那么阴影部分的面积为.

查看试题解析

三、解答题

19. 因式分解：

(1)、 $m^{2} - 12 m + 36$

(2)、 $a^{3} b - a b^{3}$

查看试题解析
20. 解分式方程： $\frac{2 x}{x + 2} - \frac{x}{x - 1} = 1$ .

查看试题解析
21. 先化简，再求值： $\frac{2 x^{2} - x}{x^{2} - 2 x + 1} \div \frac{2 x - 1}{x - 1} - 1$ ，其中 $x = 3$ .

查看试题解析
22. 如图， $B E = B C ， ∠ A = ∠ D$ .

(1)、求证： $△ A B C ≅ △ D B E$ ；

(2)、求证： $A E = D C$ .

查看试题解析
23. 已知A、B两地相距240千米，甲从A地去B地，乙从B地去A地，甲比乙早出发3小时，两人同时到达目的地.已知乙的速度是甲的速度的2倍.

(1)、甲每小时走多少千米？

(2)、求甲乙相遇时乙走的路程.

查看试题解析
24. 如图，在平面直角坐标系中， $A (2 ， 4) ， B (3 ， 1) ， C (- 2 ， - 1)$ .

(1)、在图中作出 $△ A B C$ 关于x轴对称的图形 $△ A_{1} B_{1} C_{1}$ ；

(2)、写出点 $A_{1} 、 B_{1} 、 C_{1}$ 三点的坐标；

(3)、求 $△ A B C$ 的面积.

查看试题解析
25. 阅读下列材料：
利用完全平方公式，可以将多项式 $a x^{2} + b x + c (a \neq 0)$ 变形为 $a (x + m)^{2} + n$ 的形式，我们把这样的变形方法叫做多项式 $a x^{2} + b x + c$ 的配方法．运用多项式的配方法及平方差公式能对一些多项式进行分解因式．

例如： $x^{2} + 11 x + 24$

＝ $x^{2} + 11 x + (\frac{11}{2})^{2} - (\frac{11}{2})^{2} + 24$

＝ $(x + \frac{11}{2})^{2} - \frac{25}{4}$

＝ $(x + \frac{11}{2} + \frac{5}{2}) (x + \frac{11}{2} - \frac{5}{2})$

＝ $(x + 8) (x + 3)$

根据以上材料，解答下列问题：

(1)、用多项式的配方法将 $x^{2} + 8 x - 1$ 化成 $(x + m)^{2} + n$ 的形式；

(2)、下面是某位同学用配方法及平方差公式把多项式 $x^{2} - 3 x - 40$ 进行分解因式的解答过程：

老师说，这位同学的解答过程中有错误，请你找出该同学解答中开始出现错误的地方，并用“ ”标画出来，然后写出完整的、正确的解答过程：

(3)、求证：x，y取任何实数时，多项式 $x^{2} + y^{2} - 2 x - 4 y + 16$ 的值总为正数．

查看试题解析
26. 如图1，AC＝BC，CD＝CE，∠ACB＝∠DCE＝α，AD、BE相交于点M，连接MC．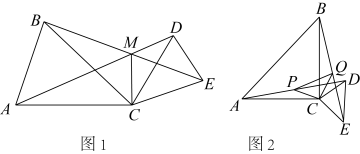

(1)、求证：BE＝AD；

(2)、用含α的式子表示∠AMB的度数（直接写出结果）；

(3)、当 $α = 90 °$ 时，取AD，BE的中点分别为点P、Q，连接CP，CQ，PQ，如图2，判断△CPQ的形状，并加以证明．

查看试题解析