湖南省邵阳市新邵县2022-2023学年九年级上学期期末质量检测数学试题
试卷更新日期:2023-03-01 类型:期末考试
一、单选题
-
1.
利用计算器求tan45°时,依次按键
 则计算器上显示的结果是( )A、0.5 B、0.707 C、0.866 D、12. 方程的解是( )A、 B、 C、 , D、 ,3. 某闭合并联电路中,各支路电流与电阻成反比例,如图表示该电路I与电阻R的函数关系图象,若该电路中某导体电阻为 , 则导体内通过的电流为( )
则计算器上显示的结果是( )A、0.5 B、0.707 C、0.866 D、12. 方程的解是( )A、 B、 C、 , D、 ,3. 某闭合并联电路中,各支路电流与电阻成反比例,如图表示该电路I与电阻R的函数关系图象,若该电路中某导体电阻为 , 则导体内通过的电流为( ) A、 B、 C、 D、4. 我国古代数学名著《九章算术》有“米谷粒分”题;粮仓开仓收粮,有人送来谷米1500石,验得其中夹有谷粒.现从中抽取谷米一把,共数得300粒,其中夹有谷粒30粒,则这批谷米内夹有谷粒约是( )A、150石 B、300石 C、500石 D、1000石5. 如图,D是 边AB上一点,则下列四个条件不能单独判定 的是( )
A、 B、 C、 D、4. 我国古代数学名著《九章算术》有“米谷粒分”题;粮仓开仓收粮,有人送来谷米1500石,验得其中夹有谷粒.现从中抽取谷米一把,共数得300粒,其中夹有谷粒30粒,则这批谷米内夹有谷粒约是( )A、150石 B、300石 C、500石 D、1000石5. 如图,D是 边AB上一点,则下列四个条件不能单独判定 的是( ) A、 B、 C、 D、6. 对于反比例函数.下列说法不正确的是( )A、图象分布在二,四象限内 B、图象经过点 C、当时,y随x的增大而增大 D、若点都在函数的图象上,且时,则7. 如图,A、D、B在同一条直线上,电线杆的高度为h,两根拉线与相互垂直, , 则拉线的长度为( )
A、 B、 C、 D、6. 对于反比例函数.下列说法不正确的是( )A、图象分布在二,四象限内 B、图象经过点 C、当时,y随x的增大而增大 D、若点都在函数的图象上,且时,则7. 如图,A、D、B在同一条直线上,电线杆的高度为h,两根拉线与相互垂直, , 则拉线的长度为( )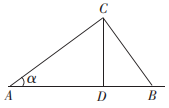 A、 B、 C、 D、8. 如图,五边形与五边形是位似图形,O为位似中心, , 则为( )
A、 B、 C、 D、8. 如图,五边形与五边形是位似图形,O为位似中心, , 则为( ) A、2:3 B、3:2 C、1:2 D、2:19. 现代互联网技术的广泛应用,促进快递行业高速发展,据调查,我市某家快递公司,今年3月份与5月份完成投递的快递总件数分别为6.3万件和8万件.设快递公司这两个月投递总件数的月平均增长率为x,则下列方程正确的是( )A、6.3(1+2x)=8 B、6.3(1+x)=8 C、6.3(1+x)2=8 D、6.3+6.3(1+x)+6.3(1+x)2=810. 大自然是美的设计师,即使是一片小小的树叶,也蕴含着“黄金分割”.如图,P为AB的黄金分割点 , 如果AB的长度为8cm,那么AP的长度是( )cm.
A、2:3 B、3:2 C、1:2 D、2:19. 现代互联网技术的广泛应用,促进快递行业高速发展,据调查,我市某家快递公司,今年3月份与5月份完成投递的快递总件数分别为6.3万件和8万件.设快递公司这两个月投递总件数的月平均增长率为x,则下列方程正确的是( )A、6.3(1+2x)=8 B、6.3(1+x)=8 C、6.3(1+x)2=8 D、6.3+6.3(1+x)+6.3(1+x)2=810. 大自然是美的设计师,即使是一片小小的树叶,也蕴含着“黄金分割”.如图,P为AB的黄金分割点 , 如果AB的长度为8cm,那么AP的长度是( )cm. A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 已知 ,那么 。12. 如图,点A在双曲线y=上,AB⊥y轴于B,S△ABO =3,则k=
 13. 若m是方程的一个根,则代数式的值等于.14. 如图,已知传送带与水平面所成斜坡的坡度 , 如果它把物体送到离地面10米高的地方,那么物体所经过的路程为米.
13. 若m是方程的一个根,则代数式的值等于.14. 如图,已知传送带与水平面所成斜坡的坡度 , 如果它把物体送到离地面10米高的地方,那么物体所经过的路程为米. 15. 李奶奶在某小区弄了一家便利店,供应A,B,C三个品种的食物,由于不同品种的食物保质期不同,为防止食物滞销而变质,李奶奶进货时很着急.小明为了帮助李奶奶解决这一问题,随机统计一周内销售A,B,C三种食物的数量如下表:
15. 李奶奶在某小区弄了一家便利店,供应A,B,C三个品种的食物,由于不同品种的食物保质期不同,为防止食物滞销而变质,李奶奶进货时很着急.小明为了帮助李奶奶解决这一问题,随机统计一周内销售A,B,C三种食物的数量如下表:食物品种
A
B
C
销售数量(件)
15
45
30
根据统计数据,李奶奶进货时A,B,C三种食物的数量的合理的比是.
16. 若△ABC∽△A′B′C′,且 , △ABC的周长为12cm,则△A′B′C′的周长为.17. 已知是一元二次方程的两根,则.18. 如图,在矩形中, , 点E在上,将矩形沿折叠,点D恰好落在边上的点F处,则的值为 .
三、解答题
-
19. 计算.20. 已知:平行四边形的两边 , 的长是关于x的方程的两个实数根.(1)、m为何值时,四边形是菱形?(2)、若的长为3,求的周长.21. 如图,点E为的边延长线上一点,与交于点F,与交于点G.
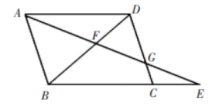 (1)、求证:;(2)、若 , , 求的长度.22. 请你先认真阅读下列材料,再参照例子解答问题:
(1)、求证:;(2)、若 , , 求的长度.22. 请你先认真阅读下列材料,再参照例子解答问题:已知 , 求的值;
解:设 , 则原方程可变形为.即
∴得 ,
∴或
已知 , 求的值.
23. 为了进一步了解某校初中学生的体质健康状况,对九年级的部分学生进行了体质抽测.同时统计了每个人的得分.体质抽测的成绩分为四个等级:优秀、良好、合格 , 不合格根据调查结果绘制了下列两福不完整的统计图,请你根据统计图提供的信息回答以下问题: (1)、补全上面的扇形统计图和条形统计图;(2)、被测试的部分九年级学生的体质测试成绩的中位数落在等级;(3)、若该校九年级有1200名学生,估计该校九年级体质为“不合格”的学生约有多少人?24. 某小区在绿化工程中有一块长为90m、宽为30m的矩形空地,计划在其中修建两块相同的矩形绿地,使它们的面积之和为 , 两块绿地之间及周边留有宽度相等的人行通道(如图所示),求人行通道的宽度.
(1)、补全上面的扇形统计图和条形统计图;(2)、被测试的部分九年级学生的体质测试成绩的中位数落在等级;(3)、若该校九年级有1200名学生,估计该校九年级体质为“不合格”的学生约有多少人?24. 某小区在绿化工程中有一块长为90m、宽为30m的矩形空地,计划在其中修建两块相同的矩形绿地,使它们的面积之和为 , 两块绿地之间及周边留有宽度相等的人行通道(如图所示),求人行通道的宽度.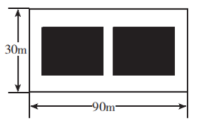 25. 如图,某防洪指挥部发现长江边一处长200米,高10米,背水坡的坡角为的防洪大堤(横断面为梯形)急需加固.经调查论证,防洪指挥部专家组制定的加固方案:沿背水坡面用混泥土进行加固,加固后背水坡的坡比.
25. 如图,某防洪指挥部发现长江边一处长200米,高10米,背水坡的坡角为的防洪大堤(横断面为梯形)急需加固.经调查论证,防洪指挥部专家组制定的加固方案:沿背水坡面用混泥土进行加固,加固后背水坡的坡比. (1)、求加固后坝底增加的宽度;(结果保留根号)(2)、求完成这项工程需要多少方混泥土?(结果精确到1立方米,)26. 如图,反比例函数的图象经过点 , 射线与反比例函数的图象的另一个交点为 , 射线与x轴交于点E,与y轴交于点C,轴,垂足为D.
(1)、求加固后坝底增加的宽度;(结果保留根号)(2)、求完成这项工程需要多少方混泥土?(结果精确到1立方米,)26. 如图,反比例函数的图象经过点 , 射线与反比例函数的图象的另一个交点为 , 射线与x轴交于点E,与y轴交于点C,轴,垂足为D. (1)、求反比例函数的解析式;(2)、求的长;(3)、在x轴上是否存在点P,使得与相似,若存在,请求出满足条件点P的坐标,若不存在,请说明理由.
(1)、求反比例函数的解析式;(2)、求的长;(3)、在x轴上是否存在点P,使得与相似,若存在,请求出满足条件点P的坐标,若不存在,请说明理由.