浙江省绍兴市越城区2022-2023学年九年级上学期期末试卷数学试题（B卷）

试卷更新日期：2023-03-01 类型：期末考试

进入出卷网下载

一、单选题

1. 二次函数 $y = {(x - 2)}^{2} + 1$ 的图象的顶点坐标是（）

A、 $(2 ， - 1)$ B、 $(- 2 ， 1)$ C、 $(2 ， 1)$ D、 $(- 2 ， - 1)$

查看试题解析
2. 已知 $\frac{a}{b} = \frac{2}{3}$ ，则 $\frac{a + b}{b}$ 的值为（）

A、 $\frac{5}{2}$ B、 $\frac{5}{3}$ C、 $\frac{3}{2}$ D、 $\frac{2}{3}$

查看试题解析
3. 观察如图所示的频数直方图，其中组界为99.5~124.5这一组的频数为（）

A、5 B、6 C、7 D、8

查看试题解析
4. 已知直角三角形两条直角边为3，4，则它的外接圆半径为（）

A、1.5 B、2 C、2.5 D、5

查看试题解析
5. 将二次函数y=2x²+1图象向左平移1个单位长度，平移后得到的新函数图象的表达式为（）

A、 $y = 2 x^{2}$ B、 $y = 2 x^{2} + 2$ C、 $y = 2 {(x + 1)}^{2} + 1$ D、 $y = 2 {(x - 1)}^{2} + 1$

查看试题解析
6. 如图，四边形 $A B C D$ 与四边形 $E F G H$ 位似，位似中心点是 $O$ ， $\frac{O E}{E A} = \frac{3}{4}$ ，则 $\frac{F G}{B C}$ 的值为（）

A、 $\frac{3}{4}$ B、 $\frac{4}{3}$ C、 $\frac{3}{7}$ D、 $\frac{4}{7}$

查看试题解析
7. 如图， $A B$ 是 $⊙ O$ 的直径，四边形 $A B C D$ 内接于 $⊙ O$ ，若 $B C = C D = D A = 4$ ，则 $⊙ O$ 的周长为（）

A、 $4 π$ B、 $6 π$ C、 $8 π$ D、 $9 π$

查看试题解析
8. 如图，在 $△ A B C$ 中， $A B = 4 ， A C = 3 ， B C = 5$ .将 $△ A B C$ 沿着点A到点C的方向平移到的 $△ D E F$ 位置，若图中阴影部分面积为2，则 $△ A B C$ 平移的距离为（）

A、2 B、 $\sqrt{2}$ C、 $\sqrt{3}$ D、 $3 - \sqrt{3}$

查看试题解析
9. 如图，点O为正六边形ABCDEF对角线 $F D$ 上一点， $S_{△ A F O} = 4 ， S_{△ C D O} = 1$ ，则 $S_{正六边形 A B C D E F}$ 的值是（）

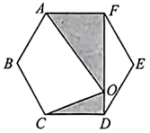A、12 B、15 C、18 D、20

查看试题解析
10. 如图，在平面直角坐标系 $x O y$ 中，⊙O的半径为2，与x轴，y轴的正半轴分别交于点A，B，点C（1，c），D（ $\sqrt{2}$ ， d），E（e，1），P（m，n）均为 $\overset{⌢}{A B}$ 上的点（点P不与点A，B重合），若m＜n＜ $\sqrt{3}$ m，则点P的位置为（）

A、在 $\overset{⌢}{B C}$ 上 B、在 $\overset{⌢}{C D}$ 上 C、在 $\overset{⌢}{D E}$ 上 D、在 $\overset{⌢}{E A}$ 上

查看试题解析

二、填空题

11. 不透明袋子里装有仅颜色不同的 4 个白球和2个红球，从袋子中随机摸出一球，“摸出红球”的概率是．

查看试题解析
12. 已知点P是线段AB的黄金分割点，AP＞PB．若AB＝2，则AP＝．

查看试题解析
13. 二次函数 $y = (x - 1) (x - 3)$ 的最小值是.

查看试题解析
14. 如图， $\overset{⌢}{A B}$ 是半圆，点O为圆心，C、D两点在 $\overset{⌢}{A B}$ 上，且AD∥OC，连接BC、BD．若 $\overset{⌢}{C D}$ ＝65°，则∠ABD的度数为．

查看试题解析
15. 如图，在小正方形边长均为1的 $4 \times 4$ 的网格中， $△ A B C$ 是一个格点三角形.如果 $△ D E F$ ， $△ G H I$ 是该网格中与 $△ A B C$ 相似的格点三角形，且 $△ D E F$ 的面积 $S_{1}$ 最大； $△ G H I$ 的面积 $S_{2}$ 最小，那么 $\frac{S_{1}}{S_{2}}$ 的值等于.

查看试题解析
16. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $s i n B = \frac{3}{5}$ .D是边BC的中点，点E在AB边上，将 $△ B D E$ 沿直线DE翻折，使点B落在同一平面内点F处，线段FD交边AB于点G，若 $F D ⊥ A B$ 时，则 $\frac{A E}{B E} =$ .

查看试题解析

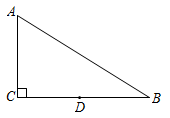
三、解答题

17. 如图，△ABC的高AD，BE交于点F．写出图中所有与△AFE相似的三角形，并选择一个进行证明．

查看试题解析
18. 如图，在平面直角坐标系xOy中，二次函数 $y = x^{2} + b x + c$ 的图象与 $x$ 轴， $y$ 轴的交点分别为 $(1 ， 0)$ 和 $(0 ， - 3)$ ．

(1)、求此二次函数的表达式；

(2)、结合函数图象，直接写出当 $y > - 3$ 时， $x$ 的取值范围．

查看试题解析
19. 已知扇形OAB.

(1)、如图1，请你作一条过圆心O的直线，使扇形的面积被这条直线平分；

(2)、如图2，已知 $O A = \sqrt{2}$ ，若扇形OAB的面积被以O为圆心的 $\overset{⌢}{C D}$ 平分，点C在OA上，点D在OB上，求OC的长，并在图2上作出这条 $\overset{⌢}{C D}$ .
（注：所有作图都要求用尺规作图，不写作法，保留作图痕迹）

查看试题解析
20. 将4张分别写着数字1，2，3，4的卡片（卡片的形状、大小、质地都相同）放在盒子中，搅匀后从中任意取出1张卡片，记录后放回、搅匀，再从中任意取出1张卡片.求下列事件发生的概率.（请选用“画树状图”或“列表”的一种方法写出分析过程）

(1)、取出的2张卡片数字相同；

(2)、取出的2张卡片中，至少有1张卡片数字为“1”.

查看试题解析
21. 如图， $△ A B C$ 内接于⊙O， $A D ∥ B C$ 交⊙O于点D， $D F ∥ A B$ 交 $B C$ 于点E，交⊙O于点F，连接 $A F ， C F$ .

(1)、求证： $A C = A F$ ；

(2)、若⊙O的半径为3， $∠ C A F = 30 °$ ，求 $\overset{⌢}{A C}$ 的长（结果保留π）.

查看试题解析
22. 已知：如图，在△ABC中，点D、E分别在边BC、AC上，点F在DE的延长线上，AD＝AF，AE•CE＝DE•EF．

(1)、求证：△ADE∽△ACD；

(2)、如果AE•BD＝EF•AF，求证：AB＝AC．

查看试题解析
23. 卡塔尔世界杯期间，主办方向中国某企业订购1万幅边长为4米的正方形作品 $A B C D$ ，其设计图案如图所示（四周阴影是四个全等的矩形，用材料甲；中心区是正方形 $A^{'} B^{'} C^{'} D^{'}$ ，用材料乙）.在厚度保持相同的情况下，两种材料的消耗成本如下表

材料

甲

乙

价格（元/米²）

60

30

设矩形的较短边 $A H$ 的长为x米，制作一幅作品的材料费用为y元.

(1)、 $A^{'} D^{'}$ 的长为米（用含x的代数式表示）；

(2)、求y关于x的函数解析式，并写出自变量x的取值范围；

(3)、当中心区的边长不小于3时，预备材料的购买资金700万够用吗？通过运算，请写出你的理由.

查看试题解析
24. 如图，将边长为4的正方形纸片ABCD折叠，使点A落在边CD上的点M处（不与点C、D重合），连接AM，折痕EF分别交AD、BC、AM于点E、F、H，边AB折叠后交边BC于点G．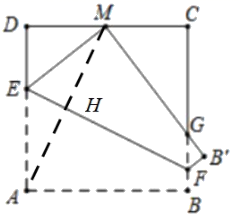

(1)、求证： $△$ EDM∽ $△$ MCG；

(2)、若DM＝ $\frac{1}{3}$ CD，求CG的长；

(3)、若点M是边CD上的动点，四边形CDEF的面积S是否存在最值？若存在，求出这个最值；若不存在，说明理由．

查看试题解析

材料	甲	乙
价格（元/米²）	60	30