浙江省宁波市宁海县2022-2023学年八年级上学期期末抽测数学试卷
试卷更新日期:2023-03-01 类型:期末考试
一、单选题
-
1. 若三角形的两边长分别为 , ,则此三角形第三边的长可能是( )A、 B、 C、 D、2. 用数学的眼光观察下面的网络图标,其中可以抽象成轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 点A(-2,y1),B(3,y2)在一次函数的图象上,y1与y2的大小关系是( )A、 B、 C、 D、4. 若点在第一象限,则点在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 若 , 则一次函数的图象大致是( )A、
3. 点A(-2,y1),B(3,y2)在一次函数的图象上,y1与y2的大小关系是( )A、 B、 C、 D、4. 若点在第一象限,则点在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 若 , 则一次函数的图象大致是( )A、 B、
B、 C、
C、 D、
D、 6. 下列命题的逆命题是假命题的是( )A、直角三角形的两个锐角互余 B、两直线平行,内错角相等 C、三条边对应相等的两个三角形是全等三角形 D、若 , 则7. 如图,在中, , 下列尺规作图,不能得到的是( )A、
6. 下列命题的逆命题是假命题的是( )A、直角三角形的两个锐角互余 B、两直线平行,内错角相等 C、三条边对应相等的两个三角形是全等三角形 D、若 , 则7. 如图,在中, , 下列尺规作图,不能得到的是( )A、 B、
B、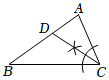 C、
C、 D、
D、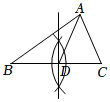 8. 如图,在 中, , , ,点D在AB边上, , ,垂足为F,与BC交于点E,则BE的长是( )
8. 如图,在 中, , , ,点D在AB边上, , ,垂足为F,与BC交于点E,则BE的长是( )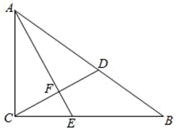 A、3 B、5 C、 D、69. 高斯函数 , 也称为取整函数,即表示不超过的最大整数.例如: , 则下列结论:①;②;③若 , 则的取值范围是;④当时,的值为0,1,2其中正确结论的个数是
A、3 B、5 C、 D、69. 高斯函数 , 也称为取整函数,即表示不超过的最大整数.例如: , 则下列结论:①;②;③若 , 则的取值范围是;④当时,的值为0,1,2其中正确结论的个数是 ( ) A、1 B、2 C、3 D、410. 如图,在中, , , 平分 , , 为边的垂直平分线且分别交、于点、 , 若 , , 则的长是( )
( ) A、1 B、2 C、3 D、410. 如图,在中, , , 平分 , , 为边的垂直平分线且分别交、于点、 , 若 , , 则的长是( )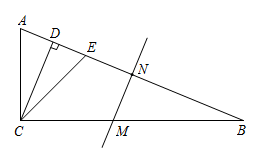 A、2 B、 C、 D、
A、2 B、 C、 D、二、填空题
-
11. 命题“如果 ,则 , ”的逆命题为.12. 如图,若 , 且 , , 则°.
 13. 已知等腰 , 的相邻外角为 , 则这个三角形的顶角为.14. 如图,直线y=x+2与直线y=ax+c相交于点P(m,3).则关于x的不等式x+2≥ax+c的不等式的解为 .
13. 已知等腰 , 的相邻外角为 , 则这个三角形的顶角为.14. 如图,直线y=x+2与直线y=ax+c相交于点P(m,3).则关于x的不等式x+2≥ax+c的不等式的解为 .
 15. 如图,已知反比例函数经过两点,A点坐标 , B点的横坐标为-2,将线段绕点B顺时针旋转90°得到线段 , 则C点坐标为.
15. 如图,已知反比例函数经过两点,A点坐标 , B点的横坐标为-2,将线段绕点B顺时针旋转90°得到线段 , 则C点坐标为. 16. 如图,边长为6的等边三角形中,若点是高所在直线上一点,连接 , 以为边在直线的下方画等边三角形 , 连接 , 则长度的最小值为.
16. 如图,边长为6的等边三角形中,若点是高所在直线上一点,连接 , 以为边在直线的下方画等边三角形 , 连接 , 则长度的最小值为.
三、解答题
-
17. 解不等式组: , 并把不等式组的解集表示在数轴上.
 18. 如图,在方格纸中(每个小正方形的边长均为1个单位长度),有直线和线段 , 其中点 , , , 均在小正方形的顶点上.
18. 如图,在方格纸中(每个小正方形的边长均为1个单位长度),有直线和线段 , 其中点 , , , 均在小正方形的顶点上. (1)、在方格纸中画出线段关于直线的轴对称图形;(2)、若点的坐标为 , 则点的坐标为.19. 如图,点在线段上, , , , 平分.
(1)、在方格纸中画出线段关于直线的轴对称图形;(2)、若点的坐标为 , 则点的坐标为.19. 如图,点在线段上, , , , 平分. (1)、证明:;(2)、若 , , 求的面积.20. 将一副三角板按如图所示的方式叠放在一起,两直角顶点重合于点O.
(1)、证明:;(2)、若 , , 求的面积.20. 将一副三角板按如图所示的方式叠放在一起,两直角顶点重合于点O. (1)、求∠AOD+∠BOC的度数;(2)、当AB的中点E恰好落在CD的中垂线上时,求∠AOC的度数.21. 如图,一次函数 的图象与正比例函数 的图象交于点A(m,2),与y轴的交点为C,与x轴的交点为D.
(1)、求∠AOD+∠BOC的度数;(2)、当AB的中点E恰好落在CD的中垂线上时,求∠AOC的度数.21. 如图,一次函数 的图象与正比例函数 的图象交于点A(m,2),与y轴的交点为C,与x轴的交点为D. (1)、求m的值.(2)、若一次函数图象经过点B(-2,-1),求一次函数的解析式.(3)、在(2)的条件下,求△AOD的面积.22. 某中学为了响应习主席提出的“足球进校园”的号召,开设了“足球大课间活动”,为此购买A种品牌的足球 50个,B种品牌的足球25个,共花费4500元,已知B种品牌足球的单价比A种品牌足球的单价高30元.(1)、求A,B两种品牌足球的单价各多少元?(2)、2019年6月举行“兄弟学校足球联谊赛”活动,根据需要,学校决定再次购进A、B两种品牌的 足球50个,正逢体育用品商店“优惠促销”活动,A种品牌的足球单价优惠4元,B种品牌的足球单价打 8折.如果此次学校购买A、B两种品牌足球的总费用不超过2750元,且购买B种品牌的足球不少于23个,则有几种购买方案?(3)、为了节约资金,学校应选择哪种方案?为什么?23. 定义:在任意中,如果一个内角度数的2倍与另一个内角度数的和为 , 那么称此三角形为“倍角互余三角形”.
(1)、求m的值.(2)、若一次函数图象经过点B(-2,-1),求一次函数的解析式.(3)、在(2)的条件下,求△AOD的面积.22. 某中学为了响应习主席提出的“足球进校园”的号召,开设了“足球大课间活动”,为此购买A种品牌的足球 50个,B种品牌的足球25个,共花费4500元,已知B种品牌足球的单价比A种品牌足球的单价高30元.(1)、求A,B两种品牌足球的单价各多少元?(2)、2019年6月举行“兄弟学校足球联谊赛”活动,根据需要,学校决定再次购进A、B两种品牌的 足球50个,正逢体育用品商店“优惠促销”活动,A种品牌的足球单价优惠4元,B种品牌的足球单价打 8折.如果此次学校购买A、B两种品牌足球的总费用不超过2750元,且购买B种品牌的足球不少于23个,则有几种购买方案?(3)、为了节约资金,学校应选择哪种方案?为什么?23. 定义:在任意中,如果一个内角度数的2倍与另一个内角度数的和为 , 那么称此三角形为“倍角互余三角形”.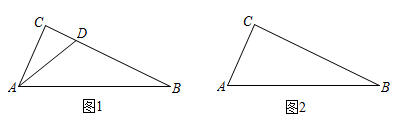 (1)、【基础巩固】若是“倍角互余三角形”, , , 则;(2)、【尝试应用】如图1,在中, , 点为线段上一点,若与互余.求证:是“倍角互余三角形”;(3)、【拓展提高】如图2,在中, , , , 试问在边上是否存在点 , 使得是“倍角互余三角形”?若存在,请求出的长;若不存在,请说明理由.24. 如图,直线与轴交于点 , 直线与轴交于点 , 且经过定点 , 直线与交于点.
(1)、【基础巩固】若是“倍角互余三角形”, , , 则;(2)、【尝试应用】如图1,在中, , 点为线段上一点,若与互余.求证:是“倍角互余三角形”;(3)、【拓展提高】如图2,在中, , , , 试问在边上是否存在点 , 使得是“倍角互余三角形”?若存在,请求出的长;若不存在,请说明理由.24. 如图,直线与轴交于点 , 直线与轴交于点 , 且经过定点 , 直线与交于点. (1)、填空:;;;(2)、在轴上是否存在一点 , 使的周长最短?若存在,请求出点的坐标;若不存在,请说明理由;(3)、若动点在射线上从点开始以每秒1个单位的速度运动,连接 , 设点的运动时间为秒.是否存在的值,使和的面积比为?若存在,直接写出的值;若不存在,请说明理由.
(1)、填空:;;;(2)、在轴上是否存在一点 , 使的周长最短?若存在,请求出点的坐标;若不存在,请说明理由;(3)、若动点在射线上从点开始以每秒1个单位的速度运动,连接 , 设点的运动时间为秒.是否存在的值,使和的面积比为?若存在,直接写出的值;若不存在,请说明理由.