浙江省宁波市南三县2022-2023学年九年级上学期期末质量检测数学
试卷更新日期:2023-03-01 类型:期末考试
一、单选题
-
1. 若一个正n边形的每个外角为30°,则这个正n边形的边数是( )A、10 B、11 C、12 D、142. 如图,在中, , , , 则的值为( )
 A、 B、 C、 D、3. 要将抛物线平移后得到抛物线 , 下列平移方法正确的是( )A、向左平移1个单位,再向上平移3个单位 B、向左平移1个单位,再向下平移3个单位 C、向右平移1个单位,再向上平移3个单位 D、向右平移1个单位,再向下平移3个单位4. 利用六张编号为1,2,3,4,5,6的扑克牌进行频率估计概率的试验中,同学小张统计了某一结果出现的频率,绘出的统计图如图所示,则符合这一结果的试验可能是( )
A、 B、 C、 D、3. 要将抛物线平移后得到抛物线 , 下列平移方法正确的是( )A、向左平移1个单位,再向上平移3个单位 B、向左平移1个单位,再向下平移3个单位 C、向右平移1个单位,再向上平移3个单位 D、向右平移1个单位,再向下平移3个单位4. 利用六张编号为1,2,3,4,5,6的扑克牌进行频率估计概率的试验中,同学小张统计了某一结果出现的频率,绘出的统计图如图所示,则符合这一结果的试验可能是( ) A、抽中的扑克牌编号是3的概率 B、抽中的扑克牌编号是3的倍数的概率 C、抽中的扑克牌编号大于3的概率 D、抽中的扑克牌编号是偶数的概率5. 二次函数的图象与轴有两个交点,则满足的条件是( )A、 B、 C、且 D、6. 如图,在中, , , , 点D在边上, , 以点D为圆心作 , 其半径长为r,要使点A恰在外,点B在内,则r的取值范围是( )
A、抽中的扑克牌编号是3的概率 B、抽中的扑克牌编号是3的倍数的概率 C、抽中的扑克牌编号大于3的概率 D、抽中的扑克牌编号是偶数的概率5. 二次函数的图象与轴有两个交点,则满足的条件是( )A、 B、 C、且 D、6. 如图,在中, , , , 点D在边上, , 以点D为圆心作 , 其半径长为r,要使点A恰在外,点B在内,则r的取值范围是( )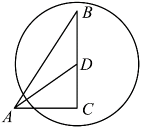 A、 B、 C、 D、7. 如图,在中,点A、B、C在圆上,点D在AB的延长线上,已知 , 则( )
A、 B、 C、 D、7. 如图,在中,点A、B、C在圆上,点D在AB的延长线上,已知 , 则( )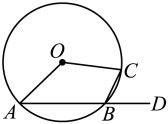 A、 B、 C、 D、8. 如图,在中,对角线 , 交于点 , 为三等分点且 , 连接交于点 , 若的面积为1,则的面积为( )
A、 B、 C、 D、8. 如图,在中,对角线 , 交于点 , 为三等分点且 , 连接交于点 , 若的面积为1,则的面积为( ) A、16 B、20 C、24 D、189. 如图所示为二次函数的图象,对称轴是直线 , 下列结论:;;;;其中正确的个数是( )
A、16 B、20 C、24 D、189. 如图所示为二次函数的图象,对称轴是直线 , 下列结论:;;;;其中正确的个数是( )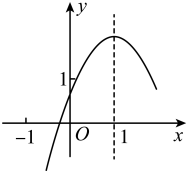 A、1 B、2 C、3 D、410. 如图,在平行四边形中,点分别在边上, , 四边形四边形 , 相似比 , 则下列一定能求出面积的条件( )
A、1 B、2 C、3 D、410. 如图,在平行四边形中,点分别在边上, , 四边形四边形 , 相似比 , 则下列一定能求出面积的条件( ) A、四边形和四边形的面积之差 B、四边形和四边形的面积之差 C、四边形和四边形的面积之差 D、四边形和四边形的面积之差
A、四边形和四边形的面积之差 B、四边形和四边形的面积之差 C、四边形和四边形的面积之差 D、四边形和四边形的面积之差二、填空题
-
11. 若 , 则的值是 .12. 从 , 0, , , -1中任取一个数,取到无理数的概率是.13. 抛物线的顶点坐标是.14. 如图,小明借助太阳光线测量树高.在早上8时小明测得树的影长为 , 下午3时又测得该树的影长为 , 且这两次太阳光线刚好互相垂直,则树高为.
 15. 在圆中,四点在圆上, , , , 则的值为.
15. 在圆中,四点在圆上, , , , 则的值为.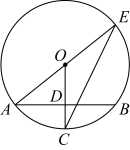 16. 如图,在正方形中,点E在上, , 连接 , 取中点F,过F作且使得 , 连接并延长,将绕点C旋转到 , 当 , , 三点共线且时,.
16. 如图,在正方形中,点E在上, , 连接 , 取中点F,过F作且使得 , 连接并延长,将绕点C旋转到 , 当 , , 三点共线且时,.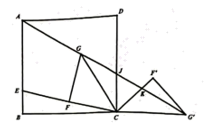
三、解答题
-
17. .18. 如图,在正方形网格中,每个小正方形边长为1,当三角形的三个顶点都在正方形网格线的交点上时,我们称三角形为格点三角形.
 (1)、如图1,请在图1中画一个格点三角形与原三角形相似,且所画三角形与原三角形的相似比为.(2)、请在图2中画一个格点三角形与原三角形相似且有一条公共边,并写出所画三角形与原三角形相似比.相似比为: .19. 随着教育部“双减”政策的深入,某校开发了丰富多彩的课后托管课程,并于开学初进行了学生自主选课活动.小明和小王分别打算从以下四个特色课程选择一个参加:
(1)、如图1,请在图1中画一个格点三角形与原三角形相似,且所画三角形与原三角形的相似比为.(2)、请在图2中画一个格点三角形与原三角形相似且有一条公共边,并写出所画三角形与原三角形相似比.相似比为: .19. 随着教育部“双减”政策的深入,某校开发了丰富多彩的课后托管课程,并于开学初进行了学生自主选课活动.小明和小王分别打算从以下四个特色课程选择一个参加:A.竞技乒乓,B.围棋博弈,C.名著阅读,D.街舞少年.
(1)、小明选择街舞少年的概率为.(2)、用画树状图或列表的方法求小明和小王选择同一个课程的概率.20. 如图1是一个简易手机支架,由水平底板、侧支撑杆和手机托盘长组成,侧面示意图如图2所示.已知手机托盘长 , 侧支撑杆 , , , 其中点A为手机托盘最高点,支撑点B是的中点,手机托盘可绕点B转动,侧支撑杆可绕点D转动. (1)、如图2,求手机托盘最高点A离水平底板的高度h(精确到).(2)、如图3,当手机托盘绕点B逆时针旋转后,再将绕点D顺时针旋转 , 使点C落在水平底板上,求(精确到0.1).(参考数据: , , )21. 生鲜水果店采购了某品牌樱桃,进价每千克50元.而据统计发现樱桃的日销售量(千克)与每千克售价(元)之间满足一次函数关系.(1)、该生鲜水果店要想每日获得1200元的利润,则樱桃的售价每千克应定为多少元?(2)、当每千克樱桃的售价定为多少元时,日销售利润最大?最大利润是多少?22. 如图,在中,以边为直径作分别交 , 于点D,E,点D是中点,连接 , .
(1)、如图2,求手机托盘最高点A离水平底板的高度h(精确到).(2)、如图3,当手机托盘绕点B逆时针旋转后,再将绕点D顺时针旋转 , 使点C落在水平底板上,求(精确到0.1).(参考数据: , , )21. 生鲜水果店采购了某品牌樱桃,进价每千克50元.而据统计发现樱桃的日销售量(千克)与每千克售价(元)之间满足一次函数关系.(1)、该生鲜水果店要想每日获得1200元的利润,则樱桃的售价每千克应定为多少元?(2)、当每千克樱桃的售价定为多少元时,日销售利润最大?最大利润是多少?22. 如图,在中,以边为直径作分别交 , 于点D,E,点D是中点,连接 , . (1)、求证:是等腰三角形.(2)、若 , , 求的长和扇形的面积.23. 已知二次函数的图像经过三点 , , .
(1)、求证:是等腰三角形.(2)、若 , , 求的长和扇形的面积.23. 已知二次函数的图像经过三点 , , . (1)、求二次函数的表达式.(2)、二次函数的图象上若有两点 , 且 , 根据图象直接写出的取值范围.(3)、点是第一象限内二次函数的图象上的一动点,作轴交于点 , 作于点.当点运动时,求面积的最大值.24. 如图1,为圆O的内接三角形,的三条角平分线交于点I,延长AI交圆O于点D,连接.
(1)、求二次函数的表达式.(2)、二次函数的图象上若有两点 , 且 , 根据图象直接写出的取值范围.(3)、点是第一象限内二次函数的图象上的一动点,作轴交于点 , 作于点.当点运动时,求面积的最大值.24. 如图1,为圆O的内接三角形,的三条角平分线交于点I,延长AI交圆O于点D,连接.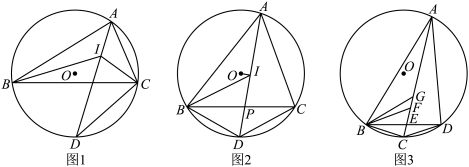 (1)、求证:.(2)、如图2,连接 , 设与交于点P,若 , , 求的长.(3)、如图3,四边形内接于圆O,连接对角线 , 交于点E,且平分 , 过B作交于点F,平分交于点G,若 , , 求的最大值,并求此时圆O的半径.
(1)、求证:.(2)、如图2,连接 , 设与交于点P,若 , , 求的长.(3)、如图3,四边形内接于圆O,连接对角线 , 交于点E,且平分 , 过B作交于点F,平分交于点G,若 , , 求的最大值,并求此时圆O的半径.