浙江省宁波市海曙区2022-2023学年九年级上学期期末质量检测数学试题卷
试卷更新日期:2023-03-01 类型:期末考试
一、单选题
-
1. 下列事件中,是必然事件的是( )A、购买1张彩票,中奖 B、任意画一个三角形,其内角和是180° C、随意翻到一本书的某页,这页的页码是奇数 D、射击运动员射击一次,命中靶心2. 将抛物线先向左平移2个单位,再向下平移1个单位,得到的新抛物线解析式是( )A、 B、 C、 D、3. 如图,点A,B,C,D,E在⊙O上, 的度数为60°,则∠B+∠D的度数是( )
 A、180° B、120° C、100° D、150°4. 如图,在中,分别是、上的点, , 与相交于 , 则下列结论一定正确的是( )
A、180° B、120° C、100° D、150°4. 如图,在中,分别是、上的点, , 与相交于 , 则下列结论一定正确的是( ) A、 B、 C、 D、5. 如图,平面直角坐标系中,点C位于第一象限,点B位于第四象限,四边形是边长为1的正方形,与x轴正半轴的夹角为 , 则点B的纵坐标为( )
A、 B、 C、 D、5. 如图,平面直角坐标系中,点C位于第一象限,点B位于第四象限,四边形是边长为1的正方形,与x轴正半轴的夹角为 , 则点B的纵坐标为( ) A、-2 B、 C、 D、6. 二次函数的部分图象如图所示,当函数值时,x的取值范围是( )
A、-2 B、 C、 D、6. 二次函数的部分图象如图所示,当函数值时,x的取值范围是( ) A、 B、 C、 D、或7. 如图,边长为的小正方形网格中,点在格点上,过三点的圆交于点 , 则的正切值是( )
A、 B、 C、 D、或7. 如图,边长为的小正方形网格中,点在格点上,过三点的圆交于点 , 则的正切值是( ) A、 B、2 C、 D、8. 如图,扇形圆心角为直角, , 点C在上,以 , 为邻边构造 , 边交于点E,若 , 则图中两块阴影部分的面积和为( )
A、 B、2 C、 D、8. 如图,扇形圆心角为直角, , 点C在上,以 , 为邻边构造 , 边交于点E,若 , 则图中两块阴影部分的面积和为( ) A、 B、 C、 D、9. 如图,将含有锐角的三角板绕的锐角顶点C逆时针旋转到 , 、相交于点F,连接 , 若 , 则旋转角的度数为( )
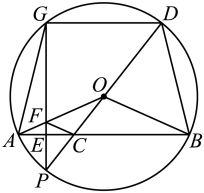
A、 B、 C、 D、9. 如图,将含有锐角的三角板绕的锐角顶点C逆时针旋转到 , 、相交于点F,连接 , 若 , 则旋转角的度数为( ) A、 B、 C、 D、10. 如图,点为的内心,连接并延长交的外接圆于点 , 交于点 , 若 , 则的值为( )
A、 B、 C、 D、10. 如图,点为的内心,连接并延长交的外接圆于点 , 交于点 , 若 , 则的值为( ) A、5 B、6 C、7 D、8
A、5 B、6 C、7 D、8二、填空题
-
11. 从3名男生和2名女生中任选1名学生参加志愿者服务,则选出的这名学生恰好为女生的概率是.12. 若扇形的弧长为 , 圆心角为 , 则该扇形的半径为.13. 如图,在与中, , 连接、 , 若 , 则为.
 14. 已知点在二次函数的图象上,则的最大值等于.15. 如图,的半径为4,为的直径, , 直线与相切于点 , 交的延长线于点 , 若 , 则的长是.
14. 已知点在二次函数的图象上,则的最大值等于.15. 如图,的半径为4,为的直径, , 直线与相切于点 , 交的延长线于点 , 若 , 则的长是. 16. 如图,已知 , 点P、A分别为射线、射线上的动点,将射线绕点P逆时针旋转交射线于点B,则的最大值为.
16. 如图,已知 , 点P、A分别为射线、射线上的动点,将射线绕点P逆时针旋转交射线于点B,则的最大值为.
三、解答题
-
17. 在科学实验复习备考中,王老师为本班学生准备了下面3个实验项目:A.测量物质的密度:B.实验室制取二氧化碳:C探究凸透镜成像.并准备了如图的三等分转盘,规定每名学生可转动一次转盘,并完成转盘停止后指针所指向的实验项目(若指针停在等分线上,则重新转动转盘).根据数学知识回答下列问题:
 (1)、请直接写出:小明同学转动一次转盘,正好选中自己熟悉的“A”实验的概率是;(2)、请你求出小明和小红两名同学各转动一次转盘,都没有选中“C”实验的概率(用树状图或列表法求解).18. 如图1是一台多功能手机支架,图2是其侧面示意图,为地面,支架垂直地面,可分别绕点B,C转动,测量知.当转动到 , 且A、C、D三点共线时,求点A到地面的距离.
(1)、请直接写出:小明同学转动一次转盘,正好选中自己熟悉的“A”实验的概率是;(2)、请你求出小明和小红两名同学各转动一次转盘,都没有选中“C”实验的概率(用树状图或列表法求解).18. 如图1是一台多功能手机支架,图2是其侧面示意图,为地面,支架垂直地面,可分别绕点B,C转动,测量知.当转动到 , 且A、C、D三点共线时,求点A到地面的距离. 19. 如图,在的正方形网格中,点均在格点上,请按要求作图.
19. 如图,在的正方形网格中,点均在格点上,请按要求作图. (1)、在图1中画一个格点 , 使.(2)、在图2中画一条格点线段 , 交于点Q,使.20. 如图,抛物线与x轴交于和两点.
(1)、在图1中画一个格点 , 使.(2)、在图2中画一条格点线段 , 交于点Q,使.20. 如图,抛物线与x轴交于和两点. (1)、求此抛物线的解析式;(2)、过点A的直线与抛物线在第一象限交于点D,若点D的纵坐标为5,请直接写出当时,x的取值范围是.21. 如图,是的直径,是的弦,平分交于点D,过点D作的切线 , 交的延长线于点E,交的延长线于点F.
(1)、求此抛物线的解析式;(2)、过点A的直线与抛物线在第一象限交于点D,若点D的纵坐标为5,请直接写出当时,x的取值范围是.21. 如图,是的直径,是的弦,平分交于点D,过点D作的切线 , 交的延长线于点E,交的延长线于点F. (1)、求证:;(2)、若 , 求的长.22. 某农户生产经销一种农副产品,已知这种产品的成本价为20元/千克.市场调查发现,该产品每天的销售量W(千克)与销售价x(元/千克)有如下关系:.设这种产品每天的销售利润为y(元).(1)、求y与x之间的函数关系式;(2)、当销售价定为多少元时,每天的销售利润最大?最大利润是多少?
(1)、求证:;(2)、若 , 求的长.22. 某农户生产经销一种农副产品,已知这种产品的成本价为20元/千克.市场调查发现,该产品每天的销售量W(千克)与销售价x(元/千克)有如下关系:.设这种产品每天的销售利润为y(元).(1)、求y与x之间的函数关系式;(2)、当销售价定为多少元时,每天的销售利润最大?最大利润是多少?