浙江省金华市武义县2022-2023学年九年级上学期期末数学试题

试卷更新日期：2023-03-01 类型：期末考试

进入出卷网下载

一、单选题

1. 如图，从热气球A看一栋大楼顶部B的仰角是（）

A、 $∠ B A D$ B、 $∠ A C B$ C、 $∠ B A C$ D、 $∠ D A C$

查看试题解析
2. 下面图形中，是直棱柱的表面展开图的是（）

A、 B、 C、 D、

查看试题解析
3. 如图，点A，B，C是⊙O上的点，若 $∠ A C B = 51 °$ ，则 $∠ A O B$ 的度数为（）

A、 $51 °$ B、 $90 °$ C、 $102 °$ D、 $110 °$

查看试题解析
4. 如图， $△ A B C$ 和 $△ D E F$ 是位似三角形， $O D = 3 O A$ ， $△ A B C$ 的面积为2，则 $△ D E F$ 的面积为（）

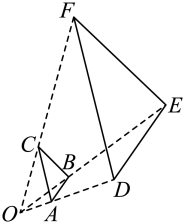A、4 B、6 C、16 D、18

查看试题解析
5. 按小王、小李、小马三位同学的顺序从一个不透明的盒子中随机抽取一张标注“主持人”和两张空白的纸条，确定一位同学主持班级“交通安全教有”主题班会.下列说法中正确的是（）

A、小王的可能性最大 B、小李的可能性最大 C、小马的可能性最大 D、三人的可能性一样大

查看试题解析
6. 若点C是线段AB的黄金分割点， $A C > B C ， A B = 8$ ，则AC的长度为（）

A、 $12 - 4 \sqrt{5}$ B、 $4 \sqrt{5} - 4$ C、5 D、 $2 \sqrt{5}$

查看试题解析
7. 如图，一个蜂巢巢房的横截而为正六边形 $A B C D E F$ ，若对角线 $A D$ 的长约为 $10 m m$ ，则正六边形 $A B C D E F$ 的边长为（）

A、 $4 m m$ B、 $3 \sqrt{2} m m$ C、 $5 m m$ D、 $3 \sqrt{3} m m$

查看试题解析
8. 已知二次函数表达式为 $y = - (x + 2)^{2} - 1$ ，则下列结论中正确的是（）

A、对称轴为直线 $x = 2$ B、最大值是-1 C、顶点坐标为 $(2 ， - 1)$ D、图象开口向上

查看试题解析
9. 图1是一个“不倒翁”，图2是它的主视图， $O A$ ， $O B$ 分别与 $\overset{⌢}{A C B}$ 所在圆相切于点A，B.若该圆半径是8， $∠ O = 54 °$ ，则 $\overset{⌢}{A C B}$ 的长是（）

A、 $2.4 π$ B、 $5.6 π$ C、 $10 π$ D、 $10.4 π$

查看试题解析
10. 如图，二次函数的图象与x轴相交于点A，B，顶点M在矩形 $C D E F$ 的边上移动.若 $C (- 1 ， 1) ， D (3 ， 1) ， E (3 ， 4)$ ，点B的横坐标的最大值为2.5，则点A的横坐标最小值为（）

A、-2 B、 $- \frac{3}{2}$ C、 $- \frac{1}{2}$ D、0

查看试题解析

二、填空题

11. 请写出一个三视图相同的几何体：.

查看试题解析
12. 已知同一时刻物体的高与影子的长成正比例.身高 $1.68 m$ 的小明的影子长为 $0.84 m$ ，这时测得一棵树的影长为 $4 m$ ，则这棵树的高为 $m$ .

查看试题解析
13. 已知抛物线 $y = - x^{2} + 4 x + m$ ，若顶点在x轴上，则 $m =$ .

查看试题解析
14. 如图，在矩形 $A B C D$ 中，点 $E$ 在 $A D$ 上，连接 $C E$ ， $B D$ 相交于点 $F$ ，若 $B C = 4$ ， $\frac{E F}{F C} = \frac{1}{4}$ ，则 $A E$ 的长为.

查看试题解析
15. 如图， $⊙ O$ 的半径 $O D$ 垂直于弦 $A B$ 于点 $C$ ，连结 $A O$ 并延长交 $⊙ O$ 于点 $E$ ，连结 $B E$ .若 $A B = 16 ， C D = 4$ ，则 $B E$ 的长为.

查看试题解析
16. 图1是一种折叠式晾衣架展开时的情况，图2是示意图，两个支脚和晾衣臂 $O A = O B = O C = O D = 6$ ，张开夹角 $∠ A O B = 60 ° ， O E = O F = 2$ ，晾衣臂支架 $E G = F H = 4$ .

(1)、当 $∠ A O D = 90 °$ 时， $∠ E G O$ 的度数为.

(2)、当OC从水平方向旋转到 $O M ⊥ O B$ 时， $△ O N H$ 的面积为.

查看试题解析

三、解答题

17. 计算： $t a n 60 ° + s i n 30 ° - t a n 45 ° \cdot c o s 30 °$ .

查看试题解析
18. 如图，在 $△ A B C$ 中，点 $D ， E ， F$ 分别在边 $A B ， A C ， B C$ 上，连接 $D E ， D F$ .已知 $D E ∥ B C$ ， $D F ∥ A C$ .

(1)、求证： $△ A D E ∼ △ D B F$ .

(2)、若 $\frac{A D}{A B} = \frac{1}{3}$ ， $D E = 3$ ，求 $B F$ 的长.

查看试题解析
19. 如图，小聪全家自驾到某风景区旅游，到达A景点后，导航显示沿北偏西 $60 °$ 方向行驶8千米到达B景点，在B景点查询C景点显示在北偏东 $45 °$ 方向上，到达C景点，小聪发现C景点恰好在A景点的正北方向，求B，C两景点的距离.

查看试题解析
20. 中国古代有若辉煌的数学成就，《周髀算经》《九章算术》《海岛算经》等都是我国古代数学的重要文献.某数学兴趣小组准备采用抽签的方式确定学习内容，将书目制成编号为A，B，C的3张卡片（如图所示，卡片除编号和书目外，其余完全相同）.现将这3张卡片背面朝上，洗匀放好.
A《周脾算经》
B《九章算术》
C《海岛算经》

(1)、从3张卡片中随机抽取1张，求抽到《周髀算经》的概率.

(2)、若从3张卡片中随机抽取2张，请用列表或画树状图的方法，求恰好选中《九章算术》和《海岛算经》的概率.

查看试题解析
21. 如图，小明所在学习兴趣小组在探究“如何测量环形花坛面积（阴影部分）”的方法，准备了下列工具：①卷尺；②直木条（足够长）；③T型尺（EF所在的直线垂直平分线段CD）.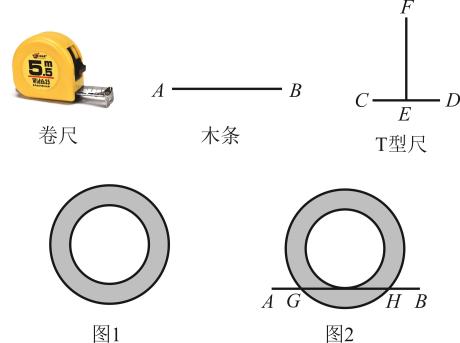

(1)、在图1中，请你用T形尺的原理画出大圆圆心的示意图（保留画图痕迹，不写画法）.

(2)、如图2，小明说：“我只用一根直木条和一个卷尺就可以求出环形花坛的面积，具体做法如下：将直木条放留到与小圆相切，用卷尺量出此时直木条与大圆两交点G，H之间的距离，就可求出环形花坛的面积.”如果测得 $G H = 6 m$ ，请你求出这个环形花坛的面积.

查看试题解析
22. 某农场拟建两间矩形种牛饲养室，饲养室的一面靠已有的墙（墙长大于 $48 m$ ），中间用一道墙隔开，正面开两个门，如图所示，已知每个门的宽度为 $1.5 m$ ，计划中的建筑材料总长 $45 m$ ，设两间饲养室的宽度为 $x m$ ，总占地面积为 $y m^{2}$ .

(1)、求y关于x的函数表达式和自变量x的取值范围.

(2)、求饲养室的宽度为多少 $m$ 时，饲养室最大面积多少 $m^{2}$ ？

(3)、若要使两间饲养室合计占地总面积不低于 $189 m^{2}$ ，求饲养室的宽度 $x m$ 的范围.

查看试题解析
23. 如图1，在菱形 $A B C D$ 中， $A B = 5$ ， $c o s ∠ A B D = \frac{3}{5}$ ，点E从点A出发以每秒1个单位长度沿 $A B$ 运动到点B，然后以同样速度沿 $B C$ 运动到点C停止.设当点E的运动时间为x秒时， $D E$ 长为y.下面是小聪的探究过程，请补充完整.

(1)、根据三角函数值小聪想到连接 $A C$ 交 $B D$ 于点O（如图2），请同学们帮忙求 $B D$ 的长.

(2)、小聪学习了函数知识后，运用函数的研究经验，对y与x的变化规律进行了下列探究，根据点E在 $A B$ 上运动到不同位置进行画图、测量，分别得到了y与x的几组对应值，并画出了函数图象（如图3）：
x
0
1
2
3
4
5
y
5
4.82
4.84
5.06
5.46
6
请同学们继续探究点E在 $B C$ 上的运动情况，在同一坐标系中补全图象，并写出这个函数 $(0 \leq x \leq 10)$ 的两条性质.

(3)、结合图象探究发现 $y = 5$ 时，x有四个不同的值.求y取何值时，x有且仅有两个不同的值.

查看试题解析
24. 如图1，在平面直角坐标系中，O为坐标原点， $△ A B C$ 是等腰直角三角形，点A，点B在x轴上（点A在点B的左侧），点C在y轴的正半轴上，点D在直线BC上运动，连结AD与y轴交于点E，连结BE.

(1)、当点D从点C运动到点B（C，B两点除外）时，求证： $∠ B E O = ∠ C E D$ .

(2)、如图2，过B，D，E三点作⊙H与y轴的另一个交点为G，延长EH交⊙H于点F，连结GF，DG，BF.求 $∠ E F G$ 的度数.

(3)、在（2）的条件下，若 $A B = 8$ ，点D在运动过程中， $△ B E F$ 中是否有一个角等于 $30 °$ ，如果存在，求出此时点E的坐标；如果不存在，请说明理由.

查看试题解析

x	0	1	2	3	4	5
y	5	4.82	4.84	5.06	5.46	6