浙江省金华市武义县2022-2023学年八年级上学期期末数学试题
试卷更新日期:2023-03-01 类型:期末考试
一、单选题
-
1. 一个三角形三个内角的度数之比为1:2:3,则这个三角形一定是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰直角三角形2. 在平面直角坐标系中,将点 向右平移2个单位后,得到的点的坐标是( )A、 B、 C、 D、3. 笔记本每本a元,买3本笔记本共支出y元,下列选项判断正确的有( )A、a是常量时,y是变量 B、a是变量时,y是常量 C、a是变量时,y也是变量 D、无论a是常量还是变量、y都是变量4. 若不等式﹣3x<1,两边同时除以﹣3,得( )A、x>﹣ B、x<﹣ C、x> D、x<5. 对于一次函数 , 下列结论正确的是( )A、函数值随自变量的增大而增大 B、函数的图象经过第三象限 C、函数的图象与轴的交点坐标是 D、函数的图象向下平移4个单位得的图像6. 下列语句中,不是命题的是( )A、两点确定一条直线 B、垂线段最短 C、作角A的平分线 D、内错角相等7. 下列按条件列不等式正确的是( )A、若是非负数,则 B、若的值不大于3,则 C、若与的和小于或等于0,则 D、若的值不小于1,则8. 第十七届省运会在金华隆重举行.一批射击运动员分别乘坐甲乙两辆大巴同时从居住地前往比赛场馆.行驶过程中,大巴甲因故停留一段时间后继续驶向比赛场馆,大巴乙全程匀速驶向比赛场馆.两辆大巴的行程随时间变化的图象(全程)如图所示.依据图中信息,下列说法错误的是( )
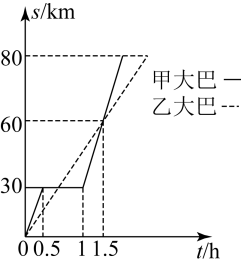 A、大巴甲比大巴乙先到达比赛场馆 B、大巴甲中途停留了 C、大巴甲停留后用追上大巴乙 D、大巴甲停留后的平均速度是9. 在直角坐标系中,已知点 , 点是直线上的两点,则的大小关系是( )A、 B、 C、 D、10. 如图,正方形的边长为 , , , 连结 , 则线段的长为( )
A、大巴甲比大巴乙先到达比赛场馆 B、大巴甲中途停留了 C、大巴甲停留后用追上大巴乙 D、大巴甲停留后的平均速度是9. 在直角坐标系中,已知点 , 点是直线上的两点,则的大小关系是( )A、 B、 C、 D、10. 如图,正方形的边长为 , , , 连结 , 则线段的长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 写出命题“如果 ,那么 互为倒数”的逆命题:.12. 如图,某链条每节长为 , 每两节链条相连接部分重叠的圆的直径为 , 按这种连接方式,x节链条总长度为 , 则y关于x的函数关系式是.
 13. 如图所示的衣架可以近似看成一个等腰三角形ABC,其中 , 底边BC的长 , 那么衣架的高.
13. 如图所示的衣架可以近似看成一个等腰三角形ABC,其中 , 底边BC的长 , 那么衣架的高.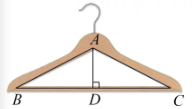 14. 如图,直线与直线交于点 , 由图象可知,不等式的解为.
14. 如图,直线与直线交于点 , 由图象可知,不等式的解为.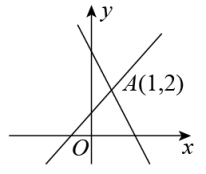 15. 如图,在中,是边上的高,平分 , 交于点E, , 若的面积为9,则的长为.
15. 如图,在中,是边上的高,平分 , 交于点E, , 若的面积为9,则的长为. 16. 如图 , 延长至C,连接.
16. 如图 , 延长至C,连接.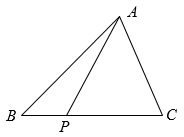 (1)、若 , 则;(2)、若 , 则.
(1)、若 , 则;(2)、若 , 则.三、解答题
-
17. 解不等式(组):(1)、(2)、18. 已知等腰三角形的一边长等于 , 一边长等于 , 求它的周长.19. 王强同学用10块高度都是 的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板( ),点 在 上,点 和 分别与木墙的顶端重合.
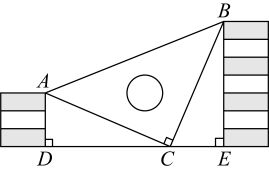 (1)、求证: ;(2)、求两堵木墙之间的距离.20. 如图,在中, , AB的垂直平分线DE分别交AC,AB于点D,E.
(1)、求证: ;(2)、求两堵木墙之间的距离.20. 如图,在中, , AB的垂直平分线DE分别交AC,AB于点D,E.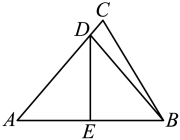 (1)、若 , 求的度数:(2)、若且周长为12,求BC的长.21. 如图,在平面直角坐标系中,已知的三个顶点A,B,C的坐标分别为.
(1)、若 , 求的度数:(2)、若且周长为12,求BC的长.21. 如图,在平面直角坐标系中,已知的三个顶点A,B,C的坐标分别为.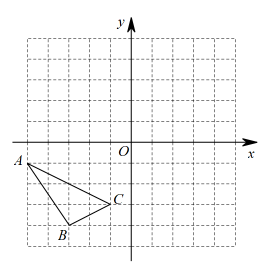 (1)、画出关于y轴对称的;(2)、已知点P在x轴上,且 , 则点P的坐标是;(3)、若y轴上存在点Q,使的周长最小,则点Q的坐标是.22. 非常时期,出门切记戴口罩.当下口罩市场出现热销,某超市老板用1200元购进甲、乙两种型号的口罩在超市俏售,销售完后共获利400元.进价和售价如下表:
(1)、画出关于y轴对称的;(2)、已知点P在x轴上,且 , 则点P的坐标是;(3)、若y轴上存在点Q,使的周长最小,则点Q的坐标是.22. 非常时期,出门切记戴口罩.当下口罩市场出现热销,某超市老板用1200元购进甲、乙两种型号的口罩在超市俏售,销售完后共获利400元.进价和售价如下表:型号
价格
甲型口罩
乙型口罩
进价(元/袋)
2
3
售价(元/袋)
3
3.5
(1)、该超市需购进甲、乙两种型号口罩各多少袋?(2)、该超市第二次又以原来的进价购进甲、乙两种型号口罩共500袋,此次用于购进口罩的资金不少于1220元,但不超过1360元.若两种型号的口罩都按原来的售价全部售完.设此次购进甲种口罩袋,超市获利元,试求关于的函数关系式,并求出的取值范围和超市的最大利润.23. 某游泳池的平面图如图1,宽30米,深水区长40米,浅水区长8米.游泳池应定期换水.图2是小明给游泳池放水时,游泳池的存水量Q(立方米)与放水时间t(小时)的函数图象.其中表示正好放到浅水区底部时的状态.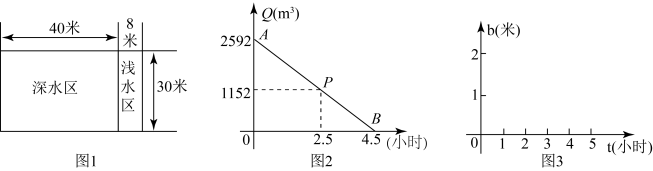 (1)、观察图1,图2.可知:深水区的面积是平方米,浅水区的面积是平方米,放水速度是每小时立方米;(2)、求Q关于t的函数表达式,并写出自变量t的取值范围;(3)、游泳池清理干净后,又将水放到原来的高度.若进水速度与放水速度相同,请在图3中,画出游泳池中的水深h(米)关于进水时间t(小时)的函数图象(请标注关键点的坐标).24. 如图,在平面直角坐标系中,点A在y轴正半轴上,.在第一象限内作等腰 , , .点D为x轴正半轴上的动点,连接AD,将线段AD绕点A逆时针旋转a度,得到线段AE,连接EC并延长交x轴于点F.
(1)、观察图1,图2.可知:深水区的面积是平方米,浅水区的面积是平方米,放水速度是每小时立方米;(2)、求Q关于t的函数表达式,并写出自变量t的取值范围;(3)、游泳池清理干净后,又将水放到原来的高度.若进水速度与放水速度相同,请在图3中,画出游泳池中的水深h(米)关于进水时间t(小时)的函数图象(请标注关键点的坐标).24. 如图,在平面直角坐标系中,点A在y轴正半轴上,.在第一象限内作等腰 , , .点D为x轴正半轴上的动点,连接AD,将线段AD绕点A逆时针旋转a度,得到线段AE,连接EC并延长交x轴于点F. (1)、如图1,当时,线段OF与CF的数量关系是;(2)、如图2,当时,(1)中的结论是否还成立?若成立,请给予证明;若不成立,请说明理由;(3)、若 ,
(1)、如图1,当时,线段OF与CF的数量关系是;(2)、如图2,当时,(1)中的结论是否还成立?若成立,请给予证明;若不成立,请说明理由;(3)、若 ,①求点F的坐标;
②过点E作轴,垂足为P,当是等腰三角形时,求P点的坐标.