浙江省金华市兰溪市2022-2023学年七年级上学期期末检测数学试题

试卷更新日期：2023-03-01 类型：期末考试

进入出卷网下载

一、单选题

1. 比-2大1的数（）

A、-3 B、-1 C、 $- \frac{1}{2}$ D、2

查看试题解析
2. 中国的太空空间站离地球大约400000米，则近似数400000用科学记数法表示为（）

A、 $4 \times 1 0^{4}$ B、 $40 \times 1 0^{4}$ C、 $4 \times 1 0^{5}$ D、 $40 \times 1 0^{5}$

查看试题解析
3. 计算 $5 \div (- 2 - 3)$ 的结果是（）

A、-1 B、 $\frac{1}{5}$ C、 $- \frac{1}{5}$ D、 $- \frac{1}{25}$

查看试题解析
4. 在数 $\frac{1}{7}$ ， $- π$ ， $0.314$ ， $\sqrt{2}$ ， $- \sqrt{64}$ ， 5中，无理数的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 如图是同一时刻北京时间和莫斯科时间.若现在北京时间是x，则同一时刻莫斯科的时间可以表示为（）

A、 $x + 6$ B、 $x - 6$ C、 $x + 5$ D、 $x - 5$

查看试题解析
6. 一个角的补角是它的余角的3倍，则这个角等于（）

A、30° B、45° C、60° D、90°

查看试题解析
7. 我们可以用列方程的方法解决某些数学谜题.如图，小慧同学要猜出“口”中数字，列出可以求解的方程是（）

A、 $12 (460 + x) = 21 (100 x + 64)$ B、 $12 (46 + 10 x) = 21 (100 x + 64)$ C、 $12 (46 + 10 x) = 21 (10 x + 64)$ D、 $12 (460 + x) = 21 (10 x + 64)$

查看试题解析
8. 从杭州东站出发到金华南站的动车，中途要停靠诸暨站和义乌站，则铁路部门供旅客购买的火车票要准备（）

A、12种 B、10种 C、6种 D、4种

查看试题解析
9. 按图示的方法搭1个三角形需要3根火柴棒，搭2个三角形需要5根火柴棒.现有2022根火柴棒，能搭这样的三角形个数为（）

A、1010个 B、1011个 C、1012个 D、1013个

查看试题解析
10. 如图是一个 $3 \times 3$ 在正方形网格，将A、B、C三个棋子放在方格中，规定：每行和每列只能出现一个棋子，则一共的放法有（）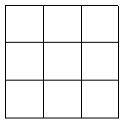

A、18 B、27 C、36 D、48

查看试题解析

二、填空题

11. $- 3$ 的倒数是

查看试题解析
12. 如图是小强与他妈妈的对话，小强说：买笔记本花了 $1.2$ 元……，则小强记不清怎么使用的零花钱有元.

查看试题解析
13. 如图 $3 \times 3$ 方格中，则正方形 $A B C D$ 的边长是 .（方格的边长为1）

查看试题解析
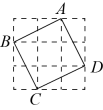14. 如图是一个时钟在 $8 ： 00$ 这个时刻的图形，时针与分针所成的角为度.

查看试题解析
15. 如图所示，一块砖的外墙面积为x，那么图中残缺墙面的面积为.

查看试题解析
16. 一个长方形被分成四个部分的面积分别为 $S_{1}$ ， $S_{2}$ ， $S_{3}$ ， $S_{4}$ .

(1)、如图1，若被两条直线分成四个长方形， $S_{1} = 20$ ， $S_{2} = 25$ ， $S_{3} = 15$ ，则 $S_{4} =$ ；

(2)、如图2，若被条线段分成四个三角形，在① $S_{1}$ 和 $S_{2}$ ， ② $S_{1}$ 和 $S_{3}$ ， ③ $S_{1}$ 和 $S_{4}$ ， ④ $S_{2}$ 和 $S_{4}$ 中，已知则可以求出长方形的面积（填序号）.

查看试题解析

三、解答题

17. 计算：

(1)、 $- 3 + 5 - (- 8)$

(2)、 $\sqrt{9} - 2^{2} \times \frac{1}{4} + \sqrt[3]{- 27} \times | - \frac{1}{3} |$ .

查看试题解析
18. 解方程：

(1)、 $2 (4 - x) = 2 x$ .

(2)、 $\frac{1 + x}{0.1} - \frac{0.4 x - 0.5}{0.2} = \frac{1}{2}$ .

查看试题解析
19. 先化简，再求值： $2 a^{2} b - [2 a b^{2} - 2 (a^{2} b + 2 a b^{2})]$ ，其中 $a = - \frac{1}{2} ， b = 2$ .

查看试题解析
20. 放置在水平地面上两个无盖（朝上的面）的长方体纸盒，大小、形状如图.小长方体的长、宽、高分别为：a（cm）、b（cm）、c（cm）；大长方体的长、宽、高分别为： $1.5 a$ （cm）、 $2 b$ （cm）、 $2 c$ （cm）.

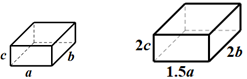(1)、做这两个纸盒共需要材料多少平分厘米？

(2)、做一个大的纸盒比做一个小的纸盒多多少平分厘米材料

查看试题解析
21. 如图1，已知 $∠ B O C = 40 °$ ， $O E$ 平分 $∠ A O C$ ， $O F$ 平分 $∠ B O C$ .

(1)、若 $A O ⊥ B O$ ，则 $∠ E O F$ 是多少度？

(2)、如图2，若角平分线 $O E$ 的位置在射线 $O B$ 和射线 $O F$ 之间（包括重合），请说明 $∠ A O C$ 的度数应控制在什么范围.

查看试题解析
22. 如图，线段 $A B$ 的中点O是数轴原点，点C在点O右侧，分线段 $A B$ 的长度为 $3 ： 2$ ，且 $O C = 3$ .

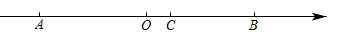(1)、求点A在数轴上代表的数是什么？请说明理由.

(2)、若点P从点C出发，以3个单位/秒的速度向点A运动，到点A停止；点Q从点O出发，以1个单位/秒速度向点B运动，到点B后停止.问运动时间t为几秒时， $P A = Q B$ ？

查看试题解析
23. 小明爸爸在一家电信公司了解到两种移动电话计费方法：计费方法A是每月收月租费30元，通话时间120分钟内免费，超过120分的部分按每分钟0.25元加收通话费；计费方法B是每月收月租费50元，通话时间200分钟内免费，超过200分的部分按每分钟0.2元收通话费.

(1)、若小明爸爸一个月的通话时间大约在150分钟和160分钟之间，请通过计算说明选用哪种计费方式，可以节省费用？

(2)、小明爸爸当前选择了计费方式A，有一个月累计通话240分钟，话费m元.若改成用计费方法B，则同样话费m元，可多通话多少分钟？

(3)、从节省话费的角度考虑，帮小明爸爸选择合适的计费方式.

查看试题解析
24. 问题提出：
如图1，A、B、C、D表示四个村庄，村民们准备合打一口水井.

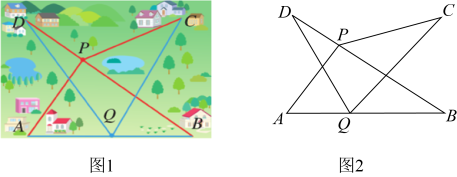(1)、问题解决：
若水井的位置现有P、Q两种选择方案.点P在线段 $B D$ 上，点Q在线段 $A B$ 上，哪一种方案的水井到各村庄的距离总和较小？请说明你判断的理由.

(2)、你能给出一种使水井到各村庄的距离之和最小的方案吗？若能，请图2中标出水井的位置点M，并说明理由.

(3)、问题拓展：
如果（2）问中找出的水井经过招标，由两个工程队修建（不存在同时修建）. 已知甲工程队单独完成需要80天，乙工程队单独完成需要120天，且甲工程队比乙工程队每天多修建 $0.5 m$ .
问水井要修建几米？

(4)、若甲工程队每天的施工费为0.5万元，乙工程队每天的费用是0.25万元，为了缩短工期和节约资金，则甲工程队最多施工几天才能使工程款不超过35万元？（甲、乙两队的施工时间不足一天按一天算）.

查看试题解析