浙江省湖州市长兴县2022-2023学年八年级上学期期末检测数学试题
试卷更新日期:2023-03-01 类型:期末考试
一、单选题
-
1. 下列图形中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 在平面直角坐标系中,点位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 三角形的两边长分别为和 , 此三角形第三边长可能是( )A、 B、 C、 D、4. 如图所示,在数轴上表示不等式正确的是( )
2. 在平面直角坐标系中,点位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 三角形的两边长分别为和 , 此三角形第三边长可能是( )A、 B、 C、 D、4. 如图所示,在数轴上表示不等式正确的是( ) A、 B、 C、 D、5. 对于命题“如果 , 那么”,下面四组关于a,b的值中,能说明这个命题是假命题的是( )A、 , B、 , C、 , D、 ,6. 已知点和点在直线上,且 , 则a的值可能是( )A、-3 B、-2 C、1 D、37. 如图,在中, , 点D是边的中点,若 , 则的度数为( )
A、 B、 C、 D、5. 对于命题“如果 , 那么”,下面四组关于a,b的值中,能说明这个命题是假命题的是( )A、 , B、 , C、 , D、 ,6. 已知点和点在直线上,且 , 则a的值可能是( )A、-3 B、-2 C、1 D、37. 如图,在中, , 点D是边的中点,若 , 则的度数为( ) A、 B、 C、 D、8. 已知 , 且 , 则一次函数的图像大致是( )A、
A、 B、 C、 D、8. 已知 , 且 , 则一次函数的图像大致是( )A、 B、
B、 C、
C、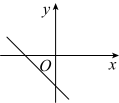 D、
D、 9. 如图,在中, , 分别以A,C为圆心,大于长为半径作弧,两弧相交于点M,N,作直线 , 与 , 分别交于D,E,连接 , 若 , , 则的周长为( )
9. 如图,在中, , 分别以A,C为圆心,大于长为半径作弧,两弧相交于点M,N,作直线 , 与 , 分别交于D,E,连接 , 若 , , 则的周长为( ) A、16 B、17 C、18 D、1910. 如图,在平面直角坐标系中,直线与x轴交于点A,与y轴交于点B,直线与x轴交于点C,与y轴交于点B,若线段上的点D到直线的距离长为3,则点D的坐标为( )
A、16 B、17 C、18 D、1910. 如图,在平面直角坐标系中,直线与x轴交于点A,与y轴交于点B,直线与x轴交于点C,与y轴交于点B,若线段上的点D到直线的距离长为3,则点D的坐标为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
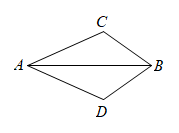
11. 若点与点关于y轴对称,则a的值为 .12. 如果a<b,那么﹣3a﹣3b(用“>”或“<”填空).13. 如图,已知 , 要使 , 还需添加一个条件,这个条件可以是.(写出一个即可)
 14. 已知,如图直线与直线交于点,则不等式的解集为 .
14. 已知,如图直线与直线交于点,则不等式的解集为 . 15. 如图,是直角三角形, , 分别以、为边向两侧作正方形.若图中两个正方形的面积和 , 则.
15. 如图,是直角三角形, , 分别以、为边向两侧作正方形.若图中两个正方形的面积和 , 则. 16. 如图,在中, , , 分别以 , 为边向外作正和正 , 连接 , , 当的边变化过程中,取最长时,则的长为.
16. 如图,在中, , , 分别以 , 为边向外作正和正 , 连接 , , 当的边变化过程中,取最长时,则的长为.
三、解答题
-
17. 解下列不等式(组):(1)、;(2)、.18. 已知y是x的一次函数,且当时,;当时,.(1)、求这个一次函数的表达式;(2)、当时,求出对应y的值.19. 如图, , , , 点E在线段上.
 (1)、求证:;(2)、求的度数.20. 如图,在平面直角坐标系中,的三个顶点的坐标分别为 , , .
(1)、求证:;(2)、求的度数.20. 如图,在平面直角坐标系中,的三个顶点的坐标分别为 , , .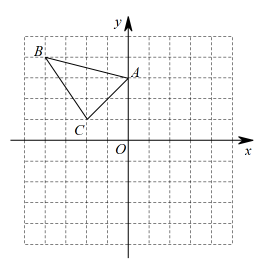 (1)、在图中作出关于原点的对称图形;(2)、请直接写出 , , 的坐标: ; ; .21. 如图,在中, , 平分交于点D,作于点E.
(1)、在图中作出关于原点的对称图形;(2)、请直接写出 , , 的坐标: ; ; .21. 如图,在中, , 平分交于点D,作于点E. (1)、若 , 求的度数;(2)、若 , , 求的面积.22. 为提升学生的文学素养,培养学生的阅读兴趣,某校准备购进A,B两种图书.经调查,购进A种图书费用y元与购进A种图书本数x之间的函数关系如图所示,B种图书每本20元.
(1)、若 , 求的度数;(2)、若 , , 求的面积.22. 为提升学生的文学素养,培养学生的阅读兴趣,某校准备购进A,B两种图书.经调查,购进A种图书费用y元与购进A种图书本数x之间的函数关系如图所示,B种图书每本20元.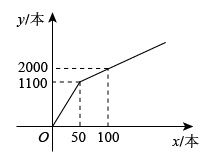 (1)、当和时,求y与x之间的函数关系式;(2)、现学校准备购进300本图书,其中购进A种图书x本,设购进两种图书的总费用为w元.
(1)、当和时,求y与x之间的函数关系式;(2)、现学校准备购进300本图书,其中购进A种图书x本,设购进两种图书的总费用为w元.①当时,求出w与x间的函数表达式;
②若购进A种图书不少于60本,且不超过B种图书本数的2倍,那么应该怎样分配购买A,B两种图书才能使总费用最少?最少总费用多少元?
23. 【问题背景】 (1)、如图1,点P是线段 , 的中点,求证:;(2)、【变式迁移】
(1)、如图1,点P是线段 , 的中点,求证:;(2)、【变式迁移】
如图2,在等腰中,是底边上的高线,点E为内一点,连接 , 延长到点F,使 , 连接 , 若 , 若 , , 求的长;(3)、【拓展创新】
如图3,在等腰中, , , 点D为中点,点E在线段上(点E不与点B,点D重合),连接 , 过点A作 , 连接 , 若 , , 请直接写出的长.24. 如图1,在平面直角坐标系中,直线与x轴交于点A,与y轴交于点B,并与直线相交于点C. (1)、求点C的坐标;(2)、如图2,点D在点C右侧的x轴上,过点D作x轴的垂线与直线交于点E,与直线交于点F,且.
(1)、求点C的坐标;(2)、如图2,点D在点C右侧的x轴上,过点D作x轴的垂线与直线交于点E,与直线交于点F,且.①求点E的坐标;
②若点M是射线上的动点,连接 , 并在左侧作等腰直角 , 当顶点P恰好落在直线上时,求出对应的点M的坐标.