浙江省湖州市吴兴区2022-2023学年九年级上学期数学期末试卷

试卷更新日期：2023-03-01 类型：期末考试

进入出卷网下载

一、单选题

1. 已知 $\frac{a}{b} = \frac{2}{5}$ ，则 $\frac{a}{a + b} =$ （）

A、 $\frac{2}{5}$ B、 $\frac{3}{5}$ C、 $\frac{2}{7}$ D、 $\frac{3}{7}$

查看试题解析
2. 一个不透明的布袋中装有1个白球和2个红球，它们除颜色不同以外其他都相同，从布袋中任意摸出一个球是白球的概率为（）

A、 $\frac{1}{3}$ B、 $\frac{1}{2}$ C、 $\frac{2}{3}$ D、1

查看试题解析
3. 如图，点A、B、C在⊙O上，∠BAC＝56°，则∠BOC的度数为（）

A、28° B、102° C、112° D、128°

查看试题解析
4. 如图，在Rt $△ A B C$ 中， $∠ C = 90 ° ， c o s A = \frac{1}{3}$ ，则 $s i n B$ 的值为（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{2 \sqrt{2}}{3}$ D、 $2 \sqrt{2}$

查看试题解析
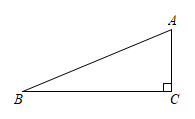5. 将抛物线y＝2（x﹣3）²+1向左平移2个单位长度，再向下平移3个单位长度，则平移后抛物线的顶点坐标是（）

A、（5，4） B、（1，﹣2） C、（﹣1，﹣2） D、（﹣5，﹣2）

查看试题解析
6. 如图， $l_{1} ∥ l_{2} ∥ l_{3}$ ，直线 $a ， b$ 与 $l_{1}$ ， $l_{2}$ ， $l_{3}$ 分别交于点 $A ， B ， C$ 和点 $D ， E ， F$ ，若 $A B ： B C = 2 ： 3$ ， $E F = 15$ ，则DE的长是（）

A、8 B、6 C、4 D、10

查看试题解析
7. 已知点 $A (- 1 ， y_{1})$ ， $B (- 2 ， y_{2})$ ， $C (- 4 ， y_{3})$ 在抛物线 $y = 2 x^{2} + 8 x - 1$ 上，则 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小关系是（）

A、 $y_{1} < y_{2} < y_{3}$ B、 $y_{3} < y_{2} < y_{1}$ C、 $y_{2} < y_{3} < y_{1}$ D、 $y_{2} < y_{1} < y_{3}$

查看试题解析
8. 宽与长的比是 $\frac{\sqrt{5} - 1}{2}$ （约0.618）的矩形叫做黄金矩形，黄金矩形蕴藏着丰富的美学价值，给我们以协调和匀称的美感．我们可以用这样的方法画出黄金矩形：作正方形ABCD，分别取AD、BC的中点E、F，连接EF：以点F为圆心，以FD为半径画弧，交BC的延长线于点G；作GH⊥AD，交AD的延长线于点H，则图中下列矩形是黄金矩形的是（　　）

A、矩形ABFE B、矩形EFCD C、矩形EFGH D、矩形DCGH

查看试题解析
9. 常用水笔的笔尖是通过顶端的球座口内置一颗可以滚动带墨出水的球珠构成（轴截面如图所示），某工厂生产了一批直径均为 $0.5 m m$ 的球珠和可以放置球珠的笔尖，要求笔头球珠探出部分的长度h不少于 $0.05 m m$ 但不超过 $0.1 m m$ ，以下生产的不同球座口宽度a中符合要求的是（）

A、0.45 B、0.35 C、0.25 D、0.15

查看试题解析
10. 如图，在正方形 $A B C D$ 中，以边 $A B$ 为直径在其内部作半圆，F是半圆上一点，连接 $A F$ ， $t a n ∠ B A F = \frac{\sqrt{3}}{2}$ ，过点D作 $D E ⊥ A F$ 于点E，点G是线段ED上一点， $E G = E F$ ，连接 $G F$ 并延长交 $B C$ 于点P，则 $\frac{C P}{B P}$ 的值是（）

A、 $\frac{\sqrt{3}}{3}$ B、 $\frac{2 \sqrt{3}}{3}$ C、 $\sqrt{3}$ D、 $- \frac{\sqrt{3}}{3}$

查看试题解析

二、填空题

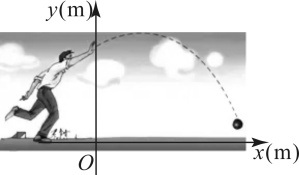
11. 已知 $⊙ O$ 的半径为 $4 c m$ ，点 $P$ 到圆心 $O$ 的距离为 $3 c m$ ，则点 $P$ 在 $⊙ O$ （填内、上、外）.

查看试题解析
12. 圆柱的底面半径为 $1 c m$ ，母线长为 $5 c m$ ，则该圆柱的侧面积为 $c m^{2}$ .

查看试题解析
13. 教练对小明推铅球的录像进行技术分析，建立平面直角坐标系（如图），发现铅球与地面的高度 $y (m)$ 和运动员出手点的水平距离 $x (m)$ 之间的函数关系为 $y = - \frac{1}{10} x^{2} + \frac{4}{5} x + 2$ ，由此可知铅球的落地点与运动员出手点的水平距离是m.

查看试题解析
14. 如图，已知二次函数 $y = a x^{2} + b x + c (a < 0)$ 与一次函数 $y = k x + 1 (k > 0)$ 的图象交于 $A (- 3 ， m)$ ， $B (1 ， n)$ 两点，则关于x的不等式 $a x^{2} + b x + c > k x + 1$ 的解集为.

查看试题解析
15. 如图，已知正六边形 $A B C D E F$ 内接于半径为2的 $⊙ O$ ，点 $M$ ， $N$ 分别是 $A F$ ， $C D$ 的中点，连结 $M B$ ， $B N$ ， $B D$ ， $D F$ ， $N E$ ， $E M$ ，则图中阴影部分的面积为.

查看试题解析
16. 将一组完全一样的宽 $1 c m$ ，高 $5 c m$ 的多米诺骨牌按图1所示垂直放置在地面上，推动至其全部倒下，最后三块骨牌的位置如图2所示.其中①号骨牌水平倒在地面上，已知②号骨牌与地面夹角 $α$ 的正切值为 $\frac{1}{2}$ .

(1)、求 $D F$ 的长为cm.

(2)、若③号骨牌与地面的夹角 $β$ 的正切值为 $\frac{1}{3}$ ，则 $B D$ 的长为cm.

查看试题解析

三、解答题

17. 计算： $2 c o s 60 ° - \sqrt{2} s i n 45 °$ .

查看试题解析
18. 北京将于2022年举办冬奥会和冬残奥会，中国将成为一个举办过五次各类奥林匹克运动会的国家小亮是个集邮爱好者，他收集了如下图所示的四张纪念邮票（除正面内容不同外，其余均相同），现将四张邮票背面朝上，洗匀放好．

(1)、小亮从中随机抽取一张邮票是“冬残奥会吉祥物雪容融”的概率是；

(2)、小亮从中随机抽取一张邮票（不放回），再从余下的邮票中随机抽取一张，请你用列表或画树状图的方法求抽到的两张邮票恰好是“冬奥会会徽”和“冬奥会吉祥物冰墩墩”的概率．（这四张邮票依次分别用字母A，B，C，D表示）

查看试题解析
19. 如图，在平面直角坐标系xOy中，一次函数y=x的图象与二次函数y=-x2+bx（b为常数）的图象相交于O，A两点，点A坐标为（3，m）.

(1)、求m的值以及二次函数的表达式；

(2)、若点P为抛物线的顶点，连结OP，AP，求△POA的面积.

查看试题解析
20. 某小区门口安装了汽车出入道闸.道闸关闭时，如图1，四边形 $A B C D$ 为矩形， $A B$ 长3米， $A D$ 长1米，点 $C$ 与点 $N$ 重合.道闸打开的过程中，边 $A D$ 固定，连杆 $A B$ ， $C D$ 分别绕点 $A$ ， $B$ 转动，且边 $B C$ 始终与边 $A D$ 平行.

(1)、如图2，当道闸打开至 $∠ A D C = 45 °$ 时，边 $C D$ 上一点 $P$ 到地面的距离PE为1米，求点 $P$ 到 $M N$ 的距离 $P F$ 的长.

(2)、一辆轿车过道闸，已知轿车宽1.8米，高1.6米.当道闸打开至 $∠ A D C = 36 °$ 时，轿车能否驶入小区？请说明理由，（参考数据： $s i n 36 ° \approx 0.59$ ， $c o s 36 ° \approx 0.81$ ， $t a n 36 ° \approx 0.73$ ）

查看试题解析
21. 如图， $⊙ O$ 是 $△ A B C$ 的外接圆， $A B = B C$ ， $A D ⊥ B C$ 于点D， $B O$ 的延长线分别交 $A C ， A D$ 于点E、F.

(1)、求证： $∠ C A D = ∠ A B E$ .

(2)、若 $E F = 1$ ， $B F = 3$ ，求AC的长.

查看试题解析
22. “中国元素”几乎遍布卡塔尔世界杯的每一个角落，某特许商品专卖店销售中国制造的纪念品，深受大家喜爱.自世界杯开赛以来，其销量不断增加，该商品销售第x天（ $1 \leq x \leq 28$ ，且x为整数）与该天销售量y（件）之间满足函数关系如下表所示：
第x天
1
2
3
4
5
6
7
…
销售量y（件）
220
240
260
280
300
320
340
…
为回馈项客，该商家将此纪念品的价格不断下调，其销售单价z（元）与第x天（ $1 \leq x \leq 28$ ，且x为整数）成一次函数关系，当 $x = 1$ 时， $z = 98$ ，当 $x = 2$ 时， $z = 96$ .已知该纪念品成本价为20元/件.

(1)、求y关于x的函数表达式，及z与x之间的函数关系式；

(2)、求这28天中第几天销售利润最大，并求出最大利润；

(3)、商店担心随着世界杯的结束该纪念品的销售情况会不如从前，决定在第20天开始每件商品的单价在原来价格变化的基础上再降价a元销售，销售第x天与该天销售量y（件）仍然满足原来函数关系，问第几天的销售利润取得最大值，若最大利润是20250元，求a的值.

查看试题解析
23. 已知在矩形 $A B C D$ 中， $A B = 2$ ， $A D = k A B$ ，点 $E$ 是 $A B$ 边上的一个动点，以 $C E$ 为边，在 $C E$ 的右侧作矩形 $C E F G$ ，且 $C E = k C G$ ，连接 $D G$ ， $B E$ .

(1)、如图1，若 $k = 1$ ，点 $E$ 运动到 $A D$ 的中点时，求 $D G$ 的长.

(2)、如图2，判断 $D G$ 与 $B E$ 有怎样的数量关系，并说明理由.

(3)、当点 $E$ 从点 $A$ 运动到点 $D$ 时，请直接写出点 $G$ 的运动路径长.

查看试题解析
24. 已知抛物线 $y = x^{2} + m x - 2$ 与x轴交于A、B两点，与y轴交于点C，点A坐标为 $(- 2 ， 0)$

(1)、求抛物线的解析式及B、C两点的坐标.

(2)、若点M是线段 $A C$ 上一个动点（不与A、C重合），点N是线段 $A B$ 上一个动点，设 $A N = t (t > 0)$
①如图1，当点N运动到 $A B$ 的中点时，作 $M N ∥ y$ 轴交 $A C$ 于点M.求证： $∠ B M N = ∠ B A C$ .
②如图2，当点N在运动过程中，点M总存在两个不同的位置使 $∠ B M N = ∠ B A C$ ，求出t的范围.
③当点N在运动过程中，在x轴上方的抛物线上是否存在点G，使得 $∠ G N B = ∠ B A C$ 且 $G N$ 恰好平分 $∠ A G B$ ？若存在，求出此时点G的横坐标和t的值；若不存在，请说明理由.

查看试题解析

第x天	1	2	3	4	5	6	7	…
销售量y（件）	220	240	260	280	300	320	340	…