浙江宁波市慈溪市2022-2023学年八年级上学期数学期末卷

试卷更新日期：2023-03-01 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各组线段中，能构成三角形的是（）

A、2，5，7 B、9，3，5 C、4，5，6 D、4，5，10

查看试题解析
2. 在下列交通标志中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 根据下列表述，不能确定具体位置的是（）

A、某电影院1号厅的3排4座 B、慈溪市孙塘北路824号 C、某灯塔南偏西30°方向 D、东经108°，北纬53°

查看试题解析
4. 下列各点一定在函数 $y = 2 x + 1$ 的图象上的是（）

A、 $(2 ， 0)$ B、 $(0 ， 1)$ C、 $(1 ， 0)$ D、 $(- 1 ， 0)$

查看试题解析
5. 在下列各原命题中，逆命题是真命题的是（）

A、直角三角形两个锐角互余 B、对顶角相等 C、全等三角形对应角相等 D、全等的两个三角形面积相等

查看试题解析
6. 下列说法不一定成立的是（）

A、若a>b，则a+c>b+c B、若a+c>b+c，则a>b C、若a>b，则ac²>bc² D、若ac²>bc² ，则a>b

查看试题解析
7. 如图，已知 $△ A B C$ ，小慧同学利用尺规作出 $△ A_{1} B_{1} C_{1}$ 与 $△ A B C$ 全等，根据作图痕迹请判断小慧同学的全等判定依据（）

A、SSS B、SAS C、AAS D、ASA

查看试题解析
8. 看一次函数y=（3-k）x-k的图象经过第一、三、四象限，则k的取值范围是（）

A、k>3 B、0<k<3 C、k<0 D、k<3

查看试题解析
9. 如图，在 $△ A B C$ 中， $A B = A C$ ， AD是角平分线，且 $A D = 8$ ， $B C = 12$ ，点E为 $A C$ 中点，则 $D E$ 的值为（）

A、5 B、5.8 C、6 D、6.5

查看试题解析
10. 勾股定理是我国的伟大数学发明之一.如图，以 $R t △ A B C$ 的各边为边向外作正方形，再把较小的两张正方形纸片放入最大的正方形中，三个阴影部分的面积分别为 $S_{1} = 1$ ， $S_{2} = 2$ ， $S_{3} = 3$ ，则较小两个正方形重叠部分（四边形 $D E F G$ ）的面积为（）

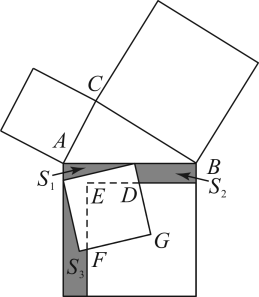A、4 B、5 C、5.5 D、6

查看试题解析

二、填空题

11. 在平面直角坐标系中，点A（－5，4）在第象限．

查看试题解析
12. 能说明命题：“若两个角 $α$ ， $β$ 互补，则这两个角必为一个锐角一个钝角”是假命题的反例是.

查看试题解析
13. 直线 $y = - 2 x + b$ 经过点 $(m ， y_{1})$ ， $(m - 4 ， y_{2})$ ，则 $y_{1}$ $y_{2}$ （填“ $<$ ”或“ $>$ ”）.

查看试题解析
14. 若关于x的不等式组 ${\begin{array}{l} 2 x - 5 < 0 \\ x - a > 0 \end{array}$ 有且仅有一个整数解 $x = 2$ ，则实数a的取值范围是.

查看试题解析
15. 已知 $△ A B C$ 是等腰直角三角形，且 $∠ C = 90 °$ ， $A C = B C = 2$ ，点D为AC的中点，动点E，F分别在AB，BC上运动，则 $△ D E F$ 周长的最小值为.

查看试题解析
16. 如图1，在平面直角坐标系中，四边形ABCD在第一象限内， $A D ∥ B C ∥ x$ 轴， $∠ A = 90 °$ ，直线 $y = 2 x + 4$ 沿x轴向其正方向平移，在平移过程中，直线被四边形 $A B C D$ 截得的线段长为t，直线向右平移的距离为m，图2是t与m之间的函数图象，则四边形 $A B C D$ 的面积为.

查看试题解析

三、解答题

17. 解不等式组 ${\begin{array}{l} 7 - 3 x \leq 1 \\ \frac{2 x - 1}{3} > \frac{x - 2}{2} \end{array}$ .

查看试题解析
18. 如图，在平面直角坐标系中， $A (- 4 ， 0)$ 、 $B (- 1 ， 0)$ 、 $C (- 6 ， 3)$ .

(1)、在图中作出 $△ A B C$ 关于y轴对称的图形 $△ A^{'} B^{'} C^{'}$ ；

(2)、写出 $A^{'}$ ， $C^{'}$ 的坐标；

(3)、求出 $△ A A^{'} C$ 的面积；

查看试题解析
19. 如图，一次函数 $y = k x + b$ 的图象经过点 $(- 2 ， 0)$ ， $(2 ， 2)$ .

(1)、求这个一次函数的表达式.

(2)、根据函数图象，直接写出 $y < 2$ 时x的取值范围.

查看试题解析
20. 如图， $∠ A = ∠ B$ ， $A E = B E$ ，点 $D$ 在 $A C$ 边上， $∠ C E D = ∠ A E B$ ， $A E$ 交 $B D$ 于点 $F$ .

(1)、求证： $△ A E C ≌ △ B E D$ ；

(2)、求证： $D E$ 平分 $∠ B D C$ .

查看试题解析
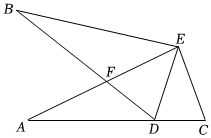21. 我校为了防控新型冠状病毒，购买了甲、乙两种消毒液进行校园环境消毒，已知学校第一次购买了甲种消毒液40瓶和乙种消毒液60瓶，共花费3600元；第二次购买了甲种消毒液30瓶和乙种消毒液20瓶，共花费1700元.

(1)、每瓶甲种消毒液和每瓶乙种消毒液的价格分别是多少元？

(2)、学校准备第三次购买这两种消毒液，其中乙种瓶数是甲种瓶数的2倍少4瓶，并且总花费不超过2920元，第三次最多能购买多少瓶甲种消毒液？

查看试题解析
22. A，B两地之间有一条长为600千米的公路，甲乙两车都从A地匀速开往B地，乙车先出发，然后甲车再出发，两车分别到达目的地后停止，已知甲乙两车相距的路程y（千米）与乙车行驶的时间x（时）之间的函数关系如图所示.

(1)、甲的速度为千米/时，乙的速度为千米/时.

(2)、求直线 $R S$ 的函数表达式.

(3)、当甲车与乙车相距的路程为80千米时，求此时乙车行驶的时间.

查看试题解析
23. 如图，在平面直角坐标系中，一次函数y=-x+1的图象分别与x轴、y轴交于点A，B，点C是x轴上一动点（不与点O，A重合），连结BC，作 $C D ⊥ B C$ ，且 $C D = B C$ ，过点D作 $D E ⊥ x$ 轴，垂足为点E.

(1)、求点A，B的坐标.

(2)、若点C在线段 $O A$ 上，连结 $D A$ ，猜想 $△ A E D$ 的形状，并证明结论.

(3)、若点C在x轴上，点D在x轴下方， $△ A C D$ 是以 $A C$ 为底边的等腰三角形，求点D的坐标.

查看试题解析
24. 如图，在锐角三角形 $A B C$ 中，点D，E分别在边 $A B$ ， $A C$ 上，连接 $D E$ ，将 $△ A D E$ 沿 $D E$ 翻折后，点A落在 $B C$ 边上的点P，当 $△ B D P$ 和 $△ C E P$ 均为等腰三角形时，我们把线段 $D E$ 称为 $△ A B C$ 的完美翻折线，P为完美点.

(1)、如图1，等边 $△ A B C$ 的边长为4，边 $B C$ 的中点P是完美点，写出完美翻折线 $D E$ 的长.

(2)、如图2，已知 $D E$ 为 $△ A B C$ 的完美翻折线，P为完美点.当 $∠ B$ ， $∠ C$ 都为等腰三角形顶角时，求此时 $∠ A$ 的度数.

(3)、已知在 $△ A B C$ 中， $A B = 6$ ， $A C = 5$ ，
①在（2）的条件下，求 $B C$ 的长.
②如图3， $D E$ 为 $△ A B C$ 的完美翻折线，P为完美点，当 $∠ B$ ， $∠ E P C$ 为顶角时，求 $\frac{B P}{C P}$ 的值.

查看试题解析