广东省河源市紫金县2022-2023学年七年级上学期期末考试数学试题
试卷更新日期:2023-03-01 类型:期末考试
一、选择题:本大题共10小题,每小题3分,共30分.
-
1. -2的倒数是( )A、 B、-2 C、 D、22. 2022年10月16日,中国共产党第二十次全国代表大会在北京人民大会堂开幕.开幕式中一组组亮眼的数据,展示了新时代十年发展的新成就.其中,国内生产总值从540000亿元增长到1140000亿元.把“1140000”用科学记数法表示为( )A、 B、 C、 D、3. 从左面观察如图所示的几何体,看到的几何体的形状图是( )
 A、
A、 B、
B、 C、
C、 D、
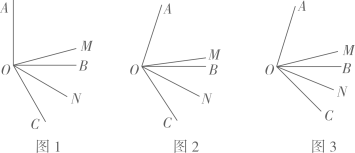
D、 4. 如图所示,某同学的家在处,他想尽快赶到附近处搭顺风车.他选择第②条路线,用几何知识解释其道理正确的是( )
4. 如图所示,某同学的家在处,他想尽快赶到附近处搭顺风车.他选择第②条路线,用几何知识解释其道理正确的是( ) A、两点确定一条直线 B、两点之间,线段最短 C、垂线段最短 D、经过一点有无数条直线5. 下列调查中,适合采用抽样调查的是( )A、疫情期间对全班学生的体温检测 B、学校招聘教师,对应聘人员进行面试 C、对八名同学的身高情况进行调查 D、对中学生目前的睡眠情况进行调查6. 下列各组中,属于同类项的是( )A、和 B、和 C、和 D、和7. 某文具店一支铅笔的售价为1.2元,一支圆珠笔的售价为2元.该店在“六·一”儿童节举行文具优惠售卖活动,铅笔按原价打八折出售,圆珠笔按原价打九折出售,结果两种笔共卖出60支,卖得金额87元.若设铅笔卖出支,则依题意可列得的一元一次方程为( )A、 B、 C、 D、8. 已知关于的方程是一元一次方程,则的值为( )A、1 B、-1 C、1或-1 D、以上结果均不正确9. 如图,一副三角板(直角顶点重合)摆放在桌面上,若 , 则( )
A、两点确定一条直线 B、两点之间,线段最短 C、垂线段最短 D、经过一点有无数条直线5. 下列调查中,适合采用抽样调查的是( )A、疫情期间对全班学生的体温检测 B、学校招聘教师,对应聘人员进行面试 C、对八名同学的身高情况进行调查 D、对中学生目前的睡眠情况进行调查6. 下列各组中,属于同类项的是( )A、和 B、和 C、和 D、和7. 某文具店一支铅笔的售价为1.2元,一支圆珠笔的售价为2元.该店在“六·一”儿童节举行文具优惠售卖活动,铅笔按原价打八折出售,圆珠笔按原价打九折出售,结果两种笔共卖出60支,卖得金额87元.若设铅笔卖出支,则依题意可列得的一元一次方程为( )A、 B、 C、 D、8. 已知关于的方程是一元一次方程,则的值为( )A、1 B、-1 C、1或-1 D、以上结果均不正确9. 如图,一副三角板(直角顶点重合)摆放在桌面上,若 , 则( ) A、30° B、45° C、50° D、60°10. 如图,用若干根小木棒拼成图形,拼第1个图形需要3根小木棒,拼第2个图形需要7根小小木棒,拼第3个图形需要11根小木棒……若按照这样的方法拼成第个图形需要103根小木棒,则的值为( )
A、30° B、45° C、50° D、60°10. 如图,用若干根小木棒拼成图形,拼第1个图形需要3根小木棒,拼第2个图形需要7根小小木棒,拼第3个图形需要11根小木棒……若按照这样的方法拼成第个图形需要103根小木棒,则的值为( ) A、34 B、36 C、26 D、24
A、34 B、36 C、26 D、24二、填空题:本大题共5小题,每小题3分,共15分.
-
11. 某正方体的每个面上都有一个汉字,如图是它的一种表面展开图,那么在原正方体中,与“功”字所在面相对面上的汉字是
 12. 用一个平面去截下列几何体:①圆柱; ②正方体; ③棱锥; ④圆锥; ⑤长方体; ⑥球, 其截出的面可能是圆的有 .(填序号)13.
12. 用一个平面去截下列几何体:①圆柱; ②正方体; ③棱锥; ④圆锥; ⑤长方体; ⑥球, 其截出的面可能是圆的有 .(填序号)13.如图,若CB=4cm,DB=7cm,且D是AC的中点,则AC=cm.
 14. 已知 , 则代数式的值为 .15. 在一条可以折叠的数轴上, , 表示的数分别是 , 4,如图,以点为折点,将此数轴向右对折,若点在点的右边,且 , 则点表示的数是 .
14. 已知 , 则代数式的值为 .15. 在一条可以折叠的数轴上, , 表示的数分别是 , 4,如图,以点为折点,将此数轴向右对折,若点在点的右边,且 , 则点表示的数是 .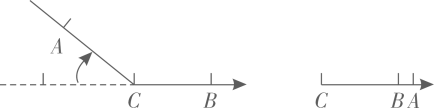
三、解答题(一):本大题共3小题,每小题8分,共24分.
-
16. 计算: .17. 一个几何体由一些大小相同的小立方块搭成,如图是从上面看到的这个几何体的形状图,小正方形上面的数字表示在该位置的小立方块的个数,请在网格中画出从正面和左面看到的该几何体的形状图.
 18. 解方程: =1.
18. 解方程: =1.四、解答题(二):本大题共3小题,每小题9分,共27分.
-
19. 随着科技的进步和网络资源的丰富,在线学习成为更多人的自主学习选择.某校计划为学生提供以下四类在线学习方式:在线阅读、在线听课、在线答题和在线讨论,为了解学生需求,该校随机对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调查(只能单选),并根据调查结果绘制成如下两幅不完整的统计图.
 (1)、本次共调查名学生;(2)、补全条形统计图;(3)、求扇形统计图中“在线讨论”对应的扇形圆心角的度数;(4)、该校共有学生3000名,请你估计该校对“在线阅读”最感兴趣的学生有多少名?20. 如图,已知线段 , , 是的中点.
(1)、本次共调查名学生;(2)、补全条形统计图;(3)、求扇形统计图中“在线讨论”对应的扇形圆心角的度数;(4)、该校共有学生3000名,请你估计该校对“在线阅读”最感兴趣的学生有多少名?20. 如图,已知线段 , , 是的中点. (1)、求线段的长;(2)、在上取一点 , 使得 , 求线段的长.21. 定义一种新运算:对任意有理数 , 都有 , 例如: .(1)、求的值;(2)、先化简,再求值: , 其中 , .
(1)、求线段的长;(2)、在上取一点 , 使得 , 求线段的长.21. 定义一种新运算:对任意有理数 , 都有 , 例如: .(1)、求的值;(2)、先化简,再求值: , 其中 , .五、解答题(三):本大题共2小题,每小题12分,共24分.