河北省定州市2022-2023学年高二上学期数学期末试卷

试卷更新日期：2023-02-28 类型：期末考试

进入出卷网下载

一、单选题

1. 抛物线 $y = 4 x^{2}$ 的焦点坐标为（）

A、 $(1 ， 0)$ B、 $(- 1 ， 0)$ C、 $(0 ， - \frac{1}{16})$ D、 $(0 ， \frac{1}{16})$

查看试题解析
2. “ $a = \pm 1$ ”是“直线 $x + y = 0$ 和直线 $x - a^{2} y = 0$ 垂直”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分又不必要条件

查看试题解析
3. 数列 ${a_{n}}$ 满足 $a_{n + 1} = 1 - \frac{1}{a_{n}} (n \in N^{*})$ ，且 $a_{1} = 2$ ，则 $a_{2022}$ 的值为（）

A、2 B、1 C、 $\frac{1}{2}$ D、-1

查看试题解析
4. 圆 ${(x + 2)}^{2} + {(y - 12)}^{2} = 4$ 关于直线 $x - y + 4 = 0$ 对称的圆的方程为（）

A、 ${(x + 6)}^{2} + {(y + 4)}^{2} = 4$ B、 ${(x + 8)}^{2} + {(y + 2)}^{2} = 4$ C、 ${(x - 8)}^{2} + {(y - 2)}^{2} = 4$ D、 ${(x - 6)}^{2} + {(y - 4)}^{2} = 4$

查看试题解析
5. 2022北京冬奥会开幕式将我国二十四节气融入倒计时，尽显中国人之浪漫．倒计时依次为：大寒、小寒、冬至、大雪、小雪、立冬、霜降、寒露、秋分、白露、处暑、立秋、大暑、小暑、夏至、芒种、小满、立夏、谷雨、清明、春分、惊蛰、雨水、立春，已知从冬至到夏至的日影长等量减少，若冬至、立冬、秋分三个节气的日影长之和为31.5寸，问大雪、寒露的日影长之和为（）

A、21寸 B、20.5寸 C、20寸 D、19.5寸

查看试题解析
6. 在以下命题中：
①三个非零向量 $\vec{a}$ ， $\vec{b}$ ， $\vec{c}$ 不能构成空间的一个基底，则 $\vec{a}$ ， $\vec{b}$ ， $\vec{c}$ 共面；
②若两个非零向量 $\vec{a}$ ， $\vec{b}$ 与任何一个向量都不能构成空间的一个基底，则 $\vec{a}$ ， $\vec{b}$ 共线；
③对空间任意一点 $O$ 和不共线的三点 $A$ ， $B$ ， $C$ ，若 $\vec{O P} = 2 \vec{O A} - \vec{2 O B} - \vec{2 O C}$ ，则 $P$ ， $A$ ， $B$ ， $C$ 四点共面
④若 $\vec{a}$ ， $\vec{b}$ 是两个不共线的向量，且 $\vec{c} = λ \vec{a} + μ \vec{b} (λ ， μ \in R ， λ ， μ \neq 0)$ ，则 ${\vec{a} ， \vec{b} ， \vec{c}}$ 构成空间的一个基底
⑤若 ${\vec{a} ， \vec{b} ， \vec{c}}$ 为空间的一个基底，则 ${\vec{a} + \vec{b} ， \vec{b} + \vec{c} + 2 \vec{a} ， \vec{c} + \vec{a}}$ 构成空间的另一个基底；其中真命题的个数是（）

A、0 B、1 C、2 D、3

查看试题解析
7. 足球起源于中国古代的蹴鞠游戏．“蹴”有用脚蹴、踢的含义，“鞠”最早系外包皮革、内饰米糠的球，因而“蹴鞠”就是指古人以脚蹴、踢皮球的活动，已知某“鞠”的表面上有四个点 $P ， A ， B ， C$ ，满足 $P A = 2$ ， $P A ⊥$ 面ABC， $A C$ ⊥ $B C$ ，若 $V_{P - A B C} = \frac{2}{3}$ ，则该“鞠”的体积的最小值为（）

A、 $\frac{4 \sqrt{2}}{3} π$ B、 $\frac{8 \sqrt{2}}{3} π$ C、 $\frac{9}{2} π$ D、 $\frac{9}{8} π$

查看试题解析
8. 如图， $F_{1}$ ， $F_{2}$ 分别是双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的左、右焦点，点 $P$ 是双曲线与圆 $x^{2} + y^{2} = a^{2} + b^{2}$ 在第二象限的一个交点，点 $Q$ 在双曲线上，且 $\vec{F_{1} P} = \frac{1}{2} \vec{F_{2} Q}$ ，则双曲线的离心率为（）

A、 $\frac{\sqrt{10}}{2}$ B、 $\sqrt{2}$ C、 $\sqrt{3}$ D、 $\frac{\sqrt{17}}{3}$

查看试题解析
9. 如果 $A B > 0$ ， $B C > 0$ ，那么直线 $A x + B y + C = 0$ 经过（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析

二、多选题

10. 等差数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ，若 $a_{1} > 0$ ，公差 $d \neq 0$ ，则（）

A、若 $S_{4} > S_{8}$ ，则 $S_{12} < 0$ B、若 $S_{4} = S_{8}$ ，则 $S_{6}$ 是 $S_{n}$ 中最大的项 C、若 $S_{5} > S_{6}$ ，则 $S_{4} > S_{5}$ D、若 $S_{3} > S_{4}$ ，则 $S_{4} > S_{5}$

查看试题解析
11. 如图，正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的棱长为1，则下列四个命题正确的是（）

A、两条异面直线 $D_{1} C$ 和 $B C_{1}$ 所成的角为 $\frac{π}{3}$ B、直线 $B C$ 与平面 $A B C_{1} D_{1}$ 所成的角等于 $\frac{π}{4}$ C、点D到面 $A C D_{1}$ 的距离为 $\sqrt{3}$ D、三棱柱 $A A_{1} D_{1} - B B_{1} C_{1}$ 外接球半径为 $\frac{\sqrt{3}}{2}$

查看试题解析
12. 1970年4月24日，我国发射了自己的第一颗人造地球卫星“东方红一号”，从此我国开始了人造卫星的新篇章，人造地球卫星绕地球运行遵循开普勒行星运动定律．卫星在以地球为焦点的椭圆轨道上绕地球运行时，其运行速度是变化的，速度的变化服从面积守恒规律，即卫星的向径（卫星与地球的连线）在相同的时间内扫过的面积相等．设椭圆的长轴长、焦距分别为 $2 a$ ， $2 c$ ，下列结论正确的（）

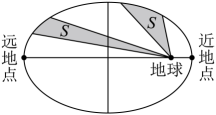A、卫星向径的取值范围是 $[a - c ， a + c]$ B、卫星在左半椭圆弧的运行时间大于其在右半椭圆弧的运行时间 C、卫星运行速度在近地点时最大，在远地点时最小 D、卫星向径的最小值与最大值的比值越小，椭圆轨道越圆

查看试题解析

三、填空题

13. 在三棱锥 $O - A B C$ 中， $O A ， O B ， O C$ 两两垂直， $O A = 3$ ， $O B = 4$ ， $O C = 5$ ， D是 $A B$ 的中点， $E$ 为 $O C$ 的中点，则 $D E$ 与平面 $O A B$ 所成的角的正切值为．

查看试题解析
14. 数列 ${a_{n}}$ 中，若 $a_{1} = 1$ ， $a_{n + 1} = \frac{n}{n + 2} a_{n}$ ，则 $a_{10} =$ ．

查看试题解析
15. 已知椭圆 $C ： \frac{x^{2}}{25} + \frac{y^{2}}{9} = 1$ 的左焦点为 $F$ ， $A ， B$ 是 $C$ 上关于原点对称的两点，且 $∠ A F B = 90 °$ ，则三角形 $A B F$ 的周长为．

查看试题解析
16. 已知函数 $f (x) = \sqrt{1 - {(x - 2)}^{2}} + 2$ 的图象上有且仅有两个不同的点关于直线 $y = 1$ 的对称点在 $y = - k x + 1$ 的图象上，则实数k的取值范围是．

查看试题解析

四、解答题

17. 已知等差数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ，且 $S_{8} = 100$ ， $a_{2} = 5$ ，设数列 ${b_{n}}$ 的前 $n$ 项和为 $P_{n} = 2^{n + 1} - 2$ ．

(1)、求数列 ${a_{n}}$ 和 ${b_{n}}$ 的通项公式；

(2)、设 $c_{n} = a_{n} b_{n}$ ，数列 ${c_{n}}$ 的前 $n$ 项和为 $T_{n}$ ．

查看试题解析
18. 已知 $△ A B C$ 的顶点 $B (3 ， 2)$ ， $A B$ 边上的高所在的直线方程为 $x - 2 y - 5 = 0$ ．

(1)、求直线 $A B$ 的方程；

(2)、在两个条件中任选一个，补充在下面问题中．
①角A的平分线所在直线方程为 $x + 2 y - 13 = 0$

②BC边上的中线所在的直线方程为 $2 x - y - 12 = 0$

_____，求直线 $A C$ 的方程．

查看试题解析
19. 已知圆 $C_{1} ： x^{2} + y^{2} = 10$ 与圆 $C_{2} ： x^{2} + y^{2} + 2 x + 2 y - 7 = 0$

(1)、求证：圆 $C_{1}$ 与圆 $C_{2}$ 相交；

(2)、求两圆公共弦所在直线的方程；

(3)、求经过两圆交点，且圆心在直线 $x + y - 6 = 0$ 上的圆的方程．

查看试题解析
20. 已知数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ， $a_{1} = 4$ ， $S_{n} - n = \frac{1}{2} (a_{n} + 2) ， (n \in N^{*})$ ．

(1)、求数列 ${a_{n}}$ 的通项公式 $a_{n}$ 和前 $n$ 项和 $S_{n}$ ；

(2)、设 $b_{k} = \frac{1}{(S_{2 k} + 2) S_{2 k + 1}} (k \in N^{*})$ ，数列 ${b_{n}}$ 的前 $n$ 项和记为 $T_{n}$ ，证明： $T_{n} < \frac{1}{8} ， (n \in N^{*})$

查看试题解析
21. 如图，直三棱柱 $A B C - A_{1} B_{1} C_{1}$ 的体积为4，点 $D$ ， $E$ 分别为 $A C$ ， $A A_{1}$ 的中点， $△ E C B$ 的面积为 $2 \sqrt{2}$ ．

(1)、求点A到平面 $E B C$ 的距离；

(2)、 $A A_{1} = 2 A B$ ，平面 $E B C ⊥$ 平面 $A B B_{1} A_{1}$ ，求平面 $D B E$ 与平面 $B E C_{1}$ 所成角的余弦值．

查看试题解析
22. 在一张纸上有一圆 $C ： {(x + \sqrt{3})}^{2} + y^{2} = 8$ ，定点 $M (\sqrt{3} ， 0)$ ，折叠纸片使圆C上某一点 $M_{1}$ 恰好与点M重合，这样每次折叠都会留下一条直线折痕EF，设折痕EF与直线 $M_{1} C$ 的交点为T．

(1)、求证： $| | T C | - | T M | |$ 为定值，并求出点 $T$ 的轨迹 $C^{'}$ 方程；

(2)、已知点 $A (2 ， 1)$ ，直线l交 $C^{'}$ 于P，Q两点，直线AP、AQ的斜率之和为0．若 $t a n ∠ P A Q = 2 \sqrt{2}$ ，求 $△ P A Q$ 的面积．

查看试题解析