广东省广州市2022-2023学年高二上学期数学期末试卷
试卷更新日期:2023-02-28 类型:期末考试
一、单选题
-
1. 直线的倾斜角为( )A、 B、 C、 D、2. 已知圆的方程为 , 则圆心的坐标为( )A、 B、 C、 D、3. 已知双曲线 , 则该双曲线的离心率为( )A、 B、 C、 D、4. 等差数列 中,已知 , ,则公差d等于( )A、3 B、-6 C、4 D、-35. 已知点到直线的距离为1,则的值为( )A、-5或-15 B、-5或15 C、5或-15 D、5或156. 已知等比数列的各项均为正数,公比 , 且满足 , 则( )A、8 B、4 C、2 D、17. 如图所示,在平行六面体中,E,F,H分别为 , , DE的中点.若 , , , 则向量可用表示为( )
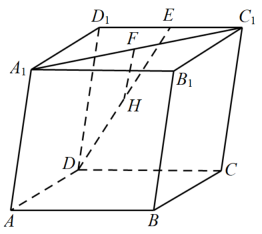 A、 B、 C、 D、8. 已知椭圆的右焦点与抛物线的焦点重合,过点的直线交于两点,若的中点坐标为 , 则椭圆方程为( )A、 B、 C、 D、
A、 B、 C、 D、8. 已知椭圆的右焦点与抛物线的焦点重合,过点的直线交于两点,若的中点坐标为 , 则椭圆方程为( )A、 B、 C、 D、二、多选题
-
9. 已知非零空间向量 , 则下列说法正确的是( )A、若 , 则 B、 C、 D、若 , 则不共面10. 已知点在圆:上,直线 , 则( )A、直线与圆相交 B、直线与圆相离 C、点到直线距离最大值为 D、点到直线距离最小值为11. 设为等比数列的前n项和,已知 , , 则下列结论正确的是( )A、 B、 C、 D、12. 已知椭圆的中心为坐标原点,焦点在轴上,短轴长等于2,离心率为 , 过焦作轴的垂线交椭圆于两点,则下列说法正确的是( )A、椭圆的方程为 B、椭圆的方程为 C、 D、
三、填空题
-
13. 已知 , , 则向量的坐标为.14. 古希腊著名科学家毕达哥拉斯把1,3,6,10,15,21,…这些数量的(石子),排成一个个如图一样的等边三角形,从第二行起每一行都比前一行多1个石子,像这样的数称为三角形数.那么把三角形数从小到大排列,第11个三角形数是.
 15. 已知抛物线 , 直线过抛物线的焦点,直线与抛物线交于两点,弦长为12,则直线的方程为.16. 数学著作《圆锥曲线论》中给出了圆的一种定义:平面内,到两个定点A,B距离之比是常数( , )的点M的轨迹是圆.若两定点 , , 动点M满足 , 点M的轨迹围成区域的面积为 , △ABM面积的最大值为.
15. 已知抛物线 , 直线过抛物线的焦点,直线与抛物线交于两点,弦长为12,则直线的方程为.16. 数学著作《圆锥曲线论》中给出了圆的一种定义:平面内,到两个定点A,B距离之比是常数( , )的点M的轨迹是圆.若两定点 , , 动点M满足 , 点M的轨迹围成区域的面积为 , △ABM面积的最大值为.四、解答题
-
17. 已知圆的圆心为 , 且经过点.(1)、求圆的标准方程;(2)、已知直线与圆相交于两点,求.18. 已知数列的前n项和为 , 且(1)、求的通项公式(2)、求证数列是等差数列19. 如图,在棱长为2的正方体中,分别为的中点.
 (1)、求证:;(2)、求点到平面的距离.
(1)、求证:;(2)、求点到平面的距离.
