云南省昭通市永善县2021-2022学年八年级下学期期中数学试题

试卷更新日期：2023-02-28 类型：期中考试

进入出卷网下载

一、单选题

1. 下列二次根式中，属于最简二次根式的是（）

A、 $\sqrt{0.8}$ B、 $\sqrt{6}$ C、 $\sqrt{4}$ D、 $\sqrt{\frac{1}{2}}$

查看试题解析
2. 若平行四边形中两个内角的度数比为 $1 ： 3$ ，则其中较大的内角是（）

A、 $45 °$ B、 $75 °$ C、 $105 °$ D、 $135 °$

查看试题解析
3. 如图，阴影部分是一个长方形，它的面积是（）

A、 $48 c m^{2}$ B、 $20 c m^{2}$ C、 $14 c m^{2}$ D、 $10 c m^{2}$

查看试题解析
4. 在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $B C = 2$ ， $A C = 1$ ，点B、C在数轴上，以点B为圆心， $A B$ 长为半径画弧，交数轴于点D，则D点表示的数是（）

A、 $3 - \sqrt{3}$ B、 $3 - \sqrt{5}$ C、 $3 - \sqrt{3}$ 或 $3 + \sqrt{3}$ D、 $3 - \sqrt{5}$ 或 $3 + \sqrt{5}$

查看试题解析
5. 下列运算正确的是（）

A、 $a^{3} \cdot a^{2} = a^{6}$ B、 $| - 5 | = 5$ C、 ${(\frac{1}{2})}^{- 1} = - 2$ D、 $\sqrt{9} = \pm 3$

查看试题解析
6. 若代数式 $\frac{x}{\sqrt{x - 1}}$ 在实数范围内有意义，则x的取值范围是（）

A、 $x \neq 1$ B、 $x ≥ 1$ C、 $x > 1$ D、 $x > 1$ 且 $x \neq 0$

查看试题解析
7. 如图，四边形 $A B C D$ 是正方形，延长 $A B$ 到点 $E$ ，使 $A E = A C$ ，则 $∠ B C E$ 的度数是（）

A、 $62.5 °$ B、 $45 °$ C、 $32.5 °$ D、 $22.5 °$

查看试题解析
8. 如图，在四边形 $A B C D$ 中，E、F、G、H分别是 $A B$ 、 $B D$ 、 $C D$ 、 $A C$ 的中点，要使四边形 $E F G H$ 是菱形，四边形 $A B C D$ 还应满足的一个条件是（）

A、 $A C = B D$ B、 $A C ⊥ B D$ C、 $A D = B C$ D、 $A B = D C$

查看试题解析
9. 如图四边形ABCD是菱形，对角线AC＝8，BD＝6，DH⊥AB于点H，则DH的长度是（　　）

A、 $\frac{12}{5}$ B、 $\frac{16}{5}$ C、 $\frac{24}{5}$ D、 $\frac{48}{5}$

查看试题解析
10. 下列命题中，正确的个数是（）
①若三条线段的比为 $1 ： 1 ： \sqrt{2}$ ，则它们可以组成一个等腰直角三角形；
②对角线相等的平行四边形是矩形；
③对角线互相垂直的四边形是菱形；
④各边都相等的多边形是正多边形；
⑤对角线互相垂直平分的四边形是正方形．

A、2个 B、3个 C、4个 D、5个

查看试题解析
11. 如图所示，菱形 $A B C D$ 中，对角线 $A C$ ， $B D$ 相交于点O，H为 $A D$ 边中点，菱形 $A B C D$ 的周长为24，则 $O H$ 的长等于（）

A、6 B、5 C、4 D、3

查看试题解析
12. 如图，在正方形 $A B C D$ 中，P是边 $A B$ 上一动点（不与A、B重合），对角线 $A C$ 、 $B D$ 相交于点O，过点P分别作 $A C$ 、 $B D$ 的垂线，分别交 $A C$ 、 $B D$ 于点E、F，交 $A D$ 、 $B C$ 于点M、N，下列结论：
① $△ A P E ≅ △ A M E$ ；
② $P M + P N = A C$ ；
③ $P E^{2} + P F^{2} = P O^{2}$ ；
④当P是 $A B$ 的中点时， $S_{△ A P M} = \frac{2}{3} S_{△ P M N}$ ．
其中正确的结论有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

13. $(\sqrt{3} - 2) (\sqrt{3} + 2) =$ ．

查看试题解析
14. 已知菱形的两条对角线长分别为3和4，则菱形的面积为．

查看试题解析
15. 若 $| 1 - m | + \sqrt{n^{2} - 6 n + 9} = 0$ ，则 $\sqrt{m + n} =$ ．

查看试题解析
16. 小华想知道学校旗杆的高，他发现旗杆上的绳子垂到地面还多 $1 m$ ，当它把绳子的下端拉开 $\sqrt{37} m$ 后，发现下端刚好触到地面，则旗杆的高为 $m$ ．

查看试题解析
17. 如图，把矩形 $A B C D$ 沿 $E F$ 翻折，点B恰好落在 $A D$ 边的 $B'$ 处，若 $A E = 2$ ， $D E = 6$ ， $∠ E F B = 6 0^{∘}$ ，则矩形 $A B C D$ 的面积是．

查看试题解析
18. 将n个边长都为1的正方形按如图所示的方法摆放，点 $A_{1}$ ， $A_{2}$ ， …， $A_{n}$ 分别是正方形对角线的交点，则2022个正方形照这样重叠形成的重叠部分的面积和为．

查看试题解析

三、解答题

19. 计算：

(1)、 $\sqrt{8} + \sqrt{32} - \sqrt[3]{27}$

(2)、 $(π - \sqrt{5})^{0} + | 2 - \sqrt{2} | - {(\frac{1}{3})}^{- 1} + \sqrt{8}$

查看试题解析
20. 甲、乙两船从港口B同时出发，甲船向北偏东 $56 °$ 的方向航行，乙船以16海里/时的速度向南偏东 $34 °$ 的方向航行，3小时后，甲船到达M岛，乙船到达P岛，若M、P两岛相距60海里，请求出甲船的航速是多少？

查看试题解析
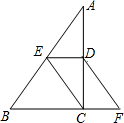
21. 如图在△ABC中， $∠$ ACB=90°，点D，E分别是AC、AB的中点，点F在BC的延长线上，且 $∠$ CDF= $∠$ A．
求证：四边形DECF是平行四边形.

查看试题解析
22. 如图，矩形 $A B C D$ 的对角线 $A C$ 、 $B D$ 相交于点O， $D E ∥ A C$ ， $O D ∥ C E$ ．

(1)、求证：四边形 $O C E D$ 为菱形；

(2)、若 $A F$ 垂直平分线段 $B O$ 于点F， $A C = 10$ ，求 $A D$ 的长．

查看试题解析
23. 如图，在等边三角形 $A B C$ 中， $B C = 9 c m$ ，射线 $A G ∥ B C$ ，点E从点A出发沿射线 $A G$ 以 $1 m / s$ 的速度运动；同时点F从点B出发沿射线 $B C$ 以 $2 c m / s$ 的速度运动．连接 $E F$ ，设运动时间为 $t (s)$ ．

(1)、试求当t为何值时， $A C$ 与 $E F$ 互相平分；

(2)、试求当t为何值时，四边形 $A C F E$ 是菱形．

查看试题解析
24. 如图， $△ A B C$ 中，点O是 $A C$ 边上的一点，过点O作直线 $M N ∥ B C$ ，分别交 $∠ A C D$ 、 $∠ A C B$ 的平分线于点F、E，连接 $A E$ 、 $A F$ ，且点B、C、D在同一直线上．

(1)、求证： $O E = O F$ ；

(2)、当点O为 $A C$ 中点时，四边形 $A E C F$ 是什么特殊四边形，并说明理由；

(3)、在（2）的条件下，当 $△ A B C$ 满足什么条件时，四边形 $A E C F$ 为正方形，并加以证明．

查看试题解析