辽宁省铁岭市铁岭县2021-2022学年八年级下学期期中数学试题

试卷更新日期：2023-02-28 类型：期中考试

进入出卷网下载

一、单选题

1. 下列式子中一定是二次根式的是（）

A、 $\sqrt{- a}$ B、 $\sqrt{a^{2}}$ C、 $\sqrt{- a^{2}}$ D、 $\sqrt{a^{3}}$

查看试题解析
2. 用一根 $10 c m$ 长的铁丝围成的矩形，现给出四个量：①长方形的长；②长方形的宽；③长方形的周长；④长方形的面积．其中是变量的有（）

A、1个 B、2个 C、3个 D、4.

查看试题解析
3. 下列各组数可以构成直角三角形的是（）

A、3，5，6 B、2，3，4 C、6，7，9 D、3，4，5

查看试题解析
4. 下列二次根式中属于最简二次根式的是（　　）

A、 $\sqrt{14}$ B、 $\sqrt{48}$ C、 $\sqrt{\frac{a}{b}}$ D、 $\sqrt{4 a + 4}$

查看试题解析
5. 下列性质中，菱形具有而矩形不一定具有的是（）

A、对角相等 B、对边相等 C、对角线互相平分 D、对角线互相垂直

查看试题解析
6. 小张的爷爷每天坚持锻炼，星期天爷爷从家里跑步到公园，打了一会太极拳，然后沿原路漫步走到家，下面能反映当天爷爷离家的距离y米与时间t分钟之间关系的大致图象是（）

A、 B、 C、 D、

查看试题解析
7. 如图，在▱ABCD中，对角线AC的垂直平分线分别交AD，BC于点E，F，连接CE，若△CED的周长为6，则▱ABCD的周长为（）

A、6 B、12 C、18 D、24

查看试题解析
8. 计算 $\sqrt{\frac{b}{a}} \div \sqrt{a b} \times \sqrt{\frac{1}{a b}} (a > 0 ， b > 0)$ 等于（）

A、 $\frac{1}{a^{2} b} \sqrt{a b}$ B、 $\frac{1}{a b^{2}} \sqrt{a b}$ C、 $\frac{1}{b} \sqrt{a b}$ D、 $b \sqrt{a b}$

查看试题解析
9. 小明在学习了正方形之后，给同桌小文出了道题，从下列四个条件：①AB=BC，②∠ABC=90°，③AC=BD，④AC⊥BD中选两个作为补充条件，使▱ABCD为正方形（如图），现有下列四种选法，你认为其中错误的是（）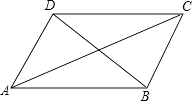

A、①② B、②③ C、①③ D、②④

查看试题解析
10. 如图，在矩形ABCD中， $A B = 4 ， B C = 6$ ，点E为BC的中点，将 $△ A B E$ 沿AE折叠，使点B落在矩形内点F处，连接CF.则CF的长为（）

A、 $\frac{18}{5}$ B、 $\frac{16}{5}$ C、 $\frac{12}{5}$ D、 $\frac{9}{5}$

查看试题解析

二、填空题

11. 函数y= $\sqrt{x - 1}$ 的自变量x的取值范围是．

查看试题解析
12. 化简： $\sqrt{18} - \sqrt{8} + \sqrt{12} - \sqrt{3} =$ ．

查看试题解析
13. 如图，在平行四边形ABCD中， $A B = 6 ， B C = 8 ， ∠ B C D$ 的平分线交AD于点E，交BA的延长线于点F，则 $A E + A F$ 的值为．

查看试题解析
14. 等腰三角形的两条中位线分别为3和5，则等腰三角形的周长为．

查看试题解析
15. 已知函数 $y = 2 x + 1$ 中当 $x = 1$ 时，则函数值y= ．

查看试题解析
16. 菱形ABCD的对角线 $A C ， B D$ 相交于点O，E为AD的中点，若 $O E = 2$ ，则菱形ABCD的周长＝．

查看试题解析
17. 如图，一名考生步行前往考场，10分钟走了总路程的 $\frac{1}{4}$ ，估计步行不能准时到达，于是他也改乘出租车赶往考场，他行驶的路程 $s (k m)$ 与时间 $t (m i n)$ 之间关系如图（假定总路程为1），则他实际到达考场所在的时间比一直步行提前了分钟．

查看试题解析
18. 如图，点E是正方形ABCD的边CD上一点，延长CB到点F，使 $B F = D E$ ，连接 $A E ， A F ， E F$ ，作 $A H ⊥ E F$ 交BC于点G，垂足为点H，连接CH．有下列四个结论：① $△ A B F ≌ △ A D E$ ；② $∠ E A G = 45 °$ ；③ $∠ C F E = 25 °$ ；④ $C H = H F$ ．其中正确的结论有（填写序号）

查看试题解析

三、解答题

19. 计算：

(1)、 $\sqrt{27} - \sqrt{12} + \frac{1}{4} \sqrt{48}$

(2)、 $\sqrt{3} (1 - \sqrt{3}) + \sqrt{12} + {(\frac{1}{3})}^{- 1}$

(3)、 $2 \sqrt{12} \times \frac{\sqrt{3}}{4} \div 3 \sqrt{2}$

(4)、 $(3 \sqrt{2} + \sqrt{7}) (3 \sqrt{2} - \sqrt{7})$

查看试题解析
20. 在如图所示的平面直角坐标系中，按要求解决下列问题：

(1)、描出点 $A (- 2 ， - 2) ， B (- 8 ， 6) ， C (2 ， 1)$

(2)、连接 $A B ， B C ， A C$ ，判断 $△ A B C$ 的形状，并说明理由；

(3)、 $△ A B C$ 的面积为

查看试题解析
21. 已知 $x = \sqrt{3} + \sqrt{2} ， y = \sqrt{3} - \sqrt{2}$ ，求x³y+xy³的值．

查看试题解析
22. 如图，在四边形ABCD中， $∠ A = ∠ C = 90 ° ， A B = 2 ， C D = 6 ， ∠ D = 45 °$ ．求：四边形ABCD的面积．

查看试题解析
23. 如图．点B，E，C，F在同一条直线上， $A B ∥ D E ， A C ∥ D F ， B E = C F$ ，连接AD．求证：

(1)、 $△ A B C ≌ △ D E F$ ：

(2)、四边形ABED是平行四边形．

查看试题解析
24. 如图，菱形ABCD的对角线相交于点O，分别过点C，D作 $C E ∥ B D ， D E ∥ A C$ 且两平行线相交于点E．

(1)、求证：四边形OCED是矩形；

(2)、若 $C E = 1 ， D E = 2$ ，求菱形ABCD的面积．

查看试题解析
25. 如图，点E为正方形ABCD内一点， $∠ A E B = 90 °$ ，过点B作 $B G ⊥ B E$ 且使 $B G = B E$ ，连接CG交AE的延长线于点F．

(1)、填空： $△ A B E$ $△ C B G$ （填“全等”或“不全等”）；

(2)、判断四边形BGFE的形状，并说明理由；

(3)、若 $D A = D E$ ，请猜想线段CF与FG的数量关系，并加以证明．

查看试题解析