辽宁省铁岭市2021-2022学年八年级下学期期中数学试题
试卷更新日期:2023-02-28 类型:期中考试
一、单选题
-
1. 下列是不等式的是( )A、 B、 C、 D、2. 下列图形中,是中心对称图形的是( )A、等边三角形 B、正五边形 C、平行四边形 D、等腰直角三角形3. 若 ,则下列各式正确的是( )A、 B、 C、 D、4. 如图,在 中, 是AC上一点, 于点E, 连接BD,若AC=8cm,则 等于( )
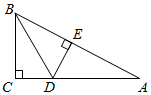 A、6cm B、7cm C、8cm D、9cm5. 如果关于x的不等式 (a+1) x>a+1的解集为x<1,那么a的取值范围是( )A、a>0 B、a<0 C、a>-1 D、a<-16.
A、6cm B、7cm C、8cm D、9cm5. 如果关于x的不等式 (a+1) x>a+1的解集为x<1,那么a的取值范围是( )A、a>0 B、a<0 C、a>-1 D、a<-16.已知,如图,在△ABC中,OB和OC分别平分∠ABC和∠ACB,过O作DE∥BC,分别交AB、AC于点D、E,若BD+CE=5,则线段DE的长为( )
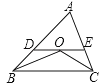 A、5 B、6 C、7 D、87. 如图,一次函数与的图像相交于点 , 则关于x的不等式的解集是( )
A、5 B、6 C、7 D、87. 如图,一次函数与的图像相交于点 , 则关于x的不等式的解集是( )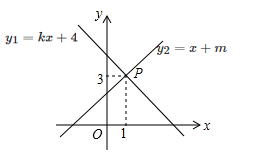 A、 B、 C、 D、8. 若不等式组 的解集是x<2,则a的取值范围是( )A、a<2 B、a≤2 C、a≥2 D、无法确定9. 把不等式组的解表示在数轴上,正确的是( )A、
A、 B、 C、 D、8. 若不等式组 的解集是x<2,则a的取值范围是( )A、a<2 B、a≤2 C、a≥2 D、无法确定9. 把不等式组的解表示在数轴上,正确的是( )A、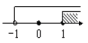 B、
B、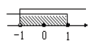 C、
C、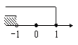 D、
D、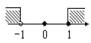 10. 如图:等边三角形ABC中,BD=CE,AD与BE相交于点P,则∠APE的度数是( )
10. 如图:等边三角形ABC中,BD=CE,AD与BE相交于点P,则∠APE的度数是( )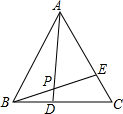 A、45° B、55° C、60° D、75°
A、45° B、55° C、60° D、75°二、填空题
-
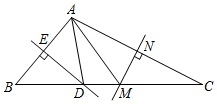
11. 用不等式表示:x与5的差不大于x的2倍: .12. 若一次函数的图象经过点 , 则不等式的解集为 .13. 如图,DE,MN分别垂直平分AB,AC,且 cm,则 的周长为cm.
 14. 如图,在 中, 是 的角平分线 ,垂足为E,若CD=6,则 .
14. 如图,在 中, 是 的角平分线 ,垂足为E,若CD=6,则 .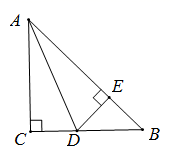 15. 不等式组 的解集是x>4,那么m的取值范围是 .16. 若关于 的不等式 只有3个正整数解,则 的取值范围是.17. 如图,已知△ABC中,∠ABC=45°,AC=4,H是高AD和BE的交点,则线段BH的长度为 .
15. 不等式组 的解集是x>4,那么m的取值范围是 .16. 若关于 的不等式 只有3个正整数解,则 的取值范围是.17. 如图,已知△ABC中,∠ABC=45°,AC=4,H是高AD和BE的交点,则线段BH的长度为 .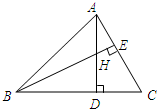 18. 如图,在 中, ,点M,N分别是AB,AC上的动点,沿MN所在的直线折叠,使点A的对应点 始终落在BC上, 若为直角三角形,则BM的长为;
18. 如图,在 中, ,点M,N分别是AB,AC上的动点,沿MN所在的直线折叠,使点A的对应点 始终落在BC上, 若为直角三角形,则BM的长为;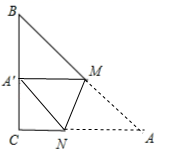
三、解答题
-
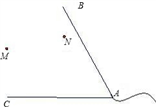
19. 某开发区在两条河BA与CA所夹的角之间,M、N是两个工厂,现要在开发区内建一个货物中转站,要求它到两条河的距离相等,到两工厂的距离也相等,请找出货物中转站的位置P.(用尺规作图,不写作法,保留痕迹)
 20. 解下列不等式:(1)、(2)、21. 如图,在△ABC中,AB=AC,点D,E,F分别在AB,BC,AC上,且BD=CE, BE=CF.
20. 解下列不等式:(1)、(2)、21. 如图,在△ABC中,AB=AC,点D,E,F分别在AB,BC,AC上,且BD=CE, BE=CF.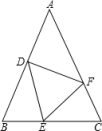 (1)、求证:△DEF是等腰三角形.(2)、当∠A=60°,DE=6,求△DEF的周长.22. 如图,在△ABC中,∠ABC的平分线与∠ACB的外角的平分线相交于点P,连接AP.
(1)、求证:△DEF是等腰三角形.(2)、当∠A=60°,DE=6,求△DEF的周长.22. 如图,在△ABC中,∠ABC的平分线与∠ACB的外角的平分线相交于点P,连接AP.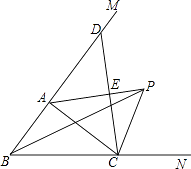 (1)、求证:PA平分∠BAC的外角∠CAM;(2)、过点C作CE⊥AP,E是垂足,并延长CE交BM于点D.求证:CE=ED.23. 某单位要印刷一批宣传材料。在甲印刷厂不管一次印刷多少页,每页收费0.1元,在乙印刷厂,一次印刷页数不超过20时,每页收费0.12元,一次印刷页数超过20时,超过部分每页收费0.09元,设该单位需要印刷宣传材料的页数为x(x>20且x是整数),在甲印刷厂实际付费为 (元),在乙印刷厂实际收费为 (元)(1)、分别写出 与x的函数关系式;(2)、你认为选择哪家印刷厂印刷这些宣传材料较好?为什么?24. 某中学计划为地理兴趣小组购买大、小两种地球仪,若购买1个大地球仪和3个小地球仪需用136元;若购买2个大地球仪和1个小地球仪需用132元.(1)、求每个大地球仪和每个小地球仪各多少钱?(2)、该中学决定购买以上两种地球仪共30个,总费用不超过980元,那么至少要购买多少个小地球仪?25. 如图,在△ABC中,∠BAC=90°,AB=AC,AD⊥BC于点D.
(1)、求证:PA平分∠BAC的外角∠CAM;(2)、过点C作CE⊥AP,E是垂足,并延长CE交BM于点D.求证:CE=ED.23. 某单位要印刷一批宣传材料。在甲印刷厂不管一次印刷多少页,每页收费0.1元,在乙印刷厂,一次印刷页数不超过20时,每页收费0.12元,一次印刷页数超过20时,超过部分每页收费0.09元,设该单位需要印刷宣传材料的页数为x(x>20且x是整数),在甲印刷厂实际付费为 (元),在乙印刷厂实际收费为 (元)(1)、分别写出 与x的函数关系式;(2)、你认为选择哪家印刷厂印刷这些宣传材料较好?为什么?24. 某中学计划为地理兴趣小组购买大、小两种地球仪,若购买1个大地球仪和3个小地球仪需用136元;若购买2个大地球仪和1个小地球仪需用132元.(1)、求每个大地球仪和每个小地球仪各多少钱?(2)、该中学决定购买以上两种地球仪共30个,总费用不超过980元,那么至少要购买多少个小地球仪?25. 如图,在△ABC中,∠BAC=90°,AB=AC,AD⊥BC于点D.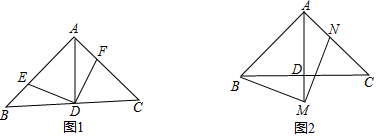 (1)、如图1,点E,F在AB,AC上,且∠EDF=90°.求证:BE=AF;(2)、点M,N分别在直线AD,AC上,且∠BMN=90°.如图2,当点M在AD的延长线上时,求证:AB+AN= AM;26. 如图,是的平分线,点E,M分别在射线上,作射线 , 以M为中心,将射线逆时针旋转 , 交所在直线于点F.
(1)、如图1,点E,F在AB,AC上,且∠EDF=90°.求证:BE=AF;(2)、点M,N分别在直线AD,AC上,且∠BMN=90°.如图2,当点M在AD的延长线上时,求证:AB+AN= AM;26. 如图,是的平分线,点E,M分别在射线上,作射线 , 以M为中心,将射线逆时针旋转 , 交所在直线于点F.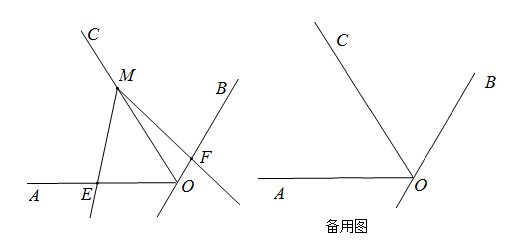 (1)、按要求画图,并完成证明.
(1)、按要求画图,并完成证明.过点M作 , 交射线于点H,求证:是等边三角形.
(2)、当点F落在射线上,请猜想线段三者之间的数量关系,并说明理由;(3)、当点F落在射线的反向延长线上,请直接写出线段三者之间的数量关系.