辽宁省沈阳市沈北新区2021-2022学年八年级下学期期中数学试题
试卷更新日期:2023-02-28 类型:期中考试
一、单选题
-
1. 拼图游戏需要将形状各异的组件拼在一起,下列拼图组件是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 数x不大于3是指( )A、 B、 C、 D、3. 若 ,则下列结论错误的是( )A、 B、 C、 D、4. 如图,直线m∥n,点A在直线m上,点B、C在直线n上,AB=CB,∠1=70°,则∠BAC等于( )
2. 数x不大于3是指( )A、 B、 C、 D、3. 若 ,则下列结论错误的是( )A、 B、 C、 D、4. 如图,直线m∥n,点A在直线m上,点B、C在直线n上,AB=CB,∠1=70°,则∠BAC等于( )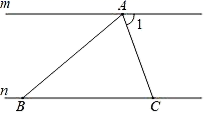 A、40° B、55° C、70° D、110°5. 如图,将△AOB绕点O按逆时针方向旋转45°后得到△A'OB',若∠AOB=15°,则∠AOB'的度数是( ).
A、40° B、55° C、70° D、110°5. 如图,将△AOB绕点O按逆时针方向旋转45°后得到△A'OB',若∠AOB=15°,则∠AOB'的度数是( ). A、25° B、30° C、35° D、40°6. 不等式5+2x <1的解集在数轴上表示正确的是( ).A、
A、25° B、30° C、35° D、40°6. 不等式5+2x <1的解集在数轴上表示正确的是( ).A、 B、
B、 C、
C、 D、
D、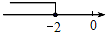 7. 如图,于点D,于点F, . 要根据“”证明 , 则还需要添加的条件是( )
7. 如图,于点D,于点F, . 要根据“”证明 , 则还需要添加的条件是( )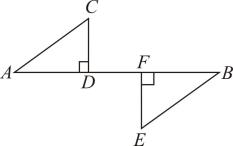 A、 B、 C、 D、8. 如图,一次函数的图像经过、两点,则不等式的解集是( )
A、 B、 C、 D、8. 如图,一次函数的图像经过、两点,则不等式的解集是( )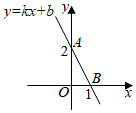 A、 B、 C、 D、9. 某种商品的进价为800元,出售时标价为1200元,后来由于该商品积压,商店准备打折销售,但要保证利润率不低于5%,则至多可打( )A、6折 B、7折 C、8折 D、9折10. 如图,在△ABC中,AB=AC,∠A=30°,AC的垂直平分线分别交AB,AC于D,E.连接CD,若CD=1cm,则BD的长为( )
A、 B、 C、 D、9. 某种商品的进价为800元,出售时标价为1200元,后来由于该商品积压,商店准备打折销售,但要保证利润率不低于5%,则至多可打( )A、6折 B、7折 C、8折 D、9折10. 如图,在△ABC中,AB=AC,∠A=30°,AC的垂直平分线分别交AB,AC于D,E.连接CD,若CD=1cm,则BD的长为( )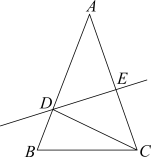 A、1cm B、(-1)cm C、cm D、cm
A、1cm B、(-1)cm C、cm D、cm二、填空题
-
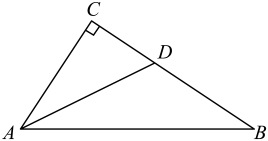
11. 不等式2x﹣1≤6的非负整数解有个.12. 如图,在△ABC中,∠C=90°,AD平分∠CAB,CD=2,则D点到AB的距离是 .
 13. 在平面直角坐标系中,将点(﹣2,4)向下平移3个单位长度,则所得的点的坐标为 .14. 用反证法证明某一命题的结论“ ”时,应假设.15. 已知等腰三角形一腰上的高线长等于腰长的一半,则这个等腰三角形的顶角的度数为16. 如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ.以下五个结论:①;②PQ//AE;③;④△CPQ为等边三角形;⑤;其中正确的有(注:把你认为正确的答案序号都写上)
13. 在平面直角坐标系中,将点(﹣2,4)向下平移3个单位长度,则所得的点的坐标为 .14. 用反证法证明某一命题的结论“ ”时,应假设.15. 已知等腰三角形一腰上的高线长等于腰长的一半,则这个等腰三角形的顶角的度数为16. 如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ.以下五个结论:①;②PQ//AE;③;④△CPQ为等边三角形;⑤;其中正确的有(注:把你认为正确的答案序号都写上)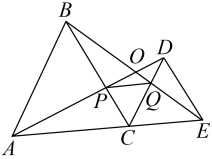
三、解答题
-
17. 解不等式: .18. 解不等式组 , 请按下列步骤完成解答:
解:
(1)、解不等式①,得:;(2)、解不等式②,得:;(3)、把不等式①和②的解集在如下的数轴上表示出来: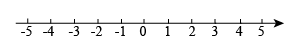 (4)、原不等式组的解集是 .19. 解不等式组:20. 如图,在△ABC中,∠CAB=70°,将△ABC绕点A逆时针旋转到△A的位置,使得 .
(4)、原不等式组的解集是 .19. 解不等式组:20. 如图,在△ABC中,∠CAB=70°,将△ABC绕点A逆时针旋转到△A的位置,使得 .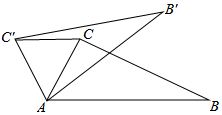 (1)、请判断△ACC'的形状,并说明理由.(2)、求∠BAB'的度数.21. 如图,正方形网格中,每个小方格都是边长为1的正方形△ABC的三个顶点都在格点上,结合所给的平面直角坐标系解答下列问题:
(1)、请判断△ACC'的形状,并说明理由.(2)、求∠BAB'的度数.21. 如图,正方形网格中,每个小方格都是边长为1的正方形△ABC的三个顶点都在格点上,结合所给的平面直角坐标系解答下列问题: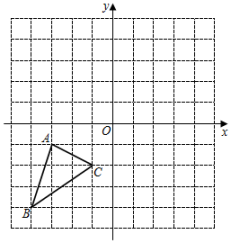
( 1 )将△ABC向上平移5个单位长度,画出平移后的△A1B1C1;
( 2 )将△A1B1C1绕坐标原点O顺时针方向旋转90°,出旋转后的△A2B2C2 .
22. 小明要代表班级参加学校举办的消防知识竞赛,共有25道题,规定答对一道题得6分,答错或不答一道题扣2分,只有得分超过90分才能获得奖品,问小明至少答对多少道题才能获得奖品?23. 已知:如图一次函数y1=﹣x﹣2与y2=x﹣4的图象相交于点A. (1)、求点A的坐标;(2)、若一次函数y1=﹣x﹣2与y2=x﹣4的图象与x轴分别相交于点B、C,求△ABC的面积.(3)、结合图象,直接写出y1≥y2时x的取值范围.24. 如图,在△ABC中,∠ACB=90°,AB=5,BC=3,点P从点A出发,以每秒2个单位长度的速度沿折线A-C-B-A运动.设点P的运动时间为t秒(t>0).
(1)、求点A的坐标;(2)、若一次函数y1=﹣x﹣2与y2=x﹣4的图象与x轴分别相交于点B、C,求△ABC的面积.(3)、结合图象,直接写出y1≥y2时x的取值范围.24. 如图,在△ABC中,∠ACB=90°,AB=5,BC=3,点P从点A出发,以每秒2个单位长度的速度沿折线A-C-B-A运动.设点P的运动时间为t秒(t>0).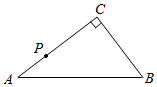 (1)、求AC的长及斜边AB上的高;(2)、当点P在CB上时,CP的长为 . (用含t的代数式表示)(3)、当点P在AC上时,直接写出△BCP是等腰三角形时t的值.25. 在等边 中,点E是AB上的动点,点E与点A、B不重合,点D在CB的延长线上,且 .
(1)、求AC的长及斜边AB上的高;(2)、当点P在CB上时,CP的长为 . (用含t的代数式表示)(3)、当点P在AC上时,直接写出△BCP是等腰三角形时t的值.25. 在等边 中,点E是AB上的动点,点E与点A、B不重合,点D在CB的延长线上,且 .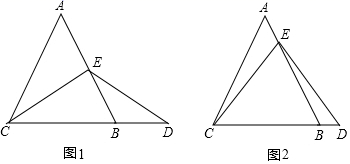 (1)、如图1,若点E是AB的中点,求证: ;(2)、如图2,若点E不是AB的中点时, 中的结论“ ”能否成立?若不成立,请直接写出BD与AE数量关系,若成立,请给予证明.
(1)、如图1,若点E是AB的中点,求证: ;(2)、如图2,若点E不是AB的中点时, 中的结论“ ”能否成立?若不成立,请直接写出BD与AE数量关系,若成立,请给予证明.