云南省曲靖市罗平县2020-2021学年八年级下学期期中数学试题

试卷更新日期：2023-02-28 类型：期中考试

进入出卷网下载

一、单选题

1. 下列说法正确的有几个（）
①两组对角分别相等的四边形是平行四边形；②对角线互相平分的四边形是平行四边形；③对角线相等的平行四边形是矩形；④矩形的四个角是直角；⑤对角线互相垂直的四边形是菱形；⑥对角线互相垂直的平行四边形是菱形；⑦四条边相等的四边形是菱形．

A、6个 B、5个 C、4个 D、7个

查看试题解析
2. 下列各组数中，是勾股数的是（）

A、 $\frac{1}{3} ， \frac{1}{4} ， \frac{1}{5}$ B、3，4，7 C、6，8，10 D、1， $\sqrt{2}$ ， 2

查看试题解析
3. 如图，O为数轴的原点，数轴上点A、B表示的数分别是1和2，CA⊥OA于点A，且AC=OA；DB⊥OB于点B，且DB=OA；以点O为圆心，OC长为半径画弧，交数轴于点E；以点O为圆心，OD长为半径画弧，交数轴于点F；则点E和点F表示的数分别是（）

A、1.4，2.2 B、 $\sqrt{2} ， \sqrt{5}$ C、 $\sqrt{2} ， \sqrt{3}$ D、 $\sqrt{3} ， \sqrt{6}$

查看试题解析
4. 如图，一架梯子斜靠在墙上，设梯子AB的中点为O，AB=6米，BC=2米，若梯子B端沿地面向右滑行1米，则点O到点C的距离（　　）

A、减小1米 B、增大1米 C、始终是2米 D、始终是3米

查看试题解析
5. 当 $\frac{a + 2}{\sqrt{a - 2}}$ 有意义时，a的取值范围是（）

A、a≥2 B、a＞2 C、a≠2 D、a≠－2

查看试题解析
6. 如图：将边长为6的正方形纸片ABCD折叠，使点D落在AB边中点E处，点C落在点Q处，折痕为FH，则线段AF的长是（）

A、2 B、 $\frac{9}{4}$ C、3 D、 $\frac{9}{5}$

查看试题解析
7. 平行四边形ABCD的对角线相交于点O，且AD≠CD，过点O作OM⊥AC，交AD于点M．如果△CDM的周长为6，那么平行四边形ABCD的周长是（）

A、8 B、10 C、12 D、18

查看试题解析
8. 如图，在平行四边形ABCD中对角线AC、BD交于点O，并且∠DAC＝60°，∠ADB＝15°．点E是AD边上一个动点，延长EO交BC于点F，当点E从D点向A点移动过程中（点E与点D，A不重合），则四边形AFCE的变化是（　　）

A、平行四边形→矩形→平行四边形→菱形→平行四边形 B、平行四边形→菱形→平行四边形→矩形→平行四边形 C、平行四边形→矩形→平行四边形→正方形→平行四边形 D、平行四边形→矩形→菱形→正方形→平行四边形

查看试题解析

二、填空题

9.
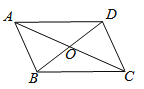
如图，四边形ABCD的对角线相交于点O，AO=CO，请添加一个条件（只添一个即可），使四边形ABCD是平行四边形

查看试题解析
10. 若 $\sqrt{{(4 - m)}^{2}} = 4 - m$ ，则m的取值范围是．

查看试题解析
11. 对于任意不相等的两个正实数a，b，定义运算△如下：如a△b $= \frac{\sqrt{a + b}}{3 - 2}$ ，如3△2 $= \frac{\sqrt{3 + 2}}{3 - 2} = \sqrt{5}$ ，那么8△12＝．

查看试题解析
12. 如图，若▱ABCD的周长为22 cm，AC，BD相交于点O，△AOD的周长比△AOB的周长小3 cm，则AB＝．

查看试题解析
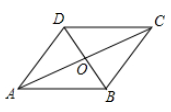13. 如图，将一根25㎝长的细木棒放入长、宽、高分别为8㎝、6㎝和10 $\sqrt{3}$ ㎝的长方体无盖盒子中，则细木棒露在盒外面的最短长度是㎝．

查看试题解析
14. 如图，已知△ABC是腰长为1的等腰直角三角形，以Rt△ABC的斜边AC为直角边，画第2个等腰Rt△ACD，再以Rt△ACD的斜边AD为直角边，画第3个等腰Rt△ADE，…，依此类推，则第2018个等腰直角三角形的斜边长是．

查看试题解析

三、解答题

15. 计算：

(1)、（5 $\sqrt{48} - 6 \sqrt{27} + 4 \sqrt{15}$ ） $+ \sqrt{3}$ ；

(2)、（ $\sqrt{8} + \sqrt{3}$ ） $\times \sqrt{6} -$ （4+8 $\sqrt{6}$ ）÷2 $\sqrt{2}$ ．

查看试题解析
16. 先化简，再求值： $(1 - \frac{1}{a + 1}) \cdot \frac{a^{2} + 2 a + 1}{a}$ ，其中a ＝ $\sqrt{2}$ －1.

查看试题解析
17. 如图，已知网格上最小的正方形的边长为 $1$ （长度单位），点 $A 、 B 、 C$ 在格点上.

(1)、直接在平面直角坐标系中作出 $△ A B C$ 关于 $y$ 轴对称的图形 $△ A_{1} B C_{1}$ （点 $A$ 对应点 $A_{1}$ ，点 $C$ 对应点 $C_{1}$ ）；

(2)、 $△ A B C$ 的面积为（面积单位）（直接填空）；

(3)、点 $B$ 到直线 $A_{1} C_{1}$ 的距离为（长度单位）（直接填空）；

查看试题解析
18. 某中学有一块四边形的空地ABCD，如图所示，学校计划在空地上种植草皮，经测量∠B=90°，AB=3m，BC=4m，CD=12m，AD=13m.若每平方米草皮需要200元，问学校需要投入多少资金买草皮？

查看试题解析
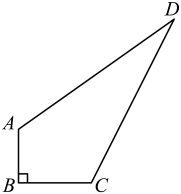19. 观察下列式子：

(1)、 $\sqrt{2 + \frac{2}{3}} = 2 \sqrt{\frac{2}{3}}$ ，（2） $\sqrt{3 + \frac{3}{8}} = 3 \sqrt{\frac{3}{8}}$ ，（3） $\sqrt{4 + \frac{4}{15}} = 4 \sqrt{\frac{4}{15}}$ ……，
你能发现其中的规律吗？请你用含n的式子表示这一规律表示，并给出证明．

查看试题解析
20. 如图所示，已知直线MN//PQ，直线AC交MN、PQ于点A、C，所得的同旁内角的平分线AB、BC和AD、CD分别相交于点B、D．试猜想AC与BD的关系，并说明理由．

查看试题解析
21. 如图，一架2.5米长的梯子AB斜靠在竖直的墙AC上，这时梯子底部B到墙底端的距离为0.7米，考虑爬梯子的稳定性，现要将梯子顶部A沿墙下移0.4米到A′处，问梯子底部B将外移多少米？

查看试题解析
22. 已知，如图，CD是Rt△FBE的中位线，A是EB延长线上一点，且AB= $\frac{1}{2}$ BE．

(1)、证明：四边形ABCD是平行四边形；

(2)、若∠E=60°，AD=3cm，求BE的长．

查看试题解析
23. 如图，在 $R t △ A B C$ 中， $∠ B = 90 °$ ， $A C = 60 c m$ ， $∠ A = 60 °$ ，点D从点C出发沿CA方向以 $4 c m / s$ 的速度向点A匀速运动，同时点E从点A出发沿AB方向以 $2 c m / s$ 的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D、E运动的时间是t秒（ $0 < t \leq 15$ ）．过点D作 $D F ⊥ B C$ 于点F，连接DE，EF．

(1)、求证： $A E = D F$ ；

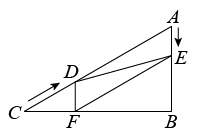(2)、四边形 $A E F D$ 能够成为菱形吗？如果能，求出相应的t值，如果不能，说明理由；

(3)、当t为何值时， $△ D E F$ 为直角三角形？请说明理由．

查看试题解析