辽宁省葫芦岛市连山区2021-2022学年八年级下学期期中数学试题

试卷更新日期：2023-02-28 类型：期中考试

进入出卷网下载

一、单选题

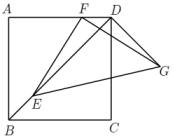
1. 若 $\sqrt{a^{3} + 2 a^{2}} = - a \sqrt{a + 2}$ ，则a的取值范围是（）

A、 $- 2 \leq a \leq 0$ B、 $a \leq 0$ C、 $a < 0$ D、 $a \geq - 2$

查看试题解析
2. 下列二次根式中，最简二次根式是（）

A、 $\sqrt{a^{2} + b^{2}}$ B、 $\sqrt{0.1 a}$ C、 $\sqrt{a^{2} b}$ D、 $\sqrt{\frac{a}{b}}$

查看试题解析
3. 平行四边形一边长是10cm，那么它的两条对角线的长度可以是（　　）

A、8cm和6cm B、8cm和8cm C、8cm和12cm D、8cm和16cm

查看试题解析
4. 如图所示，E，F，G，H为四边形 $A B C D$ 各边的中点，若对角线 $A C ， B D$ 的长都为20，则四边形 $E F G H$ 的周长是（）

A、80 B、40 C、20 D、10

查看试题解析
5. 如图，在▱ABCD中，BE⊥AB交对角线AC于点E．若∠1＝20°，则∠2的度数为（）

A、120° B、100° C、110° D、90°

查看试题解析
6. 如图，在直角三角形 $A B C$ 中， $∠ A C B = 90 °$ ， $A C = 3$ ， $B C = 4$ ，点M是边 $A B$ 上一点（不与点A，B重合），作 $M E ⊥ A C$ 于点E， $M F ⊥ B C$ 于点F，则 $E F$ 的最小值是（）

A、2 B、2.4 C、2.5 D、2.6

查看试题解析
7. 如果 $a b > 0$ ， $a + b < 0$ 那么下面各式： $① \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} ； ② \sqrt{\frac{a}{b}} \cdot \sqrt{\frac{b}{a}} = 1 ； ③ \sqrt{a b} \div \sqrt{\frac{a}{b}} = - b ；$ 其中正确的是（）

A、①② B、①③ C、①②③ D、②③

查看试题解析
8. 已知点P的坐标是 $(1 ， 1)$ ，点Q的坐标是 $(5 ， 2)$ ， A为x轴上的动点，则 $A P + A Q$ 的最小值是（）

A、4 B、5 C、6 D、8

查看试题解析
9. 如图，直线l上方摆放五个正方形，从左往右数，一、三、五的面积分别是 $S_{1} = 4 ， S_{3} = 6 ， S_{5} = 8$ ，则二、四的面积和 $S_{2} + S_{4}$ 等于（）

A、18 B、20 C、22 D、24

查看试题解析
10. 如图，E，D分别在△ABC的边AC，BC上，AD⊥BE，垂足为点F，AF=3DF，BF=3EF，AE=2 $\sqrt{6}$ ， BD=4，则AB=（）

A、4 B、5 C、6 D、8

查看试题解析

二、填空题

11. 计算 $3 \sqrt{\frac{1}{3}}$ 的结果是．

查看试题解析
12. 计算：（ $\sqrt{5}$ ）²=

查看试题解析
13. 在△ABC中，AB=AC=5，BC=6，则△ABC的面积是．

查看试题解析
14. 如图，在矩形OBAC中，点A的坐标为(5，12)，则BC的长是．

查看试题解析
15. 如图，矩形ABCD中，点E在BC上，且AE平分∠BAC，AE=CE，BE=2，则矩形ABCD的面积为．

查看试题解析
16. 已知△ABC中，AB＝17，AC＝10，BC边上的高AD＝8．则边BC的长为．

查看试题解析
17. 如图，点E，点F在正方形ABCD的内部，AE=CF=4，EF=6，∠E=∠F=90°，则正方形ABCD的面积是．

查看试题解析
18. 如图，E，F分别是边长为4的正方形 $A B C D$ 的边 $A D$ ， $D C$ 上的动点，满足 $A E = D F$ ，连接 $A F$ ， $B E$ ， $B E$ 与 $A F$ 相交于点P，连接 $D P$ ，则 $D P$ 的最小值是．

查看试题解析

三、解答题

19. 计算：

(1)、 $\sqrt{12} - \sqrt{18} + 3 \sqrt{\frac{1}{3}} + \sqrt{8}$ ；

(2)、 $(\sqrt{6} - 2 \sqrt{15}) \cdot \sqrt{3} - 6 \sqrt{\frac{1}{2}} + 3 \sqrt{20}$ ．

查看试题解析
20. 已知 $x = 4 - \sqrt{3}$ ，求代数式 $x^{2} + (2 + \sqrt{3}) x - 24$ 的值．

查看试题解析
21. 如图，折叠矩形纸片ABCD，先折出折痕BD，再折叠使AD边与对角线BD重合，得折痕DE，AB=4，BC=3．

(1)、求BD的长；

(2)、求 $A E$ 的长，

查看试题解析
22.
已知：如图四边形ABCD是平行四边形，P、Q是直线AC上的点，且AP=CQ．
求证：四边形PBQD是平行四边形．

查看试题解析
23. 如图，在四边形ABCD中，AD $∥$ BC，AB=BC，对角线AC，BD交于点O，BD平分∠ABC，过点D作DE⊥BC，交BC的延长线于点E，连接OE．

(1)、求证：四边形 $A B C D$ 是菱形；

(2)、若 $C D = 17$ ， $A C = 16$ ，求 $O E$ 的长．

查看试题解析
24. 如图，以△ABC的边AB，AC为边在△ABC的外部作正方形ABEF与正方形ACGD，连接BD，CF，DF，CF交BD于O，交AD于H．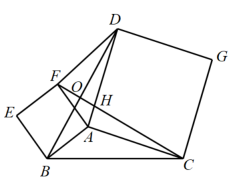

(1)、写出CF与BD的数量关系和位置关系，并说明理由；

(2)、若AB=2，AC=4，直接写出BC²+DF²的值．

查看试题解析
25. 如图，在四边形 $A B C D$ 中， $A D ∥ B C$ ， $∠ B = 90 °$ ， $A B = 4 c m$ ， $A D = 8 c m$ ， $B C = 11 c m$ ，点P从点A出发，以 $1 c m / s$ 的速度向点D运动；点Q从点C同时出发，以 $1 c m / s$ 的速度向点B运动、规定其中一个动点到达端点时，另一个动点也随之停止运动．设点P，Q运动的时间为 $t s$ ．

(1)、 $C D$ 边的长度为；

(2)、从运动开始，当t取何值时， $P Q = C D$ ？

(3)、是否存在t，使得 $△ D P Q$ 是直角三角形？若存在，直接写出t值；若不存在，请说明理由．

查看试题解析
26. 如图，在正方形 $A B C D$ 中，E，F分别在 $B D$ ， $A D$ 上，连接 $E F$ ，在 $E F$ 的右侧作等腰直角三角形 $E F G$ ，使 $∠ E F G = 90 °$ ，连接 $D G$ ．

(1)、求证： $D G ⊥ B D$ ；

(2)、若 $A B = 8$ ， $F D = 2$ ， $B E = 2 \sqrt{2}$ ，直接写出线段 $D G$ 的长．

查看试题解析