辽宁省大连市金普新区2021-2022学年下学期八年级数学期中试卷

试卷更新日期：2023-02-28 类型：期中考试

进入出卷网下载

一、单选题

1. 二次根式 $\sqrt{x - 1}$ 有意义的x的范围是（）

A、 $x = 1$ B、 $x \neq 1$ C、 $x ≥ 1$ D、 $x \leq 1$

查看试题解析
2. $\sqrt{2}$ 的倒数是（）．

A、 $- \sqrt{2}$ B、 $- \frac{\sqrt{2}}{2}$ C、 $- 2$ D、 $\frac{\sqrt{2}}{2}$

查看试题解析
3. 下列二次根式中，最简二次根式是（）．

A、 $\sqrt{\frac{1}{3}}$ B、 $\sqrt{3}$ C、 $\sqrt{9}$ D、 $\sqrt{27}$

查看试题解析
4. 下列计算正确的是（）．

A、 $\sqrt{4} = \pm 2$ B、 $\sqrt{{(- 3)}^{2}} = - 3$ C、 $\sqrt{4} - \sqrt{2} = \sqrt{2}$ D、 $\sqrt{2} \times \sqrt{3} = \sqrt{6}$

查看试题解析
5. 在平面直角坐标系中，下列函数的图象经过点 $(1 ， 2)$ 的是（）．

A、 $y = - 2 x$ B、 $y = - \frac{2}{x}$ C、 $y = - 4 x + 6$ D、 $y = 3 x^{2} - 5$

查看试题解析
6. 平面直角坐标系中，点A坐标为 $(0 ， - 3)$ ， B是x轴正半轴上一点， $A B = 5$ ，则点B的坐标是（）．

A、 $(4 ， 0)$ B、 $(0 ， 4)$ C、 $(\sqrt{34} ， 0)$ D、 $(0 ， \sqrt{34})$

查看试题解析
7. 下列各组数中能作为直角三角形的三边长的是（）．

A、1， $\sqrt{2}$ ， $\sqrt{3}$ B、 $\sqrt{3}$ ， $\sqrt{4}$ ， $\sqrt{5}$ C、2，3，4 D、6，7，8

查看试题解析
8. $P_{1} (- 6 ， y_{1})$ ， $P_{2} (8 ， y_{2})$ 是正比例函数 $y = k x (k < 0)$ 的图上的两个点，则 $y_{1}$ ， $y_{2}$ 的大小关系是（）．

A、 $y_{1} > y_{2}$ B、 $y_{1} < y_{2}$ C、 $y_{1} = y_{2}$ D、不能确定

查看试题解析
9. 下列不能判定四边形ABCD是平行四边形的条件是（）．

A、 $A B = C D$ ， $A D = B C$ B、 $A B = C D$ ， $A B ∥ C D$ C、 $A B = C D$ ， $A D ∥ B C$ D、 $A D = B C$ ， $A D ∥ B C$

查看试题解析
10. 顺次连接菱形四边中点得到的四边形是（）

A、平行四边形 B、菱形 C、矩形 D、正方形

查看试题解析

二、填空题

11. 在平行四边形ABCD中， $∠ A + ∠ C = 120 °$ ，则 $∠ A =$ °．

查看试题解析
12. 正方形边长为6，若边长增加x，则面积增加y，y关于x的函数解析式为．

查看试题解析
13. 菱形的边长为5，一条对角线长为8，则此菱形的面积是．

查看试题解析
14. 观察下列各式 $\sqrt{2 \frac{2}{3}} = 2 \sqrt{\frac{2}{3}} ， \sqrt{3 \frac{3}{8}} = 3 \sqrt{\frac{3}{8}} ， \sqrt{4 \frac{4}{15}} = 4 \sqrt{\frac{4}{15}}$ ……．用含有字母n的式子表示

查看试题解析
15. 如图，在Rt△ABC中，∠ACB＝90°，D、E、F分别是AB、BC、CA的中点，若CD＝8，则EF＝．

查看试题解析

三、填空题

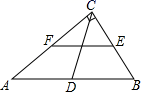
16. 如图， $△ A B C$ 中，AD是BC边上的高， $∠ C A D = \frac{1}{2} ∠ A B C$ ， E是AB的中点，若 $A D = h$ ， $D E = m$ ，则CD的长为．

查看试题解析

四、解答题

17. 一次函数y=kx+b，当x=1时，y=5；当x=-1时，y=1．求k和b的值．

查看试题解析
18. 计算： $(\sqrt{5} + 1) (\sqrt{5} - 1) + {(\sqrt{3} + 1)}^{2} - \frac{6}{\sqrt{3}}$ ．

查看试题解析
19. 已知：如图，在平行四边形ABCD中，点E、F在AC上，且AE＝CF.求证：BE＝DF.

查看试题解析
20.
如图，一个梯子AB长2.5米，顶端A靠在墙AC上，这时梯子下端B与墙角C距离为1.5米，梯子滑动后停在DE的位置上，测得BD长为0.5米，求梯子顶端A下落了多少米？

查看试题解析
21. 有一块木板(图中阴影部分)，测得 $A B = 4$ ， $B C = 3$ ， $D C = 12$ ， $A D = 13$ ， $∠ A B C = 90 °$ ．求阴影部分面积．

查看试题解析
22. 已知矩形ABCD，点E是直线CD上任意一点，过点C作 $C F ⊥ A E$ ，垂足为F，连接BF，DF．

(1)、如图1，当点E在线段CD上时，写出线段BF与DF的位置关系并证明；

(2)、如图2．当点E在线段CD延长线上时，补全图形，写出线段BF与DF的位置关系并证明．

查看试题解析
23. 如图，已知 $△ A B C$ 中 $∠ B A C = 45 °$ ， $A D ⊥ B C$ ，垂足为D， $B D = 2$ ， $D C = 3$ ，求AD的长．小明同学将图形进行翻折，请按照小明的思路，探究并解答下列问题：

(1)、分别以AB、AC为对称轴，画出 $△ A B D$ 、 $△ A C D$ 的轴对称图形，D点的对称点为E、F，延长EB、FC相交于点G．证明四边形AEGF是正方形；

(2)、求AD的长．

查看试题解析
24. 菱形ABCD中， $∠ B A D = 120 °$ ， E，F分别是射线BC，CD上一点， $∠ E A F = 60 °$ ．

(1)、如图1，当点E，F分别在线段BC，CD上时，写出线段BE，DF，AB之间的数量关系并证明；

(2)、如图2，当点E，F分别在线段BC，CD延长线上时，写出线段BE，DF，AB之间的数量关系并证明；

查看试题解析
25. 如图， $△ A B C$ 中， $A C = B C$ ， $∠ A C B = 90 °$ ，点D、E在AB上，且 $A D = B E$ ， $E F ⊥ C D$ ，垂足为F，EF的延长线与AC相交于点G．

(1)、在图中找出与线段CD相等的线段，并证明；

(2)、写出线段AE，BE，EG之间的数量关系，并证明．

查看试题解析
26. 如图，点E为正方形ABCD外一点， $∠ A E B = 45 °$ ，连接DE．

(1)、写出线段BE与DE的位置关系并证明；

(2)、写出线段AE，BE，DE之间的数量关系并证明．

查看试题解析