黑龙江省佳木斯市抚远市2021-2022学年八年级下学期期中数学试题
试卷更新日期:2023-02-28 类型:期中考试
一、单选题
-
1. 下列属于最简二次根式的是( )A、 B、 C、 D、2. 下列各组数能作为直角三角形的三边长的是( )A、7,8,9 B、9,12,15 C、4,5,6 D、 , ,3. 下列各式中,运算正确的是( )A、=﹣2 B、+= C、×=4 D、2﹣4. 矩形具有而平行四边形不一定具有的性质是( )A、对边相等 B、对角相等 C、对角线相等 D、对角线互相平分5. 实数a,b在数轴上的位置如图所示,则化简 - +b的结果是( )
 A、1 B、b+1 C、2a D、1-2a6. 如图所示,在正方形ABCD中,E是对角线AC上的一点.连接BE,且 , 则∠EBC的度数是( )
A、1 B、b+1 C、2a D、1-2a6. 如图所示,在正方形ABCD中,E是对角线AC上的一点.连接BE,且 , 则∠EBC的度数是( ) A、45° B、30° C、22.5° D、20°7. 如图,在菱形ABCD中,对角线AC,BD相交于点O,已知 , , 则菱形ABCD的面积为( )
A、45° B、30° C、22.5° D、20°7. 如图,在菱形ABCD中,对角线AC,BD相交于点O,已知 , , 则菱形ABCD的面积为( ) A、96 B、48 C、36 D、388. △ABC中,∠A,∠B,∠C所对的边分别是a,b,c下列条件中不能说明△ABC是直角三角形的是( )A、b2- c2=a2 B、a:b:c= 5:12:13 C、∠A:∠B:∠C = 3:4:5 D、∠C =∠A -∠B9. 已知 , 则的值为( )A、8 B、9 C、11 D、1210. 已知:如图,在正方形ABCD外取一点E,连接AE,BE,DE,过点A作AE的垂线交DE于点P.若AE=AP=1,PB= . 下列结论:①△APD≌△AEB;②点B到直线AE的距离为;③EB⊥ED;④S△APD+S△APB=1+ . 其中正确结论的序号是( )
A、96 B、48 C、36 D、388. △ABC中,∠A,∠B,∠C所对的边分别是a,b,c下列条件中不能说明△ABC是直角三角形的是( )A、b2- c2=a2 B、a:b:c= 5:12:13 C、∠A:∠B:∠C = 3:4:5 D、∠C =∠A -∠B9. 已知 , 则的值为( )A、8 B、9 C、11 D、1210. 已知:如图,在正方形ABCD外取一点E,连接AE,BE,DE,过点A作AE的垂线交DE于点P.若AE=AP=1,PB= . 下列结论:①△APD≌△AEB;②点B到直线AE的距离为;③EB⊥ED;④S△APD+S△APB=1+ . 其中正确结论的序号是( ) A、①②③ B、①②④ C、②③④ D、①③④
A、①②③ B、①②④ C、②③④ D、①③④二、填空题
-
11. 若代数式 有意义,则x的取值范围是.12. 如图,已知四边形ABCD的对角线AC与BD相交于点O, , 添加一个条件 , 使四边形ABCD为平行四边形(填一个即可).
 13. 直角三角形斜边长是5,一直角边的长是3,则此直角三角形的面积为 .14. 若是一个整数.则n可取的最小正整数是 .15.
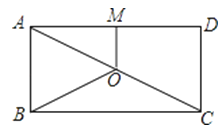
13. 直角三角形斜边长是5,一直角边的长是3,则此直角三角形的面积为 .14. 若是一个整数.则n可取的最小正整数是 .15.如图,O是矩形ABCD的对角线AC的中点,M是AD的中点.若AB=5,AD=12,则四边形ABOM的周长为 .
 16. 如图,在中, , 连接BD,作交CD的延长线于点E,过点E作交BC的延长线于点F,且 , 则边AB的长是 .
16. 如图,在中, , 连接BD,作交CD的延长线于点E,过点E作交BC的延长线于点F,且 , 则边AB的长是 . 17. 把根号外的因式移到根号内,得.18.
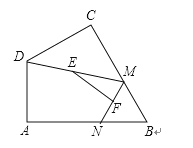
17. 把根号外的因式移到根号内,得.18.如图,四边形ABCD中,∠A=90°,AB=3 , AD=3,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为 .
 19. 在Rt△ABC中,∠A,∠B,∠C所对的边分别为a,b,c,a∶b=2∶3,c= ,则a=.20. 如图,在正方形ABCB1中,AB=1,AB与直线l的夹角为30°,延长交直线l于点 , 作正方形 , 延长交直线l于点 , 作正方形 , 延长交直线l于点 , 作正方形……以此类推, .
19. 在Rt△ABC中,∠A,∠B,∠C所对的边分别为a,b,c,a∶b=2∶3,c= ,则a=.20. 如图,在正方形ABCB1中,AB=1,AB与直线l的夹角为30°,延长交直线l于点 , 作正方形 , 延长交直线l于点 , 作正方形 , 延长交直线l于点 , 作正方形……以此类推, .
三、解答题
-
21. 计算:(1)、;(2)、 .22. 先化简.再求值: , 其中 , .23. 已知的三边长为a,b,c,且满足 . 试判断的形状,并说明理由.24. 如图,在中, , , , D,E,F分别是边AB,BC,AC的中点,连接DE,DF,EF,的度数为53°.
 (1)、求∠C的度数;(2)、求四边形ADEF的周长.25. 如图,在▱ABCD中,AC交BD于点O , 点E,点F分别是OA,OC的中点。求证:四边形BEDF为平行四边形
(1)、求∠C的度数;(2)、求四边形ADEF的周长.25. 如图,在▱ABCD中,AC交BD于点O , 点E,点F分别是OA,OC的中点。求证:四边形BEDF为平行四边形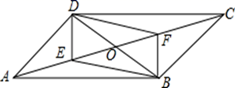 26. 如图,在矩形ABCD中,对角线AC与BD相交于点O,过点C作BD的平行线,过点D作AC的平行线,两线交于点P.
26. 如图,在矩形ABCD中,对角线AC与BD相交于点O,过点C作BD的平行线,过点D作AC的平行线,两线交于点P. (1)、求证:四边形CODP是菱形:(2)、若 , , 求四边形CODP的面积.27. 在正方形ABCD中,点E,F分别在边AD,DC所在直线上,连接EF,BE,BF,过点B作BP⊥EF交EF于点P,且∠EBC=∠BEF.
(1)、求证:四边形CODP是菱形:(2)、若 , , 求四边形CODP的面积.27. 在正方形ABCD中,点E,F分别在边AD,DC所在直线上,连接EF,BE,BF,过点B作BP⊥EF交EF于点P,且∠EBC=∠BEF. (1)、如图①,当点E,F分别在AD,DC边上时,求证:;(2)、如图②,当点E,F分别在边AD,DC的延长线上时;如图③,当点E,F分别在边DA,CD的延长线上时,线段AE,CF,EF有怎样的数量关系?请写出你的猜想.不需要证明.28. 如图,在平面直角坐标系中,点A在y轴的正半轴上,点B在x轴的正半轴上,且OA,OB的长满足式子 , AE平分 , 将沿AE所在直线翻折,使点O落在边AB上的点D处.
(1)、如图①,当点E,F分别在AD,DC边上时,求证:;(2)、如图②,当点E,F分别在边AD,DC的延长线上时;如图③,当点E,F分别在边DA,CD的延长线上时,线段AE,CF,EF有怎样的数量关系?请写出你的猜想.不需要证明.28. 如图,在平面直角坐标系中,点A在y轴的正半轴上,点B在x轴的正半轴上,且OA,OB的长满足式子 , AE平分 , 将沿AE所在直线翻折,使点O落在边AB上的点D处. (1)、求A,B两点的坐标及AB的长;(2)、点E到直线AB的距离为;(3)、在坐标平面内是否存在一点P,使以A,E,B,P为顶点的四边形为平行四边形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
(1)、求A,B两点的坐标及AB的长;(2)、点E到直线AB的距离为;(3)、在坐标平面内是否存在一点P,使以A,E,B,P为顶点的四边形为平行四边形?若存在,请直接写出点P的坐标;若不存在,请说明理由.