黑龙江省大庆市龙凤区2021-2022学年八年级下学期期中数学试题
试卷更新日期:2023-02-28 类型:期中考试
一、单选题
-
1. 下列方程是一元二次方程的是( )A、 B、 C、 D、2. 下列两个图形一定相似的是( )A、两个正方形 B、两个等腰三角形 C、两个直角三角形 D、两个菱形3. 下列说法:
⑴对角线互相垂直的四边形是菱形;
⑵对角线相等的平行四边形是矩形;
⑶对角线互相垂直平分的四边形是正方形;
⑷两组对角相等的四边形是平行四边形;
其中正确的有( )个.
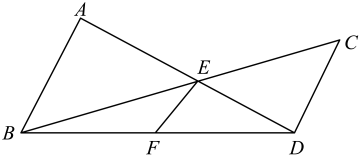
A、1 B、2 C、3 D、44. 如图, , 若 , , 等于( )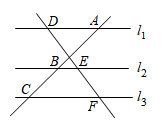 A、 B、 C、 D、5. 顺次连接四边形各边中点得到四边形 , 要使四边形是矩形,需要添加的条件是( )A、 B、 C、 D、6. 实数a,b,c满足4a﹣2b+c=0,则( )A、b2﹣4ac>0 B、b2﹣4ac≥0 C、b2﹣4ac<0 D、b2﹣4ac≤07. 已知 , 则x的值为( )A、-1 B、-1或1 C、-1或 D、8. 志愿者是自愿贡献个人的时间和精力,在不计物质报酬的前提下头推动人类发展、社会进步和社会福利事业而提供服务的人员.某医院要从A、B、C三名志愿者中任意抽调两人助力全民核酸检测工作,恰好抽到志愿者B 和C的概率是( )A、 B、 C、 D、9. 一个五边形ABCDE各边的边长为2,3,4,5,6,另一个和它相似的五边形A1B1C1D1E1最长边为12,则A1B1C1D1E1的最短边长为( )A、8 B、6 C、4 D、210. 如图,在Rt△ABC中,∠BAC=90°,AC=9,AB=12,中线AD与角平分线BE相交于点F,则线段AF的长为( )
A、 B、 C、 D、5. 顺次连接四边形各边中点得到四边形 , 要使四边形是矩形,需要添加的条件是( )A、 B、 C、 D、6. 实数a,b,c满足4a﹣2b+c=0,则( )A、b2﹣4ac>0 B、b2﹣4ac≥0 C、b2﹣4ac<0 D、b2﹣4ac≤07. 已知 , 则x的值为( )A、-1 B、-1或1 C、-1或 D、8. 志愿者是自愿贡献个人的时间和精力,在不计物质报酬的前提下头推动人类发展、社会进步和社会福利事业而提供服务的人员.某医院要从A、B、C三名志愿者中任意抽调两人助力全民核酸检测工作,恰好抽到志愿者B 和C的概率是( )A、 B、 C、 D、9. 一个五边形ABCDE各边的边长为2,3,4,5,6,另一个和它相似的五边形A1B1C1D1E1最长边为12,则A1B1C1D1E1的最短边长为( )A、8 B、6 C、4 D、210. 如图,在Rt△ABC中,∠BAC=90°,AC=9,AB=12,中线AD与角平分线BE相交于点F,则线段AF的长为( ) A、 B、 C、5 D、2
A、 B、 C、5 D、2二、填空题
-
11. 一个周长为 的三角形,由它的三条中位线构成的三角形的周长为 .12. 把10cm长的线段进行黄金分割后得两条线段,其中较长的线段的长为cm .13. 如图,一块飞镖游戏板由大小相等的小正方形格子构成,向游戏板随机投掷一枚飞镖,击中黑色区域的概率是 .
 14. 关于的一元二次方程 . 王同学由于看错了二次项系数,误求得两根为2和4,那么 .15. 如图,已知菱形的面积为24,正方形的面积为18,则菱形的边长是 .
14. 关于的一元二次方程 . 王同学由于看错了二次项系数,误求得两根为2和4,那么 .15. 如图,已知菱形的面积为24,正方形的面积为18,则菱形的边长是 .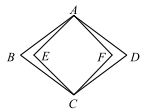 16. 已知关于 的一元二次方程 ,有下列结论:
16. 已知关于 的一元二次方程 ,有下列结论:①当 时,方程有两个不相等的实根;
②当 时,方程不可能有两个异号的实根;
③当 时,方程的两个实根不可能都小于1;
④当 时,方程的两个实根一个大于3,另一个小于3.
以上4个结论中,正确的个数为 .
17. 如图,在△ABC中,D,E分别是BC,AC的中点,AD与BE相交于点G,若DG=1,则AD=. 18. 如图,矩形ABCD中,AB=8,BC=4,点E在边AB上,点F在边CD上,点G、H在对角线AC上,若四边形EGFH是菱形,则AE的长是 .
18. 如图,矩形ABCD中,AB=8,BC=4,点E在边AB上,点F在边CD上,点G、H在对角线AC上,若四边形EGFH是菱形,则AE的长是 .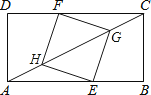
三、解答题
-
19. 解方程:(1)、(2)、20. 一个不透明的袋子中装有若干个除颜色外均相同的小球,小明每次从袋子中摸出一个球,记录下颜色,然后放回,重复这样的试验1000次,记录结果如下:
实验次数n
200
300
400
500
600
700
800
1000
摸到红球次数m
151
221
289
358
429
497
571
702
摸到红球频率
0.75
0.74
0.72
0.72
0.72
0.71
a
b
(1)、表格中a=;b=;(精确到0.01)(2)、估计从袋子中摸出一个球恰好是红球的概率约为 ;(精确到0.1)(3)、如果袋子中有14个红球,1个白球,若干黄球,估计袋子中黄球的个数和摸到黄球的概率?21. 某学校去年年底的绿化面积为2500平方米,预计到明年年底增加到3600平方米,若这两年的平均增长率相同,求这两年的平均增长率.22. 某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件.求:(1)、若商场平均每天要盈利1200元,每件衬衫应降价多少元?(2)、每件衬衫降价多少元时,商场平均每天盈利最多?23. 如图,点D是△ABC的边AB上一点,∠ABC=∠ACD.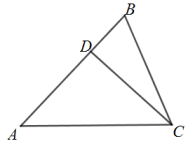 (1)、求证:△ABC∽△ACD;(2)、当AD=2,AB=3时,求AC的长.24. 如图,正方形ABCD的对角线AC、BD相交于点O,将BD向两个方向延长,分别至点E和点F,且使BE=DF.
(1)、求证:△ABC∽△ACD;(2)、当AD=2,AB=3时,求AC的长.24. 如图,正方形ABCD的对角线AC、BD相交于点O,将BD向两个方向延长,分别至点E和点F,且使BE=DF.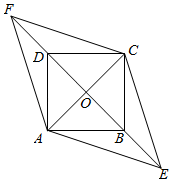 (1)、判断四边形AECF的形状,并证明你的猜想;(2)、若AB=3 , BE=3,求四边形AECF的周长.25. 如图,有一块三角形土地,它的底边m,高m,某单位要沿底边BC建一座是矩形的大楼,且使矩形的两个端点D、G分别在AB、AC上,当这座大楼的地基面积为1875时,求这个矩形沿BC边所占的EF的长.
(1)、判断四边形AECF的形状,并证明你的猜想;(2)、若AB=3 , BE=3,求四边形AECF的周长.25. 如图,有一块三角形土地,它的底边m,高m,某单位要沿底边BC建一座是矩形的大楼,且使矩形的两个端点D、G分别在AB、AC上,当这座大楼的地基面积为1875时,求这个矩形沿BC边所占的EF的长. 26. 如图所示,△ABC中,∠C=90°,BC=8cm,AC:AB=3:5,点P从点B出发沿BC向点C以2cm/s的速度移动,点Q从点C出发沿CA向点A以1cm/s的速度移动,如果P、Q分别从B、C同时出发:
26. 如图所示,△ABC中,∠C=90°,BC=8cm,AC:AB=3:5,点P从点B出发沿BC向点C以2cm/s的速度移动,点Q从点C出发沿CA向点A以1cm/s的速度移动,如果P、Q分别从B、C同时出发: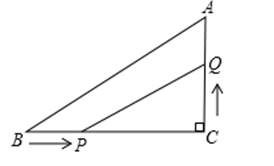 (1)、经过多少秒后,△CPQ的面积为8cm?(2)、经过多少秒时,以C、P、Q为顶点的三角形恰与△ABC相似?
(1)、经过多少秒后,△CPQ的面积为8cm?(2)、经过多少秒时,以C、P、Q为顶点的三角形恰与△ABC相似?