安徽省芜湖市市区2021-2022学年八年级下学期期中考试数学试题

试卷更新日期：2023-02-28 类型：期中考试

进入出卷网下载

一、单选题

1. 下列式子中，一定是二次根式的是（）

A、 $\sqrt{a}$ B、 $\sqrt{a + 1}$ C、 $\sqrt{a - 1}$ D、 $\sqrt{a^{2} + 1}$

查看试题解析
2. 下列二次根式中，不能与 $\sqrt{2}$ 合并的是（　　）

A、 $\sqrt{\frac{1}{2}}$ B、 $\sqrt{8}$ C、 $\sqrt{12}$ D、 $\sqrt{18}$

查看试题解析
3. 下列运算正确的是（）

A、 $\sqrt{2}$ + $\sqrt{3}$ = $\sqrt{5}$ B、 $\sqrt{18}$ =2 $\sqrt{3}$ C、 $\sqrt{2}$ • $\sqrt{3}$ = $\sqrt{5}$ D、 $\sqrt{2}$ ÷ $\sqrt{\frac{1}{2}}$ =2

查看试题解析
4. 在直角坐标系中，点P(2，3)到原点的距离是（）

A、 $\sqrt{5}$ B、 $\sqrt{13}$ C、 $\sqrt{11}$ D、2

查看试题解析
5. 如果三角形的三边分别为 $\sqrt{2}$ ， $\sqrt{6}$ ， 2，那么这个三角形的最大角的度数为（）

A、30° B、45° C、60° D、90°

查看试题解析
6. 如图，点E在平行四边形ABCD的对角线BD上，试判断 $S_{1}$ 与 $S_{2}$ 之间的大小关系（）

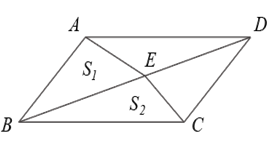A、 $S_{1} = S_{2}$ B、 $S_{1} > S_{2}$ C、 $S_{1} < S_{2}$ D、无法确定

查看试题解析
7. ▱ABCD中，E、F是对角线BD上不同的两点，下列条件中，不能得出四边形AECF一定为平行四边形的是（　　）

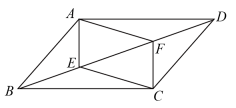A、BE＝DF B、AF∥CE C、CE＝AF D、∠DAF＝∠BCE

查看试题解析
8. 如图，在 $△ A B C$ 中，∠BAC=120°，点D为BC的中点，点E是AC上的一点，且 $A B + A E = E C$ ．若 $D E = 2$ ，则AB的长为（）

A、 $2 \sqrt{3}$ B、4 C、 $3 \sqrt{3}$ D、6

查看试题解析
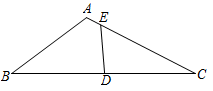9. 如图①，分别以Rt△PMN（MN＞NP）的三边为斜边向外作三个等腰直角三角形，再按图②的方式将两个较小的等腰直角三角形放在最大的等腰直角三角形内，则下列结论不成立的是（）

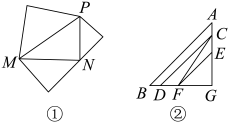A、CF＝AG B、以EF，CD，AB为三边的三角形是直角三角形 C、AE＋CG＝AB D、四边形ABDC的面积与△EFG的面积相等

查看试题解析
10. 在面积为 $6 \sqrt{21}$ 的平行四边形ABCD中，分别过点A作直线BC的垂线AE，垂足为E，作直线CD的垂线AF，垂足为F．若AB＝ $3 \sqrt{7}$ ， BC＝ $2 \sqrt{7}$ ，则CE+CF的值为（）

A、 $5 \sqrt{7} + 10$ B、 $5 \sqrt{7} - 10$ C、 $5 \sqrt{7} + 10$ 或 $2 + \sqrt{7}$ D、 $5 \sqrt{7} + 10$ 或 $5 \sqrt{7} - 10$

查看试题解析

二、填空题

11. 化简： $\sqrt{{(- 2022)}^{2}} =$ ．

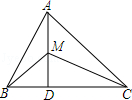
查看试题解析
12. 如图，已知△ABC中，AB=6，AC=9，AD⊥BC于D，M为AD上任一点，则MC²-MB²= ．

查看试题解析
13. 如图，在▱ABCD中，∠ABC＝60°，E，F分别在AD，BA的延长线上，CE∥BD，EF⊥AB，BC＝1，则EF的长为．

查看试题解析
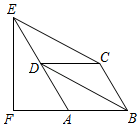14. 如图1，在△ABC中，AB＝ $4 \sqrt{2}$ ， ∠B＝45°，∠C＝60°．

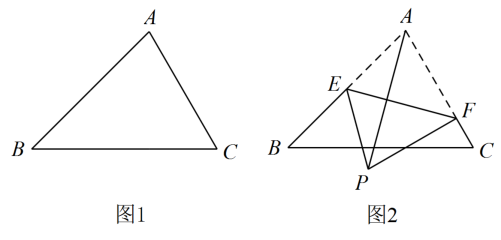(1)、边AC的长为；

(2)、如图2所示，点E为边AB的中点，点F在边AC上，连结EF，将△AEF沿EF折叠得到△PEF．连结AP，当PF⊥AC时，AP的长为．

查看试题解析

三、解答题

15. 计算 $(\sqrt{\frac{1}{2}} + \sqrt{3}) - (\sqrt{2} - \sqrt{12})$

查看试题解析
16. 已知 $(m - 3) \sqrt{m - 2}$ ≤0，若整数k满足m+k＝ $3 \sqrt{2}$ ．试求k的值．

查看试题解析
17. 已知平行四边形ABCD中，∠A比∠B小40°，求∠C的度数．

查看试题解析
18. 如图，在平面直角坐标系中，△ABC各顶点分别是A（0，2），B（2，-2），C（4，-1）．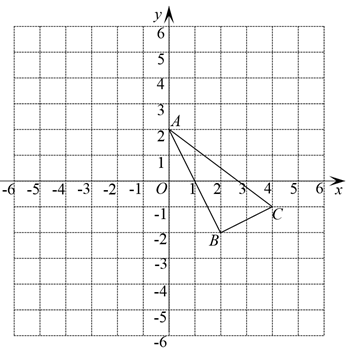

(1)、在图中作出△ABC关于y轴对称的△A₁B₁C₁；

(2)、∠ABC=°；

(3)、在第一象限内作出一点D，使 $A D = \sqrt{26}$ ，且同时 $C D = \sqrt{17}$ ．

查看试题解析
19. 如图所示，在平行四边形ABCD中，∠ABC的平分线交AD于点E，∠BCD的平分线交AD于点F，交BE于点G．

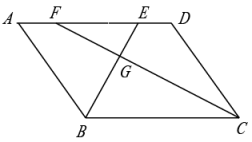(1)、若∠EFG＝32°，求∠FEG的度数；

(2)、求证：AF＝DE．

查看试题解析
20. 阅读理解
“分母有理化”是我们常用的一种化简的方法： $\frac{2 + \sqrt{3}}{2 - \sqrt{3}} = \frac{(2 + \sqrt{3}) (2 + \sqrt{3})}{(2 - \sqrt{3}) (2 + \sqrt{3})} = 7 + 4 \sqrt{3}$ ，除此之外，我们也可以用平方之后再开方的方式来化简一些有特点的无理数，如：对于 $\sqrt{3 + 5 \sqrt{5}} - \sqrt{3 - 5 \sqrt{5}}$

设 $x = \sqrt{3 + 5 \sqrt{5}} - \sqrt{3 - 5 \sqrt{5}}$ ，

易知 $\sqrt{3 + 5 \sqrt{5}} > \sqrt{3 - 5 \sqrt{5}}$

故 $x > 0$ ，由 $x^{2} = {(\sqrt{3 + 5 \sqrt{5}} - \sqrt{3 - 5 \sqrt{5}})}^{2}$

$= 3 + \sqrt{5} + 3 - \sqrt{5} - 2 \sqrt{(3 + 5 \sqrt{5}) (3 - 5 \sqrt{5})}$

$= 2$

解得 $x = \sqrt{2}$ ，即 $\sqrt{3 + 5 \sqrt{5}} - \sqrt{3 - 5 \sqrt{5}} = \sqrt{2}$ ．

根据以上方法，化简 $\frac{\sqrt{3} - \sqrt{2}}{\sqrt{3} + \sqrt{2}} + \sqrt{6 - 3 \sqrt{3}} - \sqrt{6 + 3 \sqrt{3}}$

查看试题解析
21. 如图所示，在△ABC的BC边的同侧分别作等边△ABD，等边△BCF和等边△ACE．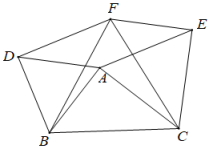

(1)、证明：△ABC≌△DBF；

(2)、证明：四边形AEFD是平行四边形；

(3)、若AB=3，AC=4，BC=5，则∠DFE的度数为°．（直接填空）

查看试题解析
22. 如图所示，在△ABC中，∠ACB＝90°，AB＝10，BC＝6，点P从点A出发，以每秒2个单位长度的速度沿折线A-B-C方向，朝着点C运动．设点P的运动时间为t秒（t＞0）．
　

(1)、在运动过程中，当t 取何值时，点P恰好在∠BAC的角平分线上；

(2)、在运动过程中，当t 取何值时，△PBC是等腰三角形．

查看试题解析
23. 如图，在平行四边形ABCD中，点O是对角线AC的中点，点E是BC上一点，且 $A B = A E$ ，连接EO并延长交AD于点F，过点B作AE的垂线，垂足为H，交AC于点G．

(1)、求证： $B E = D F$ ；

(2)、若 $∠ A C B = 4 5^{∘}$ ，解答下列问题：
①求证： $A B = B G$ ；
②当 $C G = 2$ 时，求DF的长．

查看试题解析