安徽省六安市霍邱县2021-2022学年八年级下学期期中数学试题

试卷更新日期：2023-02-28 类型：期中考试

进入出卷网下载

一、单选题

1. 下列根式中是最简二次根式的是（）

A、 $\sqrt{\frac{2}{3}}$ B、 $\sqrt{3}$ C、 $\frac{4}{\sqrt{2}}$ D、 $\sqrt{8}$

查看试题解析
2. 下列方程中，一定是一元二次方程的是（）

A、x²-2y-3＝0 B、x³-x+4＝0 C、（m+1）x²+3x+1＝0 D、2x²＝0

查看试题解析
3. 下列每一组数据中的三个数值分别为三角形的三边长，能构成直角三角形的是（）

A、 $\sqrt{3}$ ， $\sqrt{4}$ ， $\sqrt{5}$ B、4，5，6 C、6，8，10 D、 $\sqrt{5}$ ， $\sqrt{12}$ ， $\sqrt{13}$

查看试题解析
4. 用配方法解一元二次方程x²－6x＋3＝0时，配方得(　　)

A、(x＋3)²＝6 B、(x－3)²＝6 C、(x＋3)²＝3 D、(x－3)²＝3

查看试题解析
5. 关于 $x$ 的一元二次方程 $x^{2} - (2 k - 1) x + k^{2} + 1 = 0$ 有实数根，则k的取值范围是（）

A、 $k \leq - \frac{3}{4}$ B、 $k > - \frac{3}{4}$ C、 $k \geq - \frac{3}{4}$ D、 $k < - \frac{4}{3}$

查看试题解析
6. △ABC的三边长a，b，c满足 $\sqrt{a - 5}$ +（b-12）²+|c-13|＝0，则△ABC的面积是（）

A、65 B、60 C、30 D、26

查看试题解析
7. 已知 $x = 1$ 是方程 $x^{2} + a x + 2 = 0$ 的一个根，则方程的另一个根为（）

A、-2 B、2 C、-3 D、3

查看试题解析
8. 实数a、b在数轴上的位置如图所示，化简代数式 $\sqrt{{(a - b)}^{2}} + | b - \sqrt{5} | - (a + \sqrt{5})$ ，结果为（）

A、2a B、2b C、﹣2a D、2 $\sqrt{5}$

查看试题解析
9. 如图，某小区有一块长为18米，宽为6米的矩形空地，计划在其中修建两块相同的矩形绿地，它们的面积之和为60平方米，两块绿地之间及周边留有宽度相等的人行通道．若设人行道的宽度为x米，则可以列出关于x的方程是(　　)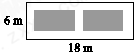

A、x²＋9x－8＝0 B、x²－9x－8＝0 C、x²－9x＋8＝0 D、2x²－9x＋8＝0

查看试题解析
10. 如图，若将上图正方形剪成四块，恰能拼成下图的矩形，设 $a = 1$ ，则 $b =$ （　　　）

A、 $\frac{\sqrt{5} - 1}{2}$ B、 $\frac{\sqrt{5} + 1}{2}$ C、 $\frac{\sqrt{5} + 3}{2}$ D、 $\sqrt{2} + 1$

查看试题解析

二、填空题

11. 若二次根式 $\sqrt{- 2 x + 4}$ 有意义，则实数x的取值范围是．

查看试题解析
12. 若m、n是一元二次方程x²﹣5x﹣2=0的两个实数根，则m+n﹣mn= ．

查看试题解析
13. 明朝数学家程大位在他的著作《算法统宗》中写了一首计算秋千绳索长度的词《西江月》：“平地秋千未起，踏板一尺离地，送行二步恰竿齐，五尺板高离地……”翻译成现代文为：如图，秋千绳索OA悬挂于O点，静止时竖直下垂，A点为踏板位置，踏板离地高度为一尺（AC＝1尺）．将它往前推进两步（EB⊥OC于点E，且EB＝10尺），踏板升高到点B位置，此时踏板离地五尺（BD＝CE＝5尺），则秋千绳索（OA或OB）长尺．

查看试题解析
14. 对于实数m，n，定义一种运算：m⊙n＝mn+n．

(1)、计算 $\sqrt{3}$ ⊙（ $\sqrt{3}$ -1）＝；

(2)、若关于x的方程x⊙（a⊙x）＝-1有两个相等的实数根，则实数a的值为．

查看试题解析

三、解答题

15. 计算：（ $\sqrt{2}$ +1）²- $\sqrt{18}$ ．

查看试题解析
16. 解方程： $x^{2} - 3 x = 1$ ．

查看试题解析
17. 若x，y为实数，且y＝ $\sqrt{x - 3}$ + $\sqrt{3 - x}$ +x+5，化简： $\sqrt{\frac{y}{x}}$ ．

查看试题解析
18. 如图，在边长为1的小正方形组成的网格中，点A，B，C都在格点上，请按要求完成下列各题．

(1)、线段AB的长为；

(2)、若三角形ABC是直角三角形，且边BC的长度为5，请在图中确定点C的位置，并补全三角形ABC．

查看试题解析
19. 已知：关于x的方程x²+2mx+m²-1=0

(1)、不解方程，判别方程根的情况；

(2)、若方程有一个根为3，求m的值．

查看试题解析
20. 有这样一道题：先化简，再求值：a+ $\sqrt{1 - 2 a + a^{2}}$ ，其中a＝1000．小亮和小芳分别给出了不同的解答过程．
小亮的解答是：原式＝a+ $\sqrt{(1 - a)^{2}}$ ＝a+1-a＝1．
小芳的解答是：原式＝a+ $\sqrt{(1 - a)^{2}}$ ＝a-（1-a）＝2a-1＝2×1000-1＝1999．

(1)、的解答是错误的；

(2)、先化简，再求值：a+2 $\sqrt{a^{2} - 6 a + 9}$ ，其中a＝-200．

查看试题解析
21. 2021年12月9日，太空课堂在中国的空间站举行，奇妙的太空试验极大地激发了青少年对探索太空的兴趣．某玩具店为满足广大青少年顾客的需求，以每个40元的进价购买了一批“天宫号空间站”的模型玩具，并以每个60元的价格出售，平均每天可售出100个．后来经过市场调查发现，单价每降低1元，则平均每天的销售量可增加10个．设每个玩具的单价降低x元．

(1)、请用含x的代数式表示：每个模型玩具的利润为元，每天可售出的模型玩具的数量为个；

(2)、若该玩具店销售这种模型玩具要想平均每天获利2240元，并尽可能让利于顾客，赢得市场，每个玩具的定价应为多少元？

查看试题解析
22. 在进行二次根式的运算时，如遇到 $\frac{1}{\sqrt{2} + 1}$ 这样的式子，我们可以按如下两种方法进行化简：
方法一： $\frac{1}{\sqrt{2} + 1} = \frac{\sqrt{2} - 1}{(\sqrt{2} + 1) \times (\sqrt{2} - 1)} = \frac{\sqrt{2} - 1}{(\sqrt{2})^{2} - 1^{2}} = \frac{\sqrt{2} - 1}{2 - 1} = \sqrt{2} - 1$ ．
方法二： $\frac{1}{\sqrt{2} + 1} = \frac{2 - 1}{\sqrt{2} + 1} = \frac{(\sqrt{2} + 1) \times (\sqrt{2} - 1)}{\sqrt{2} + 1} = \sqrt{2} - 1$ ．

(1)、请分别参照以上两种方法化简： $\frac{1}{\sqrt{5} + 2}$ ；

(2)、计算 $(\frac{1}{\sqrt{2} + 1} + \frac{1}{\sqrt{3} + \sqrt{2}} + \frac{1}{\sqrt{4} + \sqrt{3}} + ⋯ + \frac{1}{\sqrt{2022} + \sqrt{2021}}) (\sqrt{2022} + 1)$ ．

查看试题解析
23. 如图1，点C为线段BD上的一个动点，分别过点B，D作AB⊥BD，ED⊥BD，连接AC，EC．已知AB＝5，DE＝1，BD＝8，设CD＝x．

(1)、用含x的代数式表示AC+CE的长；

(2)、请在图2中画出C点位置，使AC+CE的值最小，并求出这个最小值；

(3)、根据（2）中的规律和结论，请构图求出代数式 $\sqrt{x^{2} + 4} + \sqrt{(12 - x)^{2} + 9}$ 的最小值．

查看试题解析