安徽省合肥市瑶海区2021-2022学年八年级下学期期中数学试题

试卷更新日期：2023-02-28 类型：期中考试

进入出卷网下载

一、单选题

1. 下列方程中是关于x的一元二次方程的是（）

A、 $x^{2} + \frac{1}{x} = 0$ B、ax²+bx+c＝0 C、(x﹣1)(x﹣2)＝0 D、3x²+2＝x²+2(x﹣1)²

查看试题解析
2. 下列二次根式中，最简二次根式是：（）

A、 $\sqrt{27}$ B、 $\sqrt{m^{3} n^{2}}$ C、 $\sqrt{\frac{1}{2}}$ D、 $\sqrt{6}$

查看试题解析
3. 下列各式计算正确的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $3 \sqrt{3} - 2 \sqrt{3} = 1$ C、 $2 \sqrt{3} \times \sqrt{3} = 2 \sqrt{3}$ D、 $\sqrt{6} \div \sqrt{3} = \sqrt{2}$

查看试题解析
4. 下列四组线段a、b、c，能组成直角三角形的是（　　）

A、a=4，b=5，c=6 B、a=1.5，b=2，c=2.5 C、a=2，b=3，c=4 D、a=1，b= $\sqrt{2}$ ， c=3

查看试题解析
5. 用配方法解方程x²﹣6x﹣7＝0，下列配方正确的是（　　）

A、（x﹣3）²＝16 B、（x+3）²＝16 C、（x﹣3）²＝7 D、（x﹣3）²＝2

查看试题解析
6. 若正多边形的一个外角等于45°，则这个正多边形的内角和的度数为（）

A、1080° B、1260° C、1350° D、1440°

查看试题解析
7. 如图，在矩形纸片ABCD中，AB=12，BC=5，点E在AB上，将△DAE沿DE折叠，使点A落在对角线BD上的点A′处，则AE的长为（）

A、 $\frac{10}{3}$ B、3 C、5 D、 $\frac{8}{3}$

查看试题解析
8. 已知关于x的方程 $(m - 1) x^{2} - 4 m x + 4 m - 2 = 0$ 有实数根，则m的取值范围是：（）

A、 $m \geq \frac{1}{3}$ 且 $m \neq 1$ B、 $m \geq 1$ C、 $m > \frac{1}{3}$ D、 $m \geq \frac{1}{3}$

查看试题解析
9. 如图，四边形 $A B C D$ 和四边形 $E F G H$ 均为正方形，若 $A E = a$ ， $A F = b$ ， $S_{正方形 A B C D} = S_{1}$ ， $S_{正方形 E F G H} = S_{2}$ ，则 ${(a + b)}^{2}$ 可以表示为：（）

A、 $S_{1} S_{2}$ B、 $S_{1} + S_{2}$ C、 $2 S_{1} - S_{2}$ D、 $2 S_{2} S_{1}$

查看试题解析
10. 对于一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ ，下列说法：
①若 $a - b + c = 0$ ，则 $b^{2} - 4 a c \geq 0$ ；
②若方程 $a x^{2} + c = 0$ 有两个不相等的实根，则方程 $a x^{2} + b x + c = 0$ 必有两个不相等的实根；
③若 $c$ 是方程 $a x^{2} + b x + c = 0$ 的一个根，则一定有 $a c + b + 1 = 0$ 成立；
④若 $x_{0}$ 是一元二次方程 $a x^{2} + b x + c = 0$ 的根，则 $b^{2} - 4 a c = {(2 a x_{0} + b)}^{2}$
其中正确的：（）

A、只有① B、只有①② C、①②③ D、只有①②④

查看试题解析

二、填空题

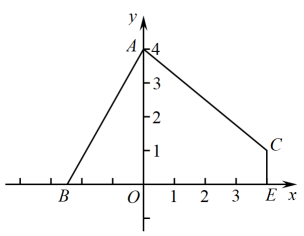
11. 过十边形的一个顶点，可以引出对角线的条数为．

查看试题解析
12. 参加一次同学聚会，每两人都握一次手，所有人共握了15次，若设共有x人参加同学聚会．列方程得．

查看试题解析
13. 已知关于x的一元二次方程 $x^{2} + m x + n = 0$ 的一个解是 $x = 2$ ，另一个解是正数，而且也是方程 ${(x + 4)}^{2} - 22 = 9 x$ 的解，则m+n= ．

查看试题解析
14. 如图，点B为x轴上的一个动点，点A的坐标为 $(0 ， 4)$ ，点C的坐标为 $(4 ， 1)$ ， $C E ⊥ x$ 轴于E点，当点B的坐标为时， $△ A B C$ 为直角三角形．

查看试题解析

三、解答题

15. 计算： $\sqrt{\frac{1}{3}} + \sqrt{6} \times (\frac{1}{\sqrt{2}} + \sqrt{8}) - | \sqrt{3} - 2 |$ ．

查看试题解析
16. 解方程

(1)、 $x (x - 3) = x - 3$ ．

(2)、 $x^{2} - 6 x + 8 = 0$ ．

查看试题解析
17. 已知：a= $\sqrt{5}$ +2，b= $\sqrt{5}$ －2．

(1)、求ab．

(2)、求 $a^{2} + b^{2} - a b$

查看试题解析
18. 探究：已知，如图是一个三角形点阵，从上向下数有无数多行，其中第一行有一个点，第二行有两个点，…，第n行有n个点…，容易发现，10是三角形点阵中前4行的点数和．

(1)、求三角形点阵中前10行的点数和；

(2)、若三角形点阵中前a行的点数之和为300，求a的值；

(3)、三角形点阵中前b行的点数之和能是600吗？（填“能”或“不能”）

查看试题解析
19. 如图正方形网格中，每个小正方形的边长均为1，在如图的网格格点处取A，B，C三点，使AB＝2 $\sqrt{2}$ ， BC＝ $\sqrt{10}$ ， AC＝ $\sqrt{26}$ ．

(1)、请你在图中画出满足条件的△ABC；

(2)、求△ABC的面积；

(3)、直接写出点A到线段BC的距离．

查看试题解析
20. 我国在扶贫方面取得了巨大的成就，技术扶贫也使得某县的一个电子器件厂扭亏为盈．该电子器件厂生产一种电脑声卡，2020年该类电脑声卡的成本是200元/个，2021年与2022年连续两年在技术扶贫的帮助下改进技术，降低成本，2022年该电脑声卡的成本降低到162元/个．

(1)、若这两年此类电脑声卡成本下降的百分率相同，求平均每年下降的百分率；

(2)、2022年某商场以高于成本价10%的价格购进若干个此类电脑声卡，以216.2元/个销售时，平均每天可销售20个，为了减少库存，商场决定降价销售，经调查发现，单价每降低5元，每天可多售出10个，如果每天盈利1120元，单价应降低多少元？

查看试题解析
21. 小芳在解决问题：已知a＝ $\frac{1}{2 + \sqrt{3}}$ ，求2a²﹣8a+1的值.他是这样分析与解的：
a＝ $\frac{1}{2 + \sqrt{3}}$ ＝ $\frac{2 - \sqrt{3}}{(2 + \sqrt{3}) (2 - \sqrt{3})}$ ＝2﹣ $\sqrt{3}$ ，
∴a＝2﹣ $\sqrt{3}$ ，
∴(a﹣2)²＝3，a²﹣4a+4＝3，
∴a²﹣4a＝﹣1，
∴2a²﹣8a+1＝2(a²﹣4a)+1＝2×(﹣1)+1＝﹣1
请你根据小芳的分析过程，解决如下问题：

(1)、计算： $\frac{1}{\sqrt{2} + 1} + \frac{1}{\sqrt{3} + \sqrt{2}} + \frac{1}{\sqrt{4} + \sqrt{3}} + \dots + \frac{1}{\sqrt{2022} + \sqrt{2021}}$ .

(2)、若 $a = \frac{1}{\sqrt{2} - 1}$ .
①求4a²﹣8a﹣1的值；
②求3a³﹣12a²+9a﹣12的值.

查看试题解析
22. 阅读材料：我们已经学习了《二次根式》和《乘法公式》，可以发现：当 $a > 0$ ， $b > 0$ 时，有 $(\sqrt{a} - \sqrt{b})^{2} = a - \sqrt{a b} + b \geq 0$ ， ∴ $a + b \geq 2 \sqrt{a b}$ ，当且仅当 $a = b$ 时取等号．即 $a + b$ 有最小值 $2 \sqrt{a b}$ ．
请利用上述结论解决以下问题：

(1)、①当 $x > 0$ 时， $x + \frac{1}{x}$ 的最小值为；②当 $x < 0$ 时， $x + \frac{1}{x}$ 的最大值为．

(2)、①当 $x > 0$ 时，求 $\frac{x^{2} + 3 x + 25}{x}$ 的最小值；②若 $a > 1$ ，求 $a + \frac{25}{a - 1}$ 的最小值．

查看试题解析
23.

(1)、观察猜想
如图①点B、A、C在同一条直线上，DB⊥BC，EC⊥BC且∠DAE=90°，AD=AE，则BC、BD、CE之间的数量关系为；

(2)、问题解决
如图②，在Rt△ABC中，∠ABC=90°，CB=4，AB=2，以AC为直角边向外作等腰Rt△DAC，连结BD，求BD的长；

(3)、拓展延伸
如图③，在四边形ABCD中，∠ABC=∠ADC=90°，CB=4，AB=2，DC=DA，请直接写出BD的长.

查看试题解析