安徽省合肥市庐江县2021-2022学年八年级下学期期中数学试题

试卷更新日期：2023-02-28 类型：期中考试

进入出卷网下载

一、单选题

1. 下列二次根式中是最简二次根式的是（）

A、 $\sqrt{\frac{1}{2}}$ B、 $\sqrt{6}$ C、 $\sqrt{8}$ D、 $\sqrt{9}$

查看试题解析
2. 如图，直线 $a ∥ b$ ，则直线 $a ， b$ 之间的距离是（）

A、线段 $A B$ B、线段 $A B$ 的长度 C、线段 $C D$ D、线段 $C D$ 的长度

查看试题解析
3. $R t △ A B C$ 的斜边为13，其中一条直角边为12，另一条直角边的长为（）

A、5 B、6 C、7 D、9

查看试题解析
4. 当 $x > 2$ 时， $\sqrt{{(2 - x)}^{2}}$ = （）

A、 $2 - x$ B、 $x - 2$ C、 $2 + x$ D、 $\pm (x - 2)$

查看试题解析
5. 若3、4、a为勾股数，则a的值为（）

A、 $\sqrt{7}$ B、5 C、5或7 D、5或 $\sqrt{7}$

查看试题解析
6. 下列计算正确的是（）

A、 $\sqrt{7} - \sqrt{3} = 2$ B、 $\sqrt{2} \times \sqrt{5} = \sqrt{7}$ C、 $2 \div \sqrt{2} = \sqrt{2}$ D、 $\sqrt{7} + \sqrt{7} = \sqrt{14}$

查看试题解析
7. 如图，在 $△ A B C$ 中， $A B = C B = 6$ ， $B D ⊥ A C$ 于点D，F在BC上且 $B F = 2$ ，连接AF，E为AF的中点，连接DE，则DE的长为（）

A、1 B、2 C、3 D、4

查看试题解析
8. 如图，菱形ABCD中，AC＝6，BD＝8，AH⊥BC于点H．则AH＝（　　）

A、24 B、10 C、 $\frac{24}{5}$ D、 $\frac{12}{5}$

查看试题解析
9. 如图，高速公路的同一侧有A，B两城镇，它们到高速公路所在直线 $M N$ 的距离分别为 $A C = 2 k m$ ， $B D = 4 k m$ ，且 $C D = 8 k m$ ，要在高速公路上C，D之间建一个出口P，使A，B两城镇到P的距离之和最小，则这个最短距离为（）

A、 $8 k m$ B、 $10 k m$ C、 $12 k m$ D、 $10 \sqrt{2} k m$

查看试题解析
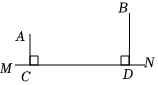10. 如图，矩形ABCD中，AB=12，点E是AD上的一点，AE=6，BE的垂直平分线交BC的延长线于点F ，连接EF交CD于点G ，若G是CD的中点，则BC的长是（）

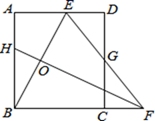A、12.5 B、12 C、10 D、10.5

查看试题解析

二、填空题

11. 若式子 $\sqrt{3 x - 6}$ 有意义，则x的取值范围是．

查看试题解析
12. 如图，在平面直角坐标系中，以O为圆心，以OP的长为半径画弧，交x轴的负半轴于点A，则点A的坐标为（- $\sqrt{17}$ ， 0），点P的纵坐标为-1，则P点的坐标为．

查看试题解析
13. 如图，在 $R t △ A B C$ 中， $∠ A B C = 90 °$ ， $B D ⊥ A C$ 于点D， $∠ A B D = 3 ∠ C B D$ ， E是斜边 $A C$ 的中点， $∠ E B D$ 的度数是°．

查看试题解析
14. 如图，已知正方形 $A B C D$ 的边长为 $6 c m$ ， E为边 $A B$ 上一点，且 $A E$ 长为 $1 c m$ ，动点P从点B出发以每秒 $1 c m$ 的速度沿射线 $B C$ 方向运动．把 $△ E B P$ 沿 $E P$ 折叠，点B落在点 $B^{'}$ 处，设运动时间为t秒．

(1)、当 $t =$ 时， $∠ B^{'} P C$ 为直角；

(2)、若点 $B^{'}$ 到直线 $A D$ 的距离为 $3 c m$ ，则 $B P$ 长为．

查看试题解析

三、解答题

15. 计算： ${(\sqrt{3} + 1)}^{2} - (3 \sqrt{2} - \sqrt{6}) \div \sqrt{6}$ ．

查看试题解析
16. 如图，在 $▱ A B C D$ 中，对角线 $A C$ 和 $B D$ 相交于点O， $B D ⊥ A D$ ， $A B = 10$ ， $A D = 8$ ，求 $O B$ 的长．

查看试题解析
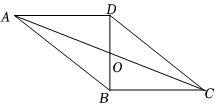17. 将两个全等的直角三角形按如图所示摆放，使点A、E、D在同一条直线上．利用此图的面积表示式证明勾股定理．

查看试题解析
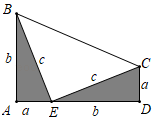18. 观察下列等式：
第1个等式： $\sqrt{1 \times 5 + 4} = 3$ ；
第2个等式： $\sqrt{2 \times 6 + 4} = 4$ ；
第3个等式： $\sqrt{3 \times 7 + 4} = 5$ ；
第4个等式： $\sqrt{4 \times 8 + 4} = 6$ ；
……
按照以上规律，解决下列问题：

(1)、填空：＝10；

(2)、填空：＝n（ $n \geq 3$ 且n为正整数），并证明这个等式．

查看试题解析
19. 如图，网格中每个小正方形的边长都是1．

(1)、线段 $A B$ 的长度是；

(2)、请在网格中画出线段 $A C = \sqrt{5}$ ， $B D = 2 \sqrt{2}$ ，且C，D为 $A B$ 右侧的格点（网格线的交点）；

(3)、以 $A B$ 、 $A C$ 、 $B D$ 三条线段为边能否构成直角三角形，并说明理由．

查看试题解析
20. 如图， $△ A B C$ 中， $D ， E$ 分别是 $A C ， A B$ 的中点， $D E = \frac{1}{2} C E$ ，过点B作 $B F ∥ C E$ ，交 $D E$ 的延长线于点F.

(1)、求证：四边形 $B C E F$ 是菱形.

(2)、若 $B C = 6 ， ∠ B C E = 60 °$ ，求菱形 $B C E F$ 的面积.

查看试题解析
21. 为推进乡村振兴，把家乡建设成为生态宜居、交通便利的美丽家园，某地大力修建崭新的公路．如图所示，现从A地分别向C、D、B三地修了三条笔直的公路 $A C$ 、 $A D$ 和 $A B$ ， C地、D地、B地在同一笔直公路上，公路 $A C$ 和公路 $C B$ 互相垂直，又从D地修了一条笔直的公路 $D H$ 与公路 $A B$ 在H处连接，且公路 $D H$ 和公路 $A B$ 互相垂直，已知 $A C = 9$ 千米， $A B = 15$ 千米，
$B D = 5$ 千米．

(1)、求公路 $C D$ 的长度；

(2)、若修公路 $D H$ 每千米的费用是2000万元，请求出修建公路 $D H$ 的总费用．

查看试题解析
22. 我们规定用 $(a ， b)$ 表示-对数对，给出如下定义：记 $m = \frac{1}{\sqrt{a}}$ ， $n = \sqrt{b}$ （ $a > 0$ ， $b > 0$ ），将 $(m ， n)$ 与 $(n ， m)$ 称为数对 $(a ， b)$ 的一对“对称数对”，例如： $(4 ， 1)$ 的一对“对称数对”为 $(\frac{1}{2} ， 1)$ 与 $(1 ， \frac{1}{2})$ ．

(1)、数对 $(25 ， 4)$ 的一对“对称数对”是和；

(2)、若数对 $(x ， 2)$ 的一对“对称数对”的一个数对是 $(\sqrt{2} ， 1)$ ，求x的值；

(3)、若数对 $(a ， b)$ 的一对“对称数对”的一个数对是 $(\sqrt{3} ， 3 \sqrt{3})$ ，求 $a b$ 的值．

查看试题解析
23. 如图，把一个等腰直角三角板 $A E M$ 放置于矩形 $A B C D$ 上， $A E = B C = 13$ ， $A B = 24$ ．三角板的一个锐角的顶点放在A处，且直角边 $A E$ 在矩形内部绕点A旋转，在旋转过程中 $E M$ 与 $C D$ 交于点F．

(1)、如下图，
①旋转过程中线段 $D F$ 与 $E F$ 有何数量关系？并给出证明；
②连接 $E C$ ， $E B$ ，若 $△ E C B$ 为等腰三角形，求 $D F$ 的长；

(2)、如下图，以 $A D$ 为边在矩形内部作正方形 $A D H I$ ，直角边 $E M$ 所在的直线交 $H I$ 于O，交 $A B$ 于G，设 $D F = m$ ，请你用m的代数式表示 $O H$ 的长．

查看试题解析