2022-2023浙教版数学八年级下册 第三章 数据分析初步 单元复习

试卷更新日期：2023-02-28 类型：单元试卷

进入 出卷网 下载

一、单选题（每题4分，共40分）

  • 1. 下列几个常见统计量中能够反映一组数据变化范围大小的是（   ）
    A、方差 B、中位数 C、众数 D、极差

    查看试题解析

  • 2. 一组数据分别为3、5、8、4、7，这组数据的中位数为（  ）
    A、4 B、5 C、7 D、8

    查看试题解析

  • 3. 已知一组数据2，2，5，x，5，3有唯一的众数5，则x的值是（   ）
    A、3 B、5 C、2 D、无法确定

    查看试题解析

  • 4. 某校在“科技创新”比赛中，对甲、乙、丙三项作品进行量化评分（百分制），如表：如果按照创新性占60%，实用性占40%计算总成绩，并根据总成绩择优推荐，那么应推荐的作品是（   ）

    项目作品

    甲

    乙

    丙

    创新性

    90

    95

    90

    实用性

    90

    90

    95

    A、甲 B、乙 C、丙 D、甲和丙

    查看试题解析

  • 5. 甲、乙、丙、丁四位同学都参加了5次数学模拟测试，每个人这5次成绩的平均数都是125分，方差分别是S甲 2=0.65 ， S乙 2=0.55 ， S丙 2=0.50 ， S丁2=0.45 ， 则这5次测试成绩最稳定的是（       ）
    A、甲 B、乙 C、丙 D、丁

    查看试题解析

  • 6. 某同学对数据35，29，32，32，4■，45，45进行统计分析，发现两位数“4■”的个位数字模糊不清，则下列统计量一定不受影响的是（   ）
    A、平均数 B、中位数 C、众数 D、方差

    查看试题解析

  • 7. 若x1 ， x2 ， x3 ， ⋯，xn的平均数为8，方差为2，则关于x1＋2，x2＋2，x3＋2，……，xn＋2，下列结论正确的是（  ）
    A、平均数为8，方差为2 B、平均数为8，方差为4 C、平均数为10，方差为2 D、平均数为10，方差为4

    查看试题解析

  • 8. 为了从四名同学中选出一人参加计算机编程比赛，对他们进行了多次测试，并对每个人的测试成绩的平均数及方差进行了统计（如下表），则应选的同学是（  ）

    学生

    学生一

    学生二

    学生三

    学生四

    平均数

    95

    96

    96

    95

    方差

    5

    5

    4.8

    4.8

    A、学生一 B、学生二 C、学生三 D、学生四

    查看试题解析

  • 9. 跳远运动员李强在一次训练中，先跳了6次的成绩如下：7.6，7.8，7.7，7.8，8.0，7.9（单位：m）．这六次成绩的平均数为7.8，方差为160 ． 如果李强再跳两次，成绩分别为7.6，8.0，则李强这8次跳远成绩与前6次的成绩相比较，其方差 （  ）．
    A、变大 B、变小 C、不变 D、无法确定

    查看试题解析

  • 10.

    在某次训练中，甲、乙两名射击运动员各射击10发子弹的成绩统计图如图所示，对于本次训练，有如下结论：①S甲2＞S乙2；②S甲2＜S乙2；③甲的射击成绩比乙稳定；④乙的射击成绩比甲稳定，由统计图可知正确的结论是（　　）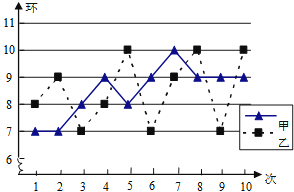

    A、①③ B、①④ C、②③ D、②④

    查看试题解析

二、填空题（每空5分，共30分）

  • 11. 在东京奥运会比赛前，有甲、乙、丙、丁四位选手各10次射击成绩的平均数和方差如下表，则这四人成绩最好且发挥最稳定的是 ．

    选手

    甲

    乙

    丙

    丁

    平均数（环）

    9.4

    9.4

    9.2

    9.2

    方差（环2）

    0.035

    0.015

    0.025

    0.027

    查看试题解析

  • 12. 某校八年级有7名同学的体能测试成绩（单位：分）如下：50，48，47，50，48，49，48.这组数据的众数是分．

    查看试题解析

  • 13. 在本学期的五次数学检测中，甲同学的成绩如下：92，89，88，87，94，乙同学的成绩如下：78，88，98，94，98，两名同学成绩比较稳定的是 （“甲”或“乙”）．

    查看试题解析

  • 14. 某校规定学生期末数学总评成绩由三部分构成：卷面成绩、课外论文成绩、平日表现成绩（三部分所占比例如图），若方方的三部分得分依次是92、80、84，则她这学期的期末数学总评成绩是 ．

    查看试题解析

  • 15. 为迎接体育测试，小强每天坚持引体向上锻炼，他记录了某一周每天做引体向上的个数，如下表：

    其中有三天的个数被墨汁覆盖了，但小强已经计算出这组数据唯一的众数是13，平均数是12，那么这组数据的方差是。

    查看试题解析

  • 16. 某学校九（1）班40名同学的期中测试成绩分别为 a1 ， a2 ， a3 ，……， a40 .已知 a1 + a2 + a3 +……+ a40 = 4800，y= (a−a1)2 + (a−a2)2 + (a−a2)2 +……+ (a−a40)2 ，当y取最小值时， 的值为.

    查看试题解析

三、解答题（共6题，共80分）

  • 17.

    为迎接中国共产党建党90周年，某校举办“红歌伴我成长”歌咏比赛活动，参赛同学的成绩分别绘制成频数分布表和频数分布直方图（均不完整）如下：

    分数段

    频数

    频率

    80≤x＜85

    9

    0.15

    85≤x＜90

    m

    0.45

    90≤x＜95

    ■

    ■

    95≤x＜100

    6

    n

    （1）求m，n的值分别是多少；

    （2）请在图中补全频数分布直方图；

    （3）比赛成绩的中位数落在哪个分数段？

    查看试题解析

  • 18. 某养鱼个体经营户在鱼塘放养了5500条草鱼苗，鱼苗的成活率为90%．养殖一段时间后，想估计鱼塘中产量，随机网了三次，第一次网出30条鱼，平均每条鱼的重量是1kg；第二次网出了45条鱼，平均每条鱼的重量是1.3kg；第三次网出了35条鱼，平均每条鱼的重量是1.2kg，请你估计鱼塘中鱼的总重量是多少kg？

    查看试题解析

  • 19. 端午假期刚过，集美龙舟队有开始新的一轮训练，为更加有效训练队员，集美龙舟队决定公开招聘教练，经过笔试后筛选出甲、乙两位教练进行面试和体侧，两人的成绩如右表．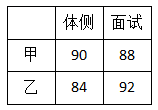

    (1)、当体侧成绩权重为6，面试成绩权重为4，请问甲、乙两人谁的成绩高？
    (2)、当体侧成绩权重为 a ，面试和体侧各有权重，并且权总和为10，请问当 a 取什么范围，乙成绩比甲高？

    查看试题解析

  • 20. 电影《长津湖》和《水门桥》是两部聚焦抗美援朝历史的影片，从观看过这两部电影的学生中各随机抽取了20名学生进行调查，让他们给这两部电影评分，下列图表是调查中的部分信息．

    根据以上信息，解答下列问题：

    (1)、电影《长津湖》得分的中位数和众数分别是多少？
    (2)、电影《水门桥》得分的平均数是多少？
    (3)、若该校有200名学生观看过这两部影片，且他们都对这两部作品进行评分，你认为这两部作品一共可以得到多少个满分？

    查看试题解析

  • 21. 本学期开学初，学校体育组对九年级某班50名学生进行了跳绳项目的测试，根据测试成绩制作了下面两个统计图．

    根据统计图解答下列问题：

    (1)、本次测试的学生中，得4分的学生有多少人？
    (2)、本次测试的平均分是多少分？
    (3)、通过一段时间的训练，体育组对该班学生的跳绳项目进行第二次测试，测得成绩的最低分为3分，且得4分和5分的人数共有45人，平均分比第一次提高了0.8分，问第二次测试中得4分、5分的学生各有多少人？

    查看试题解析

  • 22. 为提高节水意识，小申随机统计了自己家7天的用水量，并分析了第3天的用水情况，将得到的数据进行整理后，绘制成如图所示的统计图.（单位：升）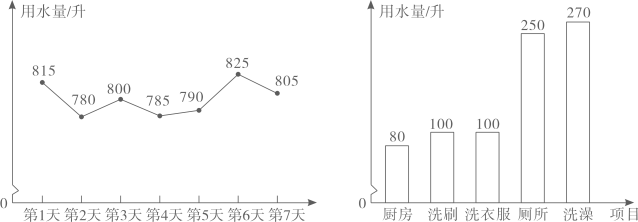

    (1)、求这7天内小申家每天用水量的平均数和中位数；
    (2)、求第3天小申家洗衣服的水占这一天总用水量的百分比；
    (3)、请你根据统计图中的信息，给小申家提出一条合理的节约用水建议，并估算采用你的建议后小申家一个月（按30天计算）节约的用水量。

    查看试题解析