2022-2023浙教版数学八年级下册第二章一元一次方程单元复习

试卷更新日期：2023-02-28 类型：单元试卷

进入出卷网下载

一、单选题（每题4分，共40分）

1. 下列方程是关于x的一元二次方程的是（）

A、 $x^{2} + \frac{1}{x} = 1$ B、 $a x^{2} + b x + c = 0$ C、 $(x + 1) (x + 2) = 1$ D、 $(x - 3)^{2} + 4 = x^{2}$

查看试题解析
2. 一元二次方程x（x-2）=0的解是（）

A、x=2 B、x=0 C、x₁=0，x₂=2 D、x₁=0，x₂=-2

查看试题解析
3. 某电影上映第一天票房收入约1亿元，以后每天票房收入按相同的增长率增长，三天后累计票房收入达到4亿元.若增长率为 $x$ ，则下列方程正确的是（）

A、 $1 + x = 4$ B、 ${(1 + x)}^{2} = 4$ C、 $1 + {(1 + x)}^{2} = 4$ D、 $1 + (1 + x) + {(1 + x)}^{2} = 4$

查看试题解析
4. 方程 $2 x^{2} = 3 (x - 6)$ 化为一般形式后二次项系数、一次项系数、常数项分别是（）

A、2，3，-6 B、2，-3，18 C、2，-3，6 D、2，3，6

查看试题解析
5. 已知 $x_{1} ， x_{2}$ 是一元二次方程 $x^{2} + 2 a x + b = 0$ 的两个根，且 $x_{1} + x_{2} = 3 ， x_{1} \cdot x_{2} = 1$ ，则a，b的值分别是（）

A、 $a = - 3 ， b = 1$ B、 $a = 3 ， b = 1$ C、 $a = - \frac{3}{2} ， b = - 1$ D、 $a = - \frac{3}{2} ， b = 1$

查看试题解析
6. 以 $x = \frac{4 \pm \sqrt{16 + 4 c}}{2}$ 为根的一元二次方程可能是（）

A、 $x^{2} - 4 x - c = 0$ B、 $x^{2} + 4 x - c = 0$ C、 $x^{2} - 4 x + c = 0$ D、 $x^{2} + 4 x + c = 0$

查看试题解析
7. 电影《长津湖》讲述了一段波澜壮阔的历史，自上映以来，全国票房连创佳绩．据不完全统计，某市第一天票房收入约 $2$ 亿元，第三天票房收入约达到 $4$ 亿元，设票房收入每天平均增长率为 $x$ ，下面所列方程正确的是（）

A、 $2 (1 + x)^{2} = 4$ B、 $2 (1 + 2 x) = 4$ C、 $2 (1 - x)^{2} = 4$ D、 $2 + 2 (1 + x) + 2 (1 + x)^{2} = 4$

查看试题解析
8. 关于x的一元二次方程x²＋kx－1=0的根的情况是（）

A、有两个不相等的同号实数根 B、有两个不相等的异号实数根 C、有两个相等的实数根 D、没有实数根

查看试题解析
9. 如图，将图1的正方形剪成四块，恰能拼成图2的矩形，则 $\frac{b}{a} =$ （）

A、 $\frac{\sqrt{5} - 1}{2}$ B、 $\frac{\sqrt{5} + 3}{2}$ C、 $\frac{\sqrt{5} + 1}{2}$ D、 $\sqrt{2} + 1$

查看试题解析
10. 一元二次方程 $M ： a x^{2} + b x + c = 0 ； N ： c x^{2} + b x + a = 0$ ，其中 $a c \neq 0 ， a \neq c$ ，给出以下四个结论：(1)若方程 $M$ 有两个不相等的实数根，则方程 $N$ 也有两个不相等的实数根；(2)若方程 $M$ 的两根符号相同，则方程 $N$ 的两根符号也相同；(3)若 $m$ 是方程 $M$ 的一个根，则 $\frac{1}{m}$ 是方程 $N$ 的一个根；(4)若方程 $M$ 和方程 $N$ 有一个相同的根，则这个根必是 $x = 1$ .其中正确的个数是（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题（每空5分，共30分）

11. 关于x的方程 $x^{2} + m x = 0$ 的一个根是-2，则m的值为．

查看试题解析
12. 代数式 $x^{2} - 2 x$ 与4x的值相等，则x的值为．

查看试题解析
13. 为响应“把中国人的饭碗牢牢端在自己手中”的号召，确保粮食安全，优选品种，提高产量，某农业科技小组对原有的小麦品种进行改良种植研究．在保持去年种植面积不变的情况下，今年预计小麦平均亩产量将在去年的基础上增加a%，因为优化了品种，预计每千克售价将在去年的基础上上涨2a%，全部售出后预计总收入将增加68%，则a的值为．

查看试题解析
14. 对于实数 $m$ ， $n$ ，定义一种运算 $*$ 为： $m * n = m n + n .$ 如果关于 $x$ 的方程 $x * (a * x) = - \frac{1}{4}$ 有两个相等的实数根，则 $a =$ .

查看试题解析
15. 如果关于x的一元二次方程ax²+bx+c＝0有两个实数根，且其中一个根为另一个根的2倍，则称这样的方程为“倍根方程”，若（x﹣1）（mx﹣n）＝0是倍根方程，则 $\frac{2 n}{m}$ 的值为.

查看试题解析
16. 在△ABC中，已知两边a=3，b=4，第三边为c．若关于x的方程 $x^{2} + (c - 4) x + \frac{1}{4} = 0$ 有两个相等的实数根，则该三角形的面积是

查看试题解析

三、计算题（共2题，共18分）

17. 解方程： $x^{2} - 4 = 3 (x - 2)$

查看试题解析
18. 按要求解下列方程：

(1)、（2x﹣3）²+x（2x﹣3）＝0（因式分解法）；

(2)、2x²﹣4x﹣1＝0（用配方法）．

查看试题解析

四、解答题（共6题，共62分）

19. 已知关于x的一元二次方程x²−mx+m−2=0．

(1)、求证：此方程总有两个不相等的实数根；

(2)、若此方程有一个根是0，求出m的值和另一个根．

查看试题解析
20. “双减”政策倡导学生合理使用电子产品，控制使用时长，防止网络沉迷．某品牌学习机商店，为了提高学习机的销量，减少库存，决定对该品牌学习机进行降价销售，经市场调查，当学习机的售价为每台1800元时，每天可售出4台，在此基础上，售价每降低50元，每天将多售出1台．已知每台学习机的进价为1000元．如果该品牌学习机商店拟获利4200元，该商店需要将每台学习机售价定为多少元？

查看试题解析
21. 对于竖直向上抛出的物体，在不考虑空气阻力的情况下，有如下的关系式：h=vt- $\frac{1}{2}$ gt² ，其中h是物体上升的高度，v是抛出时的速度，g是重力加速度（g≈10m/s²），t是抛出后的时间.如果一物体以25m/s的初速度从地面竖直向上抛出，经过几秒钟后它在离地面20m高的地方？

查看试题解析
22. 某小区计划用40米的篱笆围一个矩形花坛，其中一边靠墙 $($ 墙足够长，篱笆要全部用完 $)$ .

(1)、如图1，问 $AB$ 为多少米时，矩形 $ABCD$ 的面积为200平方米？

(2)、如图2，矩形 $EMNF$ 的面积比（1）中的矩形 $ABCD$ 面积减小20平方米，小明认为只要此时矩形的长 $MN$ 比图①中矩形的长 $BC$ 少2米就可以了.请你通过计算，判断小明的想法是否正确.

查看试题解析
23. 如图，在直角梯形 $A B C D$ 中， $A D ∥ B C$ ， $∠ C = 90 °$ ， $B C = 16$ ， $D C = 12$ ， $A D = 21$ ．动点 $P$ 从点 $D$ 出发，沿射线 $D A$ 的方向以每秒2个单位的速度运动，动点 $Q$ 从点 $C$ 出发，沿射线 $C B$ 的方向以每秒1个单位的速度向点 $B$ 运动，点 $P$ ， $Q$ 分别从点 $D$ ， $C$ 同时出发，当点 $P$ 运动到点 $A$ 时，点 $Q$ 随之停止运动．设运动的时间为 $t$ （秒），当 $t$ 为何值时，以 $B$ ， $P$ ， $Q$ 三点为顶点的三角形是等腰三角形？

查看试题解析
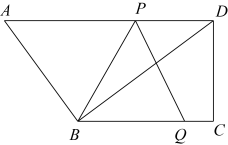24. 综合与探究：如果关于x的一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ 有两个实数根，且其中一个根比另一个根大1，那么称这样的方程是“邻根方程”．例如：一元二次方程 $x^{2} + x = 0$ 的两个根是 $x_{1} = 0$ ， $x_{2} = - 1$ ，则方程： $x^{2} + x = 0$ 是“邻根方程”．

(1)、通过计算，判断下列方程是否是“邻根方程”：
① $x^{2} + x - 6 = 0$ ；② $2 x^{2} - 2 \sqrt{5} x + 2 = 0$ ．

(2)、已知关于x的一元二次方程 $x^{2} - (m - 2) x - 2 m = 0$ （m是常数）是“邻根方程”，求m的值．

查看试题解析

2022-2023浙教版数学八年级下册 第二章 一元一次方程 单元复习

一、单选题（每题4分，共40分）

二、填空题（每空5分，共30分）

三、计算题（共2题，共18分）

四、解答题（共6题，共62分）

2022-2023浙教版数学八年级下册第二章一元一次方程单元复习