2023年中考数学精选真题实战测试54 直线与圆的位置关系 B
试卷更新日期:2023-02-26 类型:二轮复习
一、单选题(每题3分,共30分)
-
1. 如图,是的直径,点P在的延长线上,与相切于点A,连接 , 若 , 则的度数为( )
 A、 B、 C、 D、2. 工人师傅为检测该厂生产的一种铁球的大小是否符合要求,设计了一个如图(1)所示的工件槽,其两个底角均为90°,将形状规则的铁球放入槽内时,若同时具有图(1)所示的A、B、E三个接触点,该球的大小就符合要求.图(2)是过球心及A、B、E三点的截面示意图,已知⊙O的直径就是铁球的直径,AB是⊙O的弦,CD切⊙O于点E,AC⊥CD、BD⊥CD,若CD=16cm,AC=BD=4cm,则这种铁球的直径为( )
A、 B、 C、 D、2. 工人师傅为检测该厂生产的一种铁球的大小是否符合要求,设计了一个如图(1)所示的工件槽,其两个底角均为90°,将形状规则的铁球放入槽内时,若同时具有图(1)所示的A、B、E三个接触点,该球的大小就符合要求.图(2)是过球心及A、B、E三点的截面示意图,已知⊙O的直径就是铁球的直径,AB是⊙O的弦,CD切⊙O于点E,AC⊥CD、BD⊥CD,若CD=16cm,AC=BD=4cm,则这种铁球的直径为( ) A、10cm B、15cm C、20cm D、24cm3. 如图,在四边形材料中, , , , , .现用此材料截出一个面积最大的圆形模板,则此圆的半径是( )
A、10cm B、15cm C、20cm D、24cm3. 如图,在四边形材料中, , , , , .现用此材料截出一个面积最大的圆形模板,则此圆的半径是( )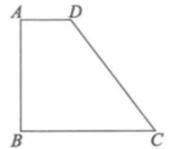 A、 B、8cm C、 D、10cm4. 如图是不倒翁的主视图,不倒翁的圆形脸恰好与帽子边沿PA,PB分别相切于点A,B,不倒翁的鼻尖正好是圆心O,若∠OAB=28°,则∠APB的度数为( )
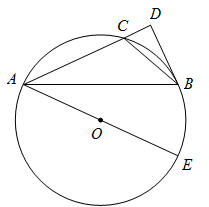
A、 B、8cm C、 D、10cm4. 如图是不倒翁的主视图,不倒翁的圆形脸恰好与帽子边沿PA,PB分别相切于点A,B,不倒翁的鼻尖正好是圆心O,若∠OAB=28°,则∠APB的度数为( ) A、 B、 C、 D、5. 为⊙ 外一点, 与⊙ 相切于点 , , ,则 的长为( )A、 B、5 C、8 D、96. 已知平面内有⊙O和点A , B , 若⊙O半径为2cm , 线段OA=3cm , OB=2cm , 则直线AB与⊙O的位置关系为( )A、相离 B、相交 C、相切 D、相交或相切7. 如图, 是 的弦,点 在过点 的切线上, , 交 于点 .若 ,则 的度数等于( )
A、 B、 C、 D、5. 为⊙ 外一点, 与⊙ 相切于点 , , ,则 的长为( )A、 B、5 C、8 D、96. 已知平面内有⊙O和点A , B , 若⊙O半径为2cm , 线段OA=3cm , OB=2cm , 则直线AB与⊙O的位置关系为( )A、相离 B、相交 C、相切 D、相交或相切7. 如图, 是 的弦,点 在过点 的切线上, , 交 于点 .若 ,则 的度数等于( )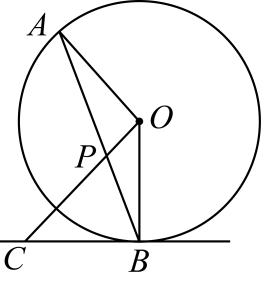 A、 B、 C、 D、8. 如图, 为 的直径,点P在 的延长线上, 与 相切,切点分别为C,D.若 ,则 等于( )
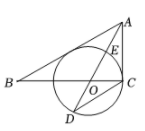
A、 B、 C、 D、8. 如图, 为 的直径,点P在 的延长线上, 与 相切,切点分别为C,D.若 ,则 等于( )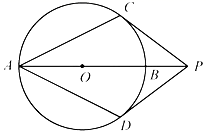 A、 B、 C、 D、9. 如图, 、 分别与 相切于 、 , , 为 上一点,则 的度数为( )
A、 B、 C、 D、9. 如图, 、 分别与 相切于 、 , , 为 上一点,则 的度数为( )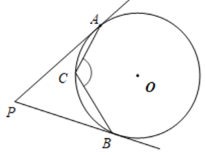 A、 B、 C、 D、10. 如图,∠BAC=36°,点O在边AB上,⊙O与边AC相切于点D,交边AB于点E,F,连接FD,则∠AFD等于( )
A、 B、 C、 D、10. 如图,∠BAC=36°,点O在边AB上,⊙O与边AC相切于点D,交边AB于点E,F,连接FD,则∠AFD等于( )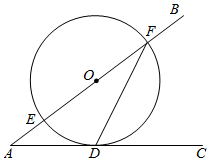 A、27° B、29° C、35° D、37°
A、27° B、29° C、35° D、37°二、填空题(每空3分,共18分)
-
11. 如图,内接于是直径,过点A作的切线 . 若 , 则的度数是度.
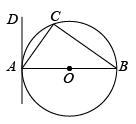 12. 如图,、是的弦,过点A的切线交的延长线于点 , 若 , 则°.
12. 如图,、是的弦,过点A的切线交的延长线于点 , 若 , 则°.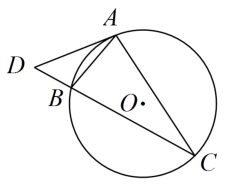 13. 中国元代数学家朱世杰所著《四元玉鉴》记载有“锁套吞容”之“方田圆池结角池图”.“方田一段,一角圆池占之.”意思是说:“一块正方形田地,在其一角有一个圆形的水池(其中圆与正方形一角的两边均相切)”,如图所示.问题:此图中,正方形一条对角线与⊙相交于点、(点在点的右上方),若的长度为10丈,⊙的半径为2丈,则的长度为丈.
13. 中国元代数学家朱世杰所著《四元玉鉴》记载有“锁套吞容”之“方田圆池结角池图”.“方田一段,一角圆池占之.”意思是说:“一块正方形田地,在其一角有一个圆形的水池(其中圆与正方形一角的两边均相切)”,如图所示.问题:此图中,正方形一条对角线与⊙相交于点、(点在点的右上方),若的长度为10丈,⊙的半径为2丈,则的长度为丈.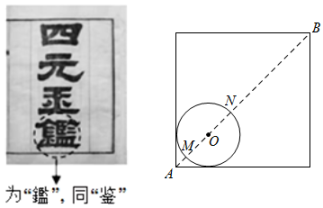 14. 如图, 是 的直径, 是 的切线, 为切点,连接 ,与 交于点 ,连接 .若 ,则 .
14. 如图, 是 的直径, 是 的切线, 为切点,连接 ,与 交于点 ,连接 .若 ,则 . 15. 如图,在△ABC中,AC=2,BC=4,点O在BC上,以OB为半径的圆与AC相切于点A.D是BC边上的动点,当△ACD为直角三角形时,AD的长为
15. 如图,在△ABC中,AC=2,BC=4,点O在BC上,以OB为半径的圆与AC相切于点A.D是BC边上的动点,当△ACD为直角三角形时,AD的长为 16. 如图,木工用角尺的短边紧靠⊙О于点A,长边与⊙О相切于点B,角尺的直角顶点为C,已知AC=6cm,CB=8cm,则⊙О的半径为cm.
16. 如图,木工用角尺的短边紧靠⊙О于点A,长边与⊙О相切于点B,角尺的直角顶点为C,已知AC=6cm,CB=8cm,则⊙О的半径为cm.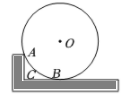
三、解答题(共8题,共72分)
-
17. 如图,在中,以AB为直径作交AC、BC于点D、E,且D是AC的中点,过点D作于点G,交BA的延长线于点H.
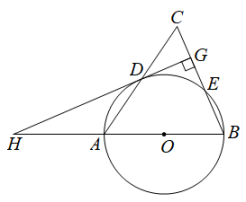 (1)、求证:直线HG是的切线;(2)、若 , 求CG的长.18. 如图,在半径为10cm的⊙O中,AB是⊙O的直径,CD是过⊙O上一点C的直线,且AD⊥DC于点D,AC平分∠BAD,点E是BC的中点,OE=6cm.
(1)、求证:直线HG是的切线;(2)、若 , 求CG的长.18. 如图,在半径为10cm的⊙O中,AB是⊙O的直径,CD是过⊙O上一点C的直线,且AD⊥DC于点D,AC平分∠BAD,点E是BC的中点,OE=6cm. (1)、求证:CD是⊙O的切线;(2)、求AD的长.19. 如图,AB是⊙O的直径,点E在⊙O上,连接AE和BE,BC平分∠ABE交⊙O于点C,过点C作CD⊥BE,交BE的延长线于点D,连接CE.
(1)、求证:CD是⊙O的切线;(2)、求AD的长.19. 如图,AB是⊙O的直径,点E在⊙O上,连接AE和BE,BC平分∠ABE交⊙O于点C,过点C作CD⊥BE,交BE的延长线于点D,连接CE.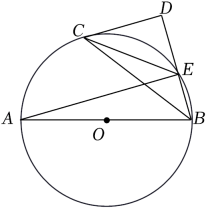 (1)、请判断直线CD与⊙O的位置关系,并说明理由;(2)、若sin∠ECD= , CE=5,求⊙O的半径.20. 如图,以AB为直径的⊙O与△ABC的边BC相切于点B,且与AC边交于点D,点E为BC中点,连接DE、BD.
(1)、请判断直线CD与⊙O的位置关系,并说明理由;(2)、若sin∠ECD= , CE=5,求⊙O的半径.20. 如图,以AB为直径的⊙O与△ABC的边BC相切于点B,且与AC边交于点D,点E为BC中点,连接DE、BD.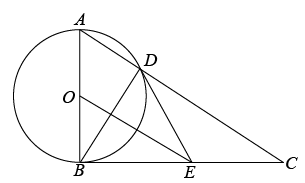 (1)、求证:DE是⊙O的切线;(2)、若DE=5,cos∠ABD= , 求OE的长.21. 如图,是的外接圆,为的直径,点为上一点,交的延长线于点 , 与交于点 , 连接 , 若 .
(1)、求证:DE是⊙O的切线;(2)、若DE=5,cos∠ABD= , 求OE的长.21. 如图,是的外接圆,为的直径,点为上一点,交的延长线于点 , 与交于点 , 连接 , 若 .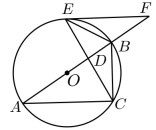 (1)、求证:是的切线.(2)、若 , , 求的半径.22. 如图,AC是⊙O的直径,弦BD交AC于点E,点F为BD延长线上一点,∠DAF=∠B.
(1)、求证:是的切线.(2)、若 , , 求的半径.22. 如图,AC是⊙O的直径,弦BD交AC于点E,点F为BD延长线上一点,∠DAF=∠B.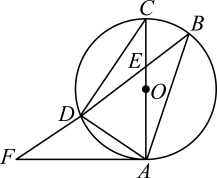 (1)、求证:AF是⊙O的切线;(2)、若⊙O的半径为5,AD是AEF的中线,且AD=6,求AE的长.
(1)、求证:AF是⊙O的切线;(2)、若⊙O的半径为5,AD是AEF的中线,且AD=6,求AE的长.