2023年中考数学精选真题实战测试52 圆的基本概念 B
试卷更新日期:2023-02-25 类型:二轮复习
一、单选题(每题3分,共30分)
-
1. 如图,AB是⊙O的直径,C、D是⊙O上的两点,若∠CAB=65°,则∠ADC的度数为( )
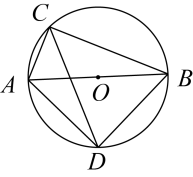 A、25° B、35° C、45° D、65°2. 如图,内接于⊙ , 连接 , 则( )
A、25° B、35° C、45° D、65°2. 如图,内接于⊙ , 连接 , 则( )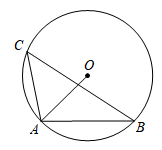 A、 B、 C、 D、3. 如图,四边形 内接于⊙ , 为⊙ 的直径, ,则 的度数是( )
A、 B、 C、 D、3. 如图,四边形 内接于⊙ , 为⊙ 的直径, ,则 的度数是( )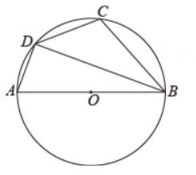 A、90° B、100° C、110° D、120°4. 如图,为的直径,弦交于点 , , , , 则( )
A、90° B、100° C、110° D、120°4. 如图,为的直径,弦交于点 , , , , 则( )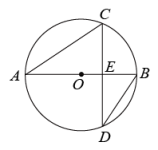 A、 B、 C、1 D、25. 将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A,B的读数分别为86°,30°,则∠ACB的度数是( )
A、 B、 C、1 D、25. 将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A,B的读数分别为86°,30°,则∠ACB的度数是( )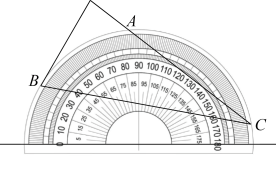 A、28° B、30° C、36° D、56°6. 如图,在中, , , . 以点为圆心,为半径作圆,当点在内且点在外时,的值可能是( )
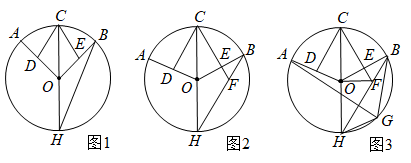
A、28° B、30° C、36° D、56°6. 如图,在中, , , . 以点为圆心,为半径作圆,当点在内且点在外时,的值可能是( )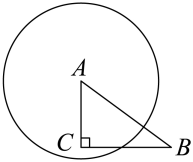 A、2 B、3 C、4 D、57. 如图, 是 的外接圆,且 ,在弧AB上取点D(不与点A,B重合),连接 ,则 的度数是( )
A、2 B、3 C、4 D、57. 如图, 是 的外接圆,且 ,在弧AB上取点D(不与点A,B重合),连接 ,则 的度数是( )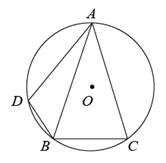 A、60° B、62° C、72° D、73°8. 如图,⊙O是等边△ABC的外接圆,若AB=3,则⊙O的半径是( )
A、60° B、62° C、72° D、73°8. 如图,⊙O是等边△ABC的外接圆,若AB=3,则⊙O的半径是( )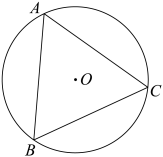 A、 B、 C、 D、9. 如图,已知△ABC内接于半径为1的⊙O,∠BAC=θ(θ是锐角),则△ABC的面积的最大值为( )
A、 B、 C、 D、9. 如图,已知△ABC内接于半径为1的⊙O,∠BAC=θ(θ是锐角),则△ABC的面积的最大值为( )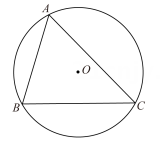 A、cosθ(1+cosθ) B、cosθ(1+sinθ) C、sinθ(1+sinθ) D、sinθ(1+cosθ)10. 如图,点 是 的内心, 的延长线和 的外接圆相交于点 ,与 相交于点 ,则下列结论:① ;②若 ,则 ;③若点 为 的中点,则 ;④ .其中一定正确的个数是( )
A、cosθ(1+cosθ) B、cosθ(1+sinθ) C、sinθ(1+sinθ) D、sinθ(1+cosθ)10. 如图,点 是 的内心, 的延长线和 的外接圆相交于点 ,与 相交于点 ,则下列结论:① ;②若 ,则 ;③若点 为 的中点,则 ;④ .其中一定正确的个数是( )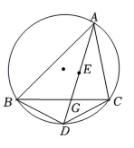 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题(每空3分,共18分)
-
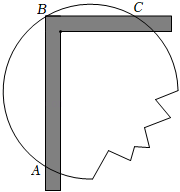
11. 已知⊙O的直径AB长为2,弦AC长为 , 那么弦AC所对的圆周角的度数等于 .12. 一圆形玻璃镜面损坏了一部分,为得到同样大小的镜面,工人师傅用直角尺作如图所示的测量,测得AB=12cm,BC=5cm,则圆形镜面的半径为 .
 13. 如图,是的内接三角形.若 , , 则的半径是.
13. 如图,是的内接三角形.若 , , 则的半径是. 14. 如图,在边长为1的正方形网格中,⊙O是△ABC的外接圆,点A,B,O在格点上,则cos∠ACB的值是 .
14. 如图,在边长为1的正方形网格中,⊙O是△ABC的外接圆,点A,B,O在格点上,则cos∠ACB的值是 .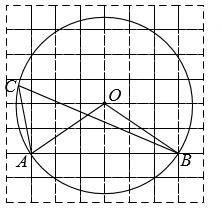 15. 如图, 是 的直径,点 在 上,若 ,则 °.
15. 如图, 是 的直径,点 在 上,若 ,则 °. 16. 如图,在平面直角坐标系 中,点A在 轴负半轴上,点B在 轴正半轴上,⊙D经过A , B , O , C四点,∠ACO=120°,AB=4,则圆心点D的坐标是
16. 如图,在平面直角坐标系 中,点A在 轴负半轴上,点B在 轴正半轴上,⊙D经过A , B , O , C四点,∠ACO=120°,AB=4,则圆心点D的坐标是
三、解答题(共8题,共72分)
-
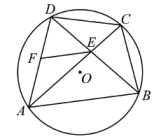
17. 如图,边长为6的等边三角形ABC内接于⊙O,点D为AC上的动点(点A、C除外),BD的延长线交⊙O于点E,连接CE.
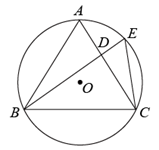 (1)、求证 ;(2)、当 时,求CE的长.18. 如图,在⊙O中,直径AB与弦CD相交于点E,连接AC、BD.
(1)、求证 ;(2)、当 时,求CE的长.18. 如图,在⊙O中,直径AB与弦CD相交于点E,连接AC、BD.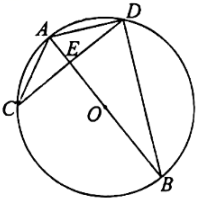 (1)、求证:△AEC∽△DEB;(2)、连接AD,若AD=3,∠C=30°,求⊙O的半径.19. 如图,△ABC内接于⊙O,交⊙O于点D,交BC于点E,交⊙O于点F,连接AF,CF.
(1)、求证:△AEC∽△DEB;(2)、连接AD,若AD=3,∠C=30°,求⊙O的半径.19. 如图,△ABC内接于⊙O,交⊙O于点D,交BC于点E,交⊙O于点F,连接AF,CF.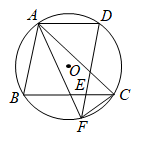 (1)、求证:AC=AF;(2)、若⊙O的半径为3,∠CAF=30°,求的长(结果保留π).20. 如图,正方形内接于 , 点E为的中点,连接交于点F,延长交于点G,连接.
(1)、求证:AC=AF;(2)、若⊙O的半径为3,∠CAF=30°,求的长(结果保留π).20. 如图,正方形内接于 , 点E为的中点,连接交于点F,延长交于点G,连接.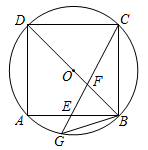 (1)、求证:;(2)、若.求和的长.21. 如图,以为直径的经过的顶点 , , 分别平分和 , 的延长线交于点 , 连接.
(1)、求证:;(2)、若.求和的长.21. 如图,以为直径的经过的顶点 , , 分别平分和 , 的延长线交于点 , 连接.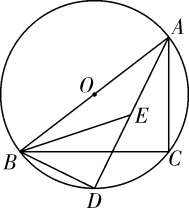 (1)、判断的形状,并证明你的结论;(2)、若 , , 求的长.22. 如图,点在以为直径的上,平分交于点 , 交于点 , 过点作的切线交的延长线于点.
(1)、判断的形状,并证明你的结论;(2)、若 , , 求的长.22. 如图,点在以为直径的上,平分交于点 , 交于点 , 过点作的切线交的延长线于点.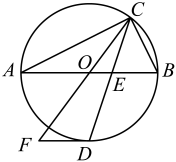 (1)、求证:;(2)、若 , , 求的长.
(1)、求证:;(2)、若 , , 求的长.