2023年中考数学精选真题实战测试47 图形的相似 A
试卷更新日期:2023-02-25 类型:二轮复习
一、单选题(每题3分,共30分)
-
1. 如图,若方格纸中每个小正方形的边长均为1,则阴影部分的面积为( )
 A、5 B、6 C、 D、2. 西周数学家商高总结了用“矩”(如图1)测量物高的方法:把矩的两边放置成如图2的位置,从矩的一端A(人眼)望点E,使视线通过点C,记人站立的位置为点B,量出BG长,即可算得物高EG.令BG=x(m), EG=y(m),若a=30cm,b=60cm,AB=1.6m,则y关于x的函数表达式为( )
A、5 B、6 C、 D、2. 西周数学家商高总结了用“矩”(如图1)测量物高的方法:把矩的两边放置成如图2的位置,从矩的一端A(人眼)望点E,使视线通过点C,记人站立的位置为点B,量出BG长,即可算得物高EG.令BG=x(m), EG=y(m),若a=30cm,b=60cm,AB=1.6m,则y关于x的函数表达式为( )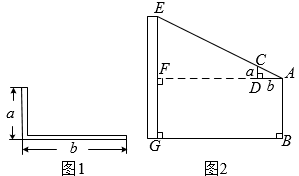 A、 B、 C、 D、3. 如图,在平面直角坐标系中,为的边上一点, , 过作交于点 , 、两点纵坐标分别为1、3,则点的纵坐标为( )
A、 B、 C、 D、3. 如图,在平面直角坐标系中,为的边上一点, , 过作交于点 , 、两点纵坐标分别为1、3,则点的纵坐标为( )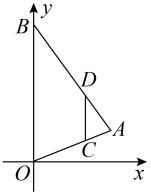 A、4 B、5 C、6 D、74. 如图,点D为边上任一点,交于点E,连接相交于点F,则下列等式中不成立的是( )
A、4 B、5 C、6 D、74. 如图,点D为边上任一点,交于点E,连接相交于点F,则下列等式中不成立的是( ) A、 B、 C、 D、5. 如图,在中,是边上的点, , , 则与的周长比是( )
A、 B、 C、 D、5. 如图,在中,是边上的点, , , 则与的周长比是( ) A、 B、 C、 D、6. 的边上有、、三点,各点位置如图所示.若 , , , 则根据图中标示的长度,求四边形与的面积比为何?( )
A、 B、 C、 D、6. 的边上有、、三点,各点位置如图所示.若 , , , 则根据图中标示的长度,求四边形与的面积比为何?( )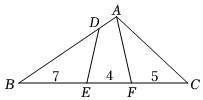 A、1:3 B、1:4 C、2:5 D、3:87. 如图,点E在矩形 的 边上,将 沿 翻折,点A恰好落在 边上的点F处,若 , ,则 的长为( )
A、1:3 B、1:4 C、2:5 D、3:87. 如图,点E在矩形 的 边上,将 沿 翻折,点A恰好落在 边上的点F处,若 , ,则 的长为( ) A、9 B、12 C、15 D、188. 如图,正方形ABCD与正方形BEFG有公共顶点B,连接EC、GA,交于点O,GA与BC交于点P,连接OD、OB,则下列结论一定正确的是( )
A、9 B、12 C、15 D、188. 如图,正方形ABCD与正方形BEFG有公共顶点B,连接EC、GA,交于点O,GA与BC交于点P,连接OD、OB,则下列结论一定正确的是( )①EC⊥AG;②△OBP∽△CAP;③OB平分∠CBG;④∠AOD=45°;
 A、①③ B、①②③ C、②③ D、①②④9. 如图,在菱形 中, 是 的中点, ,交 于点 ,如果 ,那么菱形 的周长是( )
A、①③ B、①②③ C、②③ D、①②④9. 如图,在菱形 中, 是 的中点, ,交 于点 ,如果 ,那么菱形 的周长是( )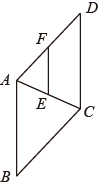 A、11 B、22 C、33 D、4410. 如图,四边形为正方形,将绕点逆时针旋转至 , 点 , , 在同一直线上,与交于点 , 延长与的延长线交于点 , , .以下结论:
A、11 B、22 C、33 D、4410. 如图,四边形为正方形,将绕点逆时针旋转至 , 点 , , 在同一直线上,与交于点 , 延长与的延长线交于点 , , .以下结论:①;②;③;④.其中正确结论的个数为( )
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题(每空3分,共18分)
-
11. 如图,在中,点在边上,点在边上,请添加一个条件 , 使.
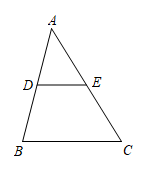 12. 如图,将矩形纸片ABCD折叠,折痕为MN,点M,N分别在边AD,BC上,点C,D的对应点分别在E,F且点F在矩形内部,MF的延长线交BC与点G,EF交边BC于点H. , , 当点H为GN三等分点时,MD的长为 .
12. 如图,将矩形纸片ABCD折叠,折痕为MN,点M,N分别在边AD,BC上,点C,D的对应点分别在E,F且点F在矩形内部,MF的延长线交BC与点G,EF交边BC于点H. , , 当点H为GN三等分点时,MD的长为 .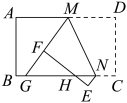 13. 如图, , , 相交于点 , 若 , , 则的长为 .
13. 如图, , , 相交于点 , 若 , , 则的长为 .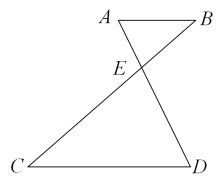 14. 如图,在中,点F、G在上,点E、H分别在、上,四边形是矩形,是的高. , 那么的长为 .
14. 如图,在中,点F、G在上,点E、H分别在、上,四边形是矩形,是的高. , 那么的长为 .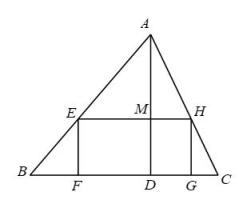 15. 如图,在矩形中,若 , 则的长为 .
15. 如图,在矩形中,若 , 则的长为 . 16. 如图,在中, , , .在中, , , .用一条始终绷直的弹性染色线连接 , 从起始位置(点与点重合)平移至终止位置(点与点重合),且斜边始终在线段上,则的外部被染色的区域面积是.
16. 如图,在中, , , .在中, , , .用一条始终绷直的弹性染色线连接 , 从起始位置(点与点重合)平移至终止位置(点与点重合),且斜边始终在线段上,则的外部被染色的区域面积是.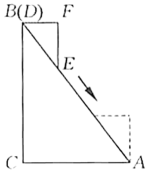
三、解答题(共8题,共72分)
-
17. 如图,在与中,点、分别在边、上,且 , 若 ▲ , 则 . 请从①;②;③这三个选项中选择一个作为条件(写序号),并加以证明.
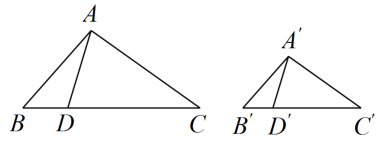 18. 如图所示,在等腰三角形ABC中,AB=AC,点E,F在线段BC上,点Q在线段AB上,且CF=BE,AE²=AQ·AB求证:
18. 如图所示,在等腰三角形ABC中,AB=AC,点E,F在线段BC上,点Q在线段AB上,且CF=BE,AE²=AQ·AB求证: (1)、∠CAE=∠BAF;(2)、CF·FQ=AF·BQ19. 如图,在矩形 中, ,点E是 边上的任一点(不包括端点D,C),过点A作 交 的延长线于点F,设 .
(1)、∠CAE=∠BAF;(2)、CF·FQ=AF·BQ19. 如图,在矩形 中, ,点E是 边上的任一点(不包括端点D,C),过点A作 交 的延长线于点F,设 .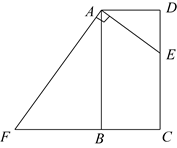 (1)、求 的长(用含a的代数式表示);(2)、连接 交 于点G,连接 ,当 时,求证:四边形 是菱形.20. 我们经常会采用不同方法对某物体进行测量,请测量下列灯杆AB的长.
(1)、求 的长(用含a的代数式表示);(2)、连接 交 于点G,连接 ,当 时,求证:四边形 是菱形.20. 我们经常会采用不同方法对某物体进行测量,请测量下列灯杆AB的长. (1)、如图1所示,将一个测角仪放置在距离灯杆AB底部a米的点D处,测角仪高为b米,从C点测得A点的仰角为α,求灯杆AB的高度.(用含a,b,a的代数式表示)(2)、我国古代数学家赵爽利用影子对物体进行测量的方法,在至今仍有借鉴意义图2所示,现将一高度为2米的木杆CG放在灯杆AB前,测得其影长CH为1米,再将木杆沿着BC方向移动1.8米至DE的位置,此时测得其影长DF为3米,求灯杆AB的高度21. 如图①、图②、图③均是的正方形网格,每个小正方形的边长均为1,其顶点称为格点,的顶点均在格点上.只用无刻度的直尺,在给定的网格中,按下列要求作图,保留作图痕迹.
(1)、如图1所示,将一个测角仪放置在距离灯杆AB底部a米的点D处,测角仪高为b米,从C点测得A点的仰角为α,求灯杆AB的高度.(用含a,b,a的代数式表示)(2)、我国古代数学家赵爽利用影子对物体进行测量的方法,在至今仍有借鉴意义图2所示,现将一高度为2米的木杆CG放在灯杆AB前,测得其影长CH为1米,再将木杆沿着BC方向移动1.8米至DE的位置,此时测得其影长DF为3米,求灯杆AB的高度21. 如图①、图②、图③均是的正方形网格,每个小正方形的边长均为1,其顶点称为格点,的顶点均在格点上.只用无刻度的直尺,在给定的网格中,按下列要求作图,保留作图痕迹.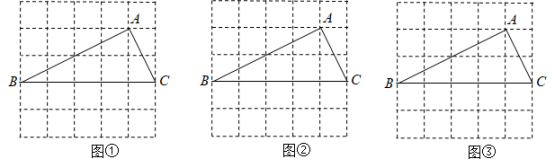 (1)、网格中的形状是;(2)、在图①中确定一点D,连结、 , 使与全等:(3)、在图②中的边上确定一点E,连结 , 使:(4)、在图③中的边上确定一点P,在边BC上确定一点Q,连结 , 使 , 且相似比为1:2.22. 如图,矩形ABCD中,AB=15,BC=9,E是CD边上一点(不与点C重合),作AF⊥BE于F,CG⊥BE于G,延长CG至点C′,使C′G=CG,连接CF,AC′.
(1)、网格中的形状是;(2)、在图①中确定一点D,连结、 , 使与全等:(3)、在图②中的边上确定一点E,连结 , 使:(4)、在图③中的边上确定一点P,在边BC上确定一点Q,连结 , 使 , 且相似比为1:2.22. 如图,矩形ABCD中,AB=15,BC=9,E是CD边上一点(不与点C重合),作AF⊥BE于F,CG⊥BE于G,延长CG至点C′,使C′G=CG,连接CF,AC′. (1)、直接写出图中与△AFB相似的一个三角形;(2)、若四边形AFCC′是平行四边形,求CE的长;(3)、当CE的长为多少时,以C′,F,B为顶点的三角形是以C′F为腰的等腰三角形?23. 在△ABC中,∠BAC=90°,AB=AC,直线l经过点A,过点B、C分别作l的垂线,垂足分别为点D、E.
(1)、直接写出图中与△AFB相似的一个三角形;(2)、若四边形AFCC′是平行四边形,求CE的长;(3)、当CE的长为多少时,以C′,F,B为顶点的三角形是以C′F为腰的等腰三角形?23. 在△ABC中,∠BAC=90°,AB=AC,直线l经过点A,过点B、C分别作l的垂线,垂足分别为点D、E. (1)、特例体验:如图①,若直线l∥BC,AB=AC= ,分别求出线设BD、CE和DE的长;(2)、规律探究:
(1)、特例体验:如图①,若直线l∥BC,AB=AC= ,分别求出线设BD、CE和DE的长;(2)、规律探究:(Ⅰ)如图②,若直线l从图①状态开始绕点A旋转α(0<α<45°),请探究线段BD、CE和DE的数量关系并说明理由;
(Ⅱ)如图③,若直线l从图①状态开始绕点A顺时针旋转α(45°<α<90°),与线段BC相交于点H,请再探线段BD、CE和DE的数量关系并说明理由;
(3)、尝试应用:在图③中,延长线设BD交线段AC于点F,若CE=3,DE=1,求S△BFC .24. 如图 (1)、如图1,在△ABC中, ,CD平分 ,交AB于点D, // ,交BC于点E.
(1)、如图1,在△ABC中, ,CD平分 ,交AB于点D, // ,交BC于点E.①若 , ,求BC的长;
②试探究 是否为定值.如果是,请求出这个定值;如果不是,请说明理由.
(2)、如图2, 和 是△ABC的2个外角, ,CD平分 ,交AB的延长线于点D, // ,交CB的延长线于点E.记△ACD的面积为 ,△CDE的面积为 ,△BDE的面积为 .若 ,求 的值.