重庆市2023届高三下学期数学开学摸底试卷
试卷更新日期:2023-02-24 类型:开学考试
一、单选题
-
1. 设集合 , , 则( )A、 B、 C、 D、2. 复数z在复平面内对应的点的坐标为 , 则( )A、 B、 C、 D、3. 函数的图象大致是( )A、
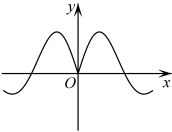 B、
B、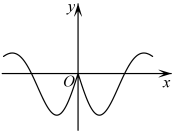 C、
C、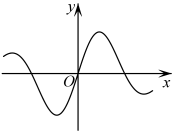 D、
D、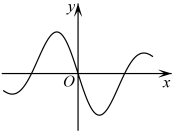 4. 如图,在直三棱柱中,是直角三角形,且 , 为棱的中点,点在棱上,且 , 则异面直线AC与DE所成角的余弦值是( )
4. 如图,在直三棱柱中,是直角三角形,且 , 为棱的中点,点在棱上,且 , 则异面直线AC与DE所成角的余弦值是( )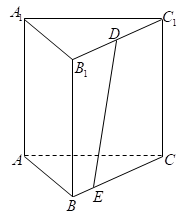 A、 B、 C、 D、5. 设等差数列的前项和为 , 满足 , 则( )A、 B、的最小值为 C、 D、满足的最大自然数的值为256. 从编号分别为1、2、3、4、5、6、7的七个大小完全相同的小球中,随机取出三个小球,则至少有两个小球编号相邻的概率为( )A、 B、 C、 D、7. 已知函数 ,则函数 的零点个数是( )A、2 B、3 C、4 D、58. 已知两条直线 , , 有一动圆(圆心和半径都在变动)与都相交,并且被截在圆内的两条线段的长度分别是定值26,24,则动圆圆心的轨迹方程为( )A、 B、 C、 D、
A、 B、 C、 D、5. 设等差数列的前项和为 , 满足 , 则( )A、 B、的最小值为 C、 D、满足的最大自然数的值为256. 从编号分别为1、2、3、4、5、6、7的七个大小完全相同的小球中,随机取出三个小球,则至少有两个小球编号相邻的概率为( )A、 B、 C、 D、7. 已知函数 ,则函数 的零点个数是( )A、2 B、3 C、4 D、58. 已知两条直线 , , 有一动圆(圆心和半径都在变动)与都相交,并且被截在圆内的两条线段的长度分别是定值26,24,则动圆圆心的轨迹方程为( )A、 B、 C、 D、二、多选题
-
9. 下列命题中,正确的命题是( )A、数据1,2,3,4,5,6,7,8,9,10的分位数是7 B、若随机变量 , 则 C、若事件A,B满足 , 则A与B独立 D、若随机变量 , , 则10. 已知函数的最小正周期为 , 将的图象向左平移个单位长度,再把得到的曲线上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数的图象,则下列结论正确的是( )A、 B、在单调递增 C、的图象关于对称 D、在上的最大值是111. 已知抛物线的焦点为F,过原点O的动直线l交抛物线于另一点P,交抛物线的准线于点Q,下列说法正确的是( )A、若O为线段中点,则 B、若 , 则 C、存在直线l,使得 D、△PFO面积的最小值为212. 定义:在区间上,若函数是减函数,且是增函数,则称在区间上是“弱减函数”.根据定义可得( )A、在上是“弱减函数” B、在上是“弱减函数” C、若在上是“弱减函数”,则 D、若在上是“弱减函数”,则
三、填空题
-
13. 已知向量 , , 若 , 则实数 .14. 将3封不同的信随机放入2个不同的信箱中,共有种不同的放法,则在的展开式中,含项的系数为 .15. 《数书九章》三斜求积术:“以小斜幂,并大斜幂,减中斜幂,余半之,自乘于上;以小斜幂乘大斜幂,减上,余四约一,为实,一为从隅,开平方得积”.秦九韶把三角形的三条边分别称为小斜、中斜和大斜,“术”即方法.以 , , , 分别表示三角形的面积,大斜,中斜,小斜;分别为对应的大斜,中斜,小斜上的高;则 . 若在中 , , , 根据上述公式,可以推出该三角形外接圆的半径为 .16. 定义:若A,B,C,D为球面上四点,E,F分别是AB,CD的中点,则把以EF为直径的球称为AB,CD的“伴随球”.已知A,B,C,D是半径为2的球面上四点, , 则AB,CD的“伴随球”的直径取值范围为;若A,B,C,D不共面,则四面体ABCD体积的最大值为.
四、解答题
-
17. 如图,△ABC中,角A,B,C的对边分别为a,b,c,且.
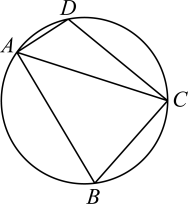 (1)、求角B的大小;(2)、已知 , 若D为△ABC外接圆劣弧AC上一点,求AD+DC的最大值.18. 已知数列满足 , .(1)、设 , 证明:是等差数列;(2)、设数列的前n项和为 , 求 .19. 如图1,在平面四边形中,∥ , , 将沿翻折到的位置,使得平面⊥平面 , 如图2所示.
(1)、求角B的大小;(2)、已知 , 若D为△ABC外接圆劣弧AC上一点,求AD+DC的最大值.18. 已知数列满足 , .(1)、设 , 证明:是等差数列;(2)、设数列的前n项和为 , 求 .19. 如图1,在平面四边形中,∥ , , 将沿翻折到的位置,使得平面⊥平面 , 如图2所示.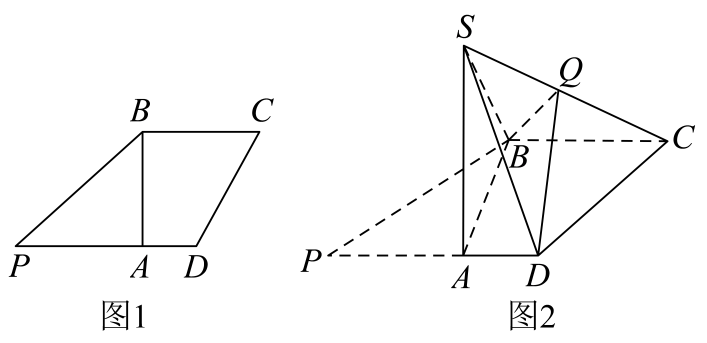 (1)、设平面与平面的交线为 , 求证:;(2)、在线段上是否存在一点(点不与端点重合),使得二面角的余弦值为 , 请说明理由.20. 某企业从生产的一批零件中抽取100件产品作为样本,检测其质量指标值m(其中:),得到频率分布直方图,并依据质量指标值划分等级如表所示:
(1)、设平面与平面的交线为 , 求证:;(2)、在线段上是否存在一点(点不与端点重合),使得二面角的余弦值为 , 请说明理由.20. 某企业从生产的一批零件中抽取100件产品作为样本,检测其质量指标值m(其中:),得到频率分布直方图,并依据质量指标值划分等级如表所示: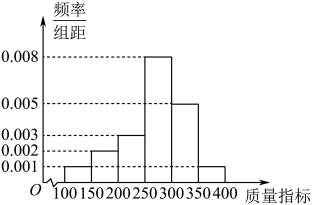
质量指标值m
150≤m<350
100≤m<150或350≤m≤400
等级
A级
B级
(1)、根据频率分布直方图估计产品的质量指标值的分位数;(2)、从样本的B级零件中随机抽3件,记其中质量指标值在[350,400]的零件的件数为 , 求的分布列和数学期望;(3)、该企业为节省检测成本,采用混装的方式将所有的零件按500个一箱包装,已知一个A级零件的利润是10元,一个B级零件的利润是5元,以样本分布的频率作为总体分布的概率,试估计每箱零件的利润.