浙江省绍兴市嵊州市2023届高三下学期数学2月学业质量调测试卷

试卷更新日期：2023-02-24 类型：开学考试

进入出卷网下载

一、单选题

1. 已知集合 $A = {x ∣ x^{2} + x - 2 \leq 0} ， B = {x ∣ 0 < x \leq 2}$ ，则 $A \cup B =$ （）

A、 ${x ∣ 0 < x \leq 1}$ B、 ${x ∣ 0 < x \leq 2}$ C、 ${x ∣ - 1 \leq x \leq 2}$ D、 ${x ∣ - 2 \leq x \leq 2}$

查看试题解析
2. 已知双曲线 $\frac{y^{2}}{2} - x^{2} = 1$ ，则该双曲线的其中一条渐近线方程是（）

A、 $y = \frac{1}{2} x$ B、 $y = \frac{\sqrt{2}}{2} x$ C、 $y = \sqrt{2} x$ D、 $y = 2 x$

查看试题解析
3. 若 $\frac{2 a + 2 i}{1 - i} = b i$ （ $a ， b \in R ， i$ 是虚数单位），则 $a - b =$ （）

A、 $- 1$ B、0 C、1 D、3

查看试题解析
4. 已知 $△ A B C$ 是边长为1的等边三角形，点 $D ， E$ 分别是边 $A B ， B C$ 的中点，连接 $D E$ 并延长到点 $F$ ，使得 $D E = E F$ ，则 $\vec{A F} \cdot \vec{B C}$ 的值为（）

A、 $- \frac{1}{4}$ B、 $\frac{1}{4}$ C、 $\frac{1}{2}$ D、1

查看试题解析
5. 某中学为了解高三男生的体能情况，通过随机抽样，获得了200名男生的100米体能测试成绩（单位：秒），将数据按照 $[11.5 ， 12) ， [12 ， 12.5) ， ⋯ ， [15.5 ， 16]$ 分成9组，制成了如图所示的频率分布直方图.
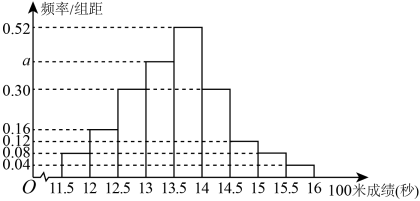
由直方图可估计本校高三男生100米体能测试成绩小于13.5秒的人数为（）

A、47 B、54 C、67 D、94

查看试题解析
6. 已知不重合的平面 $α, β, γ$ 和直线 $l$ ，则“ $α / / β$ ”的充分不必要条件是（）

A、 $α$ 内有无数条直线与 $β$ 平行 B、 $l ⊥ α$ 且 $l ⊥ β$ C、 $α ⊥ γ$ 且 $γ ⊥ β$ D、 $α$ 内的任何直线都与 $β$ 平行

查看试题解析
7. 在正棱台 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $A B = 2 A_{1} B_{1} ， A A_{1} = \sqrt{3} ， M$ 为棱 $B_{1} C_{1}$ 中点.当四棱台的体积最大时，平面 $M B D$ 截该四棱台的截面面积是（）

A、 $\frac{5 \sqrt{3}}{4}$ B、 $3 \sqrt{2}$ C、 $\frac{5 \sqrt{3}}{2}$ D、 $6 \sqrt{2}$

查看试题解析
8. 对于任意实数 $x$ 及 $1 \leq t \leq \sqrt{3}$ ，均有 ${(x + t^{2} + 1)}^{2} + (x + a t)^{2} \geq \frac{1}{8}$ ，则实数 $a$ 的取值范围是（）

A、 $(- ∞ ， \sqrt{2}] \cup [\frac{5}{2} ， + ∞)$ B、 $(- ∞ ， \frac{3}{2}] \cup [\frac{5}{2} ， + ∞)$ C、 $(- ∞ ， \sqrt{2}] \cup [\frac{3 \sqrt{3}}{2} ， + ∞)$ D、 $(- ∞ ， \frac{3}{2}] \cup [\frac{3 \sqrt{3}}{2} ， + ∞)$

查看试题解析

二、多选题

9. 已知函数 $f (x) = s i n 2 x + \sqrt{3} c o s 2 x$ ，则（）

A、 $f (x)$ 的最小正周期为 $π$ B、 $f (x)$ 的一个对称中心坐标为 $(- \frac{π}{6} ， 0)$ C、 $f (x)$ 的图象可由函数 $g (x) = 2 s i n 2 x$ 的图象向左平移 $\frac{π}{12}$ 个单位得到 D、 $f (x)$ 在区间 $[\frac{π}{12} ， \frac{7 π}{12}]$ 上单调递减

查看试题解析
10. 传说古希腊毕达哥拉斯学派的数学家用沙粒和小石子来研究数，他们根据沙粒或小石子所排列的形状把数分成许多类，如图中第一行的1，3，6，10称为三角形数，第二行的1，4，9，16称为正方形数.下列数中，既是三角形数又是正方形数的是（）

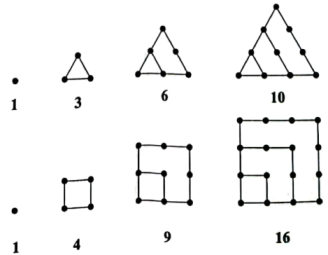A、36 B、289 C、1225 D、1378

查看试题解析
11. 过直线 $l ： x = - 2$ 上一点 $P$ 作拋物线 $y^{2} = 6 x$ 的两条切线，设切点分别为 $A ， B$ ，记 $M$ 是线段 $A B$ 的中点，则（）

A、直线 $A B$ 经过该抛物线的焦点 B、直线 $P M ∥ x$ 轴 C、线段 $P M$ 的中点在该抛物线上 D、以线段 $A B$ 为直径的圆与抛物线的准线相交

查看试题解析
12. 已知 $x > 0 ， y > 0$ ，若 $e^{x} + l n y = 2 x + y$ ，则（）

A、 $x > 1$ B、 $y > e$ C、 $x < e^{y}$ D、 $y < e^{x}$

查看试题解析

三、填空题

13. 若 ${(x^{2} - \frac{1}{x \sqrt{x}})}^{n}$ 的展开式中含有非零常数项，则正整数 $n$ 的最小值为.

查看试题解析
14. 已知函数 $f (x)$ 满足： $f (x y) = f (x) + f (y)$ ，且当 $x > y$ 时， $f (x) < f (y)$ ，请你写出符合上述条件的一个函数 $f (x) =$ .

查看试题解析
15. 已知圆 $C_{1} ： x^{2} + y^{2} = 1$ 和圆 $C_{2} ： (x - 3)^{2} + (y - 4)^{2} = r^{2} (r > 0)$ ，若对于 $C_{1}$ 上的任意一点 $P$ ，使得过点 $P$ 都可作一条射线与圆 $C_{2}$ 依次交于点 $A ， B$ ，满足 $| P A | = | A B |$ ，则 $r$ 的取值范围是.

查看试题解析
16. 在正三棱锥 $P - A B C$ 中， $P A = \sqrt{3}$ ，设 $M ， N$ 分别是棱 $P A ， A B$ 的中点， $O$ 是三棱锥 $P - A B C$ 的外接球的球心，若 $M N ⊥ M C$ ，则 $O$ 到平面 $A B C$ 的距离为.

查看试题解析

四、解答题

17. 设等比数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ，已知 $S_{6} = 9 S_{3} ， S_{2} = 3$ .

(1)、求数列 ${a_{n}}$ 通项公式；

(2)、记 $b_{n} = \frac{1}{l o g_{2} a_{n + 1} \cdot l o g_{2} a_{n + 2}} ， n \in N^{*}$ ，证明： $b_{1} + b_{2} + ⋯ + b_{n} < 1$ .

查看试题解析
18. 如图，在直三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中， $E ， F$ 分别是棱 $A B ， B_{1} C_{1}$ 的中点， $∠ A C B = \frac{π}{2}$ .

(1)、证明： $E F ⊥ B C$ ；

(2)、若 $A C = 2 ， B C = 4$ ，平面 $A_{1} E F$ 与平面 $A B C$ 所成的锐二面角的角余弦值为 $\frac{1}{3}$ ，求直线 $E F$ 与平面 $A B C$ 所成角的正弦值.

查看试题解析
19. 原定于2022年9月在杭州举行的亚运会延期至2023年的9月，据调查此次亚运会已签约145家赞助企业，亚运会赞助成为一项跨度时间较长的营销方式，为了解其中在浙江地区的50家赞助企业每天销售额与每天线上销售时间之间的相关关系，某平台对50家赞助企业进行跟踪调查，其中每天线上销售时间不少于8小时的企业有30家，销售额不足50万元的企业有25家，统计后得到如下 $2 \times 2$ 列联表：

销售额不少于50万元
销售额不足50万元
合计
线上销售时间不少于8小时
17
30
线上销售时间不足8小时
合计
50
附：
$α$
$0.1$
$0.05$
$0.01$
$0.005$
$0.001$
$χ_{α}$
$2.706$
$3.841$
$6.635$
$7.879$
$10.828$
参考公式： $χ^{2} = \frac{n (a d - b c)^{2}}{(a + b) (c + d) (a + c) (b + d)}$ ，其中 $n = a + b + c + d$ .

(1)、请完成上面的 $2 \times 2$ 列联表，并依据 $α = 0.05$ 的独立性检验，能否认为赞助企业每天的销售额与每天线上销售时间有关；

(2)、（i）按销售额进行分层随机抽样，在线上销售时间不足8小时的赞助企业中抽取5家，求销售额不少于50万元和销售额不足50万元的企业数；
（ii）从销售额不少于50万元的企业抽取2家时，设抽到每天线上销售时间不足8小时的企业数是 $X$ ，求 $X$ 的分布列及期望值.

查看试题解析
20. 已知 $△ A B C$ 的内角 $A ， B ， C$ 的对边分别为 $a ， b ， c$ ，且 $c o s^{2} B - c o s^{2} C = s i n A \cdot (s i n A - s i n B)$ .

(1)、求角 $C$ 的大小；

(2)、若 $C D ⊥ A B$ 于 $D ， C D = \sqrt{3}$ ，求 $△ A B C$ 的面积的最小值.

查看试题解析
21. 在平面直角坐标系 $x O y$ 中，已知椭圆C： $\frac{x^{2}}{4} + y^{2} = 1 ， B (1 ， 0)$ .

(1)、设 $P$ 是椭圆 $C$ 上的一个动点，求 $\vec{P O} \cdot \vec{P B}$ 的取值范围；

(2)、设与坐标轴不垂直的直线 $l$ 交椭圆 $C$ 于 $M ， N$ 两点，试问：是否存在满足条件的直线 $l$ ，使得 $△ M B N$ 是以 $B$ 为直角顶点的等腰直角三角形？若存在，求出直线 $l$ 的方程，若不存在，请说明理由.

查看试题解析
22. 已知 $m > 0$ ，设函数 $f (x) = e^{x} \cdot (m l n x + 1)$ ， $f^{'} (x)$ 为 $f (x)$ 的导函数，且 $f^{'} (x) \geq \frac{5}{2} e^{x}$ 恒成立.

(1)、求实数 $m$ 的取值范围；

(2)、设 $f (x)$ 的零点为 $x_{0}$ ， $f^{'} (x)$ 的极小值点为 $x_{1}$ ，证明： $1 < \frac{x_{0}}{x_{1}} < e$ .

查看试题解析

	销售额不少于50万元	销售额不足50万元	合计
线上销售时间不少于8小时	17		30
线上销售时间不足8小时
合计			50

$α$	$0.1$	$0.05$	$0.01$	$0.005$	$0.001$
$χ_{α}$	$2.706$	$3.841$	$6.635$	$7.879$	$10.828$