浙江省名校协作体2023届高三下学期数学2月开学考试试卷

试卷更新日期：2023-02-24 类型：开学考试

进入出卷网下载

一、单选题

1. 已知集合 $A = {x ∣ x^{2} - 3 x < 0} ， B = {1 ， 2 ， 3 ， 4 ， 5}$ ，则 $(∁_{R} A) \cap B =$ （）

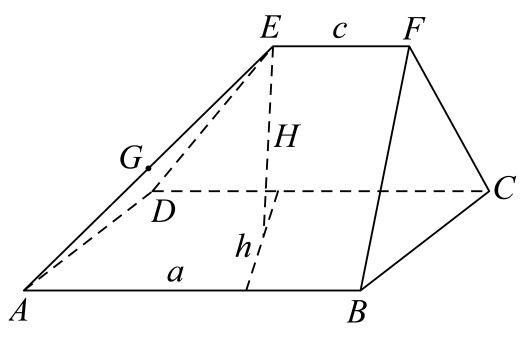
A、 ${1 ， 2}$ B、 ${4 ， 5}$ C、 ${3 ， 4 ， 5}$ D、 ${2 ， 3 ， 4 ， 5}$

查看试题解析
2. 已知复数z满足： $z (2 - i) = 1 - i$ ，则 $| z | =$ （）

A、 $\frac{\sqrt{2}}{5}$ B、 $\frac{\sqrt{10}}{5}$ C、 $\frac{\sqrt{15}}{5}$ D、 $\frac{3 \sqrt{2}}{5}$

查看试题解析
3. 若向量 $\vec{a} ， \vec{b}$ 满足 $| \vec{a} | = \sqrt{2} ， | \vec{b} | = 2 ， \vec{a} ⊥ (\vec{a} - \vec{b})$ ，则 $\vec{a}$ 与 $\vec{b}$ 的夹角为（）

A、 $\frac{π}{4}$ B、 $\frac{π}{3}$ C、 $\frac{2 π}{3}$ D、 $\frac{3 π}{4}$

查看试题解析
4. 设 $x$ ， $y$ 为正实数，若 $2 x + y + 2 x y = \frac{5}{4}$ ，则 $2 x + y$ 的最小值是（）

A、4 B、3 C、2 D、1

查看试题解析
5. 刍甍是如图所示五面体ABCDEF，其中 $A B ∥ C D ∥ E F$ ，底面ABCD是平行四边形，《九章算术·商功》对其体积有记载：“求积术曰，倍下袤，上袤从之，以广乘之，又以高乘之，六而一”，意思是：若 $E F = c ， A B = a$ ， AB、CD之间的距离是h，直线EF与平面ABCD之间的距离是H，则其体积 $V = \frac{H h (2 a + c)}{6}$ ，现有刍甍ABCDEF， $E F = 1 ， A B = 3$ ， AB、CD之间的距离是2，EF与平面ABCD之间的距离是4，过AE的中点G，作平面 $α ∥$ 平面ABCD，将该刍甍分为上下两部分，则上下体积之比为（）

A、 $1 ： 3$ B、 $1 ： 7$ C、 $5 ： 7$ D、 $5 ： 23$

查看试题解析
6. 已知抛物线 $y^{2} = 4 x$ ，过焦点F的直线与抛物线交于A、B两点，若 $| A B | = \frac{16}{3} ， \vec{A F} = λ \vec{F B} (λ > 1)$ ，则 $λ =$ （）

A、3 B、4 C、5 D、6

查看试题解析
7. 已知函数 $f (x) = A s i n (ω x + φ) ， (A > 0 ， ω > 0 ， | φ | < \frac{π}{2})$ ，两个等式 $f (- x) + f (x - \frac{π}{2}) = 0$ ， $f (x) - f (\frac{π}{2} - x) = 0$ ，对任意实数x均成立， $f (x)$ 在 $(\frac{π}{8} ， \frac{5 π}{28})$ 上单调，则 $ω$ 的最大值为（）

A、17 B、16 C、15 D、13

查看试题解析
8. 对任意正整数对 $(h ， k)$ ，定义函数 $f (h ， k)$ 如下： $f (1 ， j) = 1$ ， $(i + 1) f (i + 1 ， j) = (j - i) f (i ， j) ， i \leq j$ ，则（）

A、 $f (j + 1 ， j) = 1$ B、 $f (i ， j) = 2 C_{j}^{i - 1}$ C、 $\sum_{i = 1}^{j} [j^{2} \cdot f (i ， j)] = j \cdot (2^{j} - 1)$ D、 $\sum_{j = 1}^{n} \sum_{i = 1}^{j} [j \cdot f (i ， j)] = 2^{n} + n - 2$

查看试题解析

二、多选题

9. 下列结论中，正确的有（）

A、数据4，1，6，2，9，5，8的第60百分位数为5 B、若随机变量 $ξ ~ N (1 ， σ^{2}) ， P (ξ \leq - 2) = 0.21$ ，则 $P (ξ \leq 4) = 0.79$ C、已知经验回归方程为 $\hat{y} = \hat{b} x + 1.8$ ，且 $\bar{x} = 2 ， \bar{y} = 20$ ，则 $\hat{b} = 9.1$ D、根据分类变量X与Y的成对样本数据，计算得到 $χ^{2} = 9.632$ ，依据小概率值 $α = 0.001$ 的 $χ^{2}$ 独立性检验 $(x_{0.001} = 10.828)$ ，可判断X与Y有关联，此推断犯错误的概率不大于0.001

查看试题解析
10. 已知函数 $f (x) = x^{3} - 3 x + 1$ ，则（）

A、 $f (x)$ 有两个极值点 B、若方程 $f (x) = a$ 有三个实根，则 $a \leq - 1$ 或 $a \geq 3$ C、点 $(0 ， 1)$ 是曲线 $y = f (x)$ 的对称中心 D、直线 $y = 9 x - 15$ 是曲线 $y = f (x)$ 的切线

查看试题解析
11. 已知正三棱锥 $O - A B C$ 的底面边长为2，表面积为 $\sqrt{3} + \sqrt{7}$ ， A，B，C三点均在以O为球心得球面上， Q为球面上一点，下列结论正确得是（）

A、球O的半径为 $\frac{4}{3}$ B、三棱锥 $O - A B C$ 的内切球半径为 $\frac{\sqrt{21} - 3}{6}$ C、 $\vec{Q A} \cdot \vec{Q B}$ 的取值范围为 $[0 ， \frac{14 + 8 \sqrt{7}}{9}]$ D、若 $Q A ⊥$ 平面ABC，则异面直线AC与QB所成角的余弦值为 $\frac{3 \sqrt{13}}{26}$

查看试题解析
12. 已知F为双曲线 $C ： x^{2} - y^{2} = 1$ 的右焦点，P在双曲线C的右支上，点 $K (\frac{\sqrt{2}}{2} ， 0)$ ．设 $∠ P K F = α$ ， $∠ P F K = β$ ， $∠ K P F = γ$ ，下列判断正确的是（）

A、 $α$ 最大值为 $\frac{π}{3}$ B、 $s i n β \leq \frac{\sqrt{6}}{2} s i n α$ C、 $t a n α = \sqrt{2} s i n β$ D、存在点P满足 $γ = 2 α$

查看试题解析

三、填空题

13. $(3 - \sqrt{x})^{7}$ 展开式中含 $x^{3}$ 项的系数为．

查看试题解析
14. 直线 $3 x + 4 y + c = 0$ 与圆 $x^{2} + y^{2} = 4$ 相交于A，B两点，且 $∠ A O B = 90 °$ （O为坐标原点），则 $c =$ ．

查看试题解析
15. 随着城市经济的发展，早高峰问题越发严重，上班族需要选择合理的出行方式．某公司员工小明上班出行方式由三种，某天早上他选择自驾，坐公交车，骑共享单车的概率分别为 $\frac{1}{3} ， \frac{1}{3} ， \frac{1}{3}$ ，而他自驾，坐公交车，骑共享单车迟到的概率分别为 $\frac{1}{4} ， \frac{1}{5} ， \frac{1}{6}$ ，结果这一天他迟到了，在此条件下，他自驾去上班的概率是．

查看试题解析
16. 已知定义在 $R$ 上可导函数 $f (x)$ ，对于任意的实数x都有 $f (- x) = f (x) - 4 x$ 成立，且当 $x \in (- \infty ， 0)$ 时，都有 $f^{'} (x) < 2 x + 2$ 成立，若 $f (m + 1) \leq f (- m) + 6 m + 3$ ，则实数m的取值范围是．

查看试题解析

四、解答题

17. 在 $△ A B C$ 中，内角A，B，C的对边分别为a，b，c， $\frac{s i n^{2} A}{a} = \frac{c o s A \cdot c o s B + 2 c o s^{2} C}{b}$ ， C为锐角．

(1)、求C；

(2)、若 $a + b = \frac{3 \sqrt{3}}{2} ， c = \sqrt{3}$ ， $△ A B C$ 的面积．

查看试题解析
18. 已知等比数列 ${a_{n}}$ 的前n项和为 $S_{n}$ ，且满足 $\frac{1}{a_{1}} - \frac{1}{a_{2}} = \frac{2}{a_{3}} ， S_{4} = 30$ ，数列 ${b_{n}}$ 满足： $b_{1} = 1$ ， $b_{1} + \frac{1}{2} b_{2} + \frac{1}{3} b_{3} + ⋯ + \frac{1}{n} b_{n} = b_{n + 1} - 1 ， (n \in N^{*})$ ．

(1)、求数列 ${a_{n}}$ ， ${b_{n}}$ 的通项公式；

(2)、设数列 ${c_{n}}$ 的通项 $c_{n} = a_{n} + (- 1)^{n} (3 b_{n} + 1)$ ，求数列 ${c_{n}}$ 的前n项和 $T_{n}$ ．

查看试题解析
19. 第二十二届世界足球赛于2022年11月21日在卡塔尔举行，是历史上首次在中东国家境内举行，也是第二次再亚洲举行的世界杯足球赛，在此火热氛围中，某商场设计了一款足球游戏：场地上共有大、小2个球门，大门和小门依次射门，射进大门后才能进行小门射球，两次均进球后可得到一个世界杯吉祥物“拉伊卜”．已知甲、乙、丙3位顾客射进大门的概率均为 $\frac{3}{4}$ ，射进小门的概率依次为 $\frac{2}{3}$ ， $\frac{1}{3}$ ， $\frac{1}{3}$ ，假设各次进球与否互不影响．

(1)、求这3人中至少有2人射进大门的概率；

(2)、记这3人中得到“拉伊卜”的人数为X，求X的分布列及期望．

查看试题解析
20. 如图，在多面体ABCDE中，面BCDE为平行四边形， $A E = B E = 13$ ， $A B = 8$ ， $B C = 6$ ， $A B ⊥ B C$ ， F为AC中点．

(1)、求证： $A B ⊥ E F$ ；

(2)、二面角 $E - A B - C$ 的正切值为4，求多面体ABCDE的体积．

查看试题解析
21. 已知函数 $f (x) = e^{x} - m l n (m x - m) + m (m > 0)$

(1)、当 $m = 1$ 时，求曲线 $y = f (x)$ 在点 $P (2 ， f (2))$ 处的切线方程；

(2)、若 $f (x) \geq 0$ 恒成立，求实数 $m$ 的取值范围．

查看试题解析
22. 已知椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的离心率为 $\frac{1}{2}$ ，且经过点 $M (- 2 ， 0)$ ， $F_{1} ， F_{2}$ 为椭圆C的左右焦点， $Q (x_{0} ， y_{0})$ 为平面内一个动点，其中 $y_{0} > 0$ ，记直线 $Q F_{1}$ 与椭圆C在x轴上方的交点为 $A (x_{1} ， y_{1})$ ，直线 $Q F_{2}$ 与椭圆C在x轴上方的交点为 $B (x_{2} ， y_{2})$ ．

(1)、求椭圆C的标准方程；

(2)、①若 $A F_{2} ∥ B F_{1}$ ，证明： $\frac{1}{y_{1}} + \frac{1}{y_{2}} = \frac{1}{y_{0}}$ ；
②若 $| Q F_{1} | + | Q F_{2} | = 3$ ，探究 $y_{0} ， y_{1} ， y_{2}$ 之间关系．

查看试题解析