湘豫名校联考2023届高三下学期理数2月入学摸底考试试卷
试卷更新日期:2023-02-24 类型:开学考试
一、单选题
-
1. 已知集合 , ,则( )A、 B、 C、 D、2. 复数的共轭复数是( )A、 B、 C、 D、3. 2022年秋,某京剧演员因疫情原因无法演出,在短视频平台开设自己的账号,不断直播京剧知识.初始直播时已有50名粉丝,经过x天后,粉丝人数满足关系式: , 其中M,k为常数,若开播10天后有200名粉丝,则开播30天后预计该京剧演员在平台上的粉丝数量为( )A、600 B、800 C、3200 D、34004. 函数的图象可能为( )A、
 B、
B、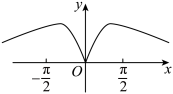 C、
C、 D、
D、 5. 河南一国家级湿地,以其独特的地理环境和良好的生态环境,吸引了全国近三分之一的鸟种在此繁衍生息,成了鸟类自然保护区.天鹅戏水、白鹭觅食,形成了一幅群鸟嬉戏的生态美景.该保护区新建一个椭球形状的观鸟台,椭球的一部分竖直埋于地下,其外观的三视图(单位:米)如下,正视图中椭圆(部分)的长轴长为16米,则该椭球形状观鸟台的最高处到地面的垂直高度为( )
5. 河南一国家级湿地,以其独特的地理环境和良好的生态环境,吸引了全国近三分之一的鸟种在此繁衍生息,成了鸟类自然保护区.天鹅戏水、白鹭觅食,形成了一幅群鸟嬉戏的生态美景.该保护区新建一个椭球形状的观鸟台,椭球的一部分竖直埋于地下,其外观的三视图(单位:米)如下,正视图中椭圆(部分)的长轴长为16米,则该椭球形状观鸟台的最高处到地面的垂直高度为( )
 A、8米 B、10米 C、12米 D、16米6. 执行如图所示的程序框图,若输入k的值为1,则输出n的值为( )
A、8米 B、10米 C、12米 D、16米6. 执行如图所示的程序框图,若输入k的值为1,则输出n的值为( )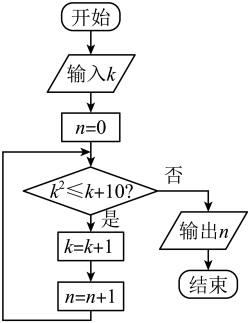 A、2 B、3 C、4 D、57. 若一个数列的后项与其相邻的前项的差值构成的数列为等差数列,则称此数列为二阶等差数列.现有二阶等差数列:2,3,5,8,12,17,23,…,设此数列为 , 若数列满足 , 则数列的前n项和( )A、 B、 C、 D、8. 已知双曲线的左、右焦点分别为 , , 直线与双曲线C交于A,B两点(点A在第二象限),且.则双曲线C的离心率为( )A、 B、 C、 D、9. 某汽车公司最近研发了一款新能源汽车,以单次最大续航里程500公里为标准进行测试,且每辆汽车是否达到标准相互独立,设每辆新能源汽车达到标准的概率为p(),当100辆汽车中恰有80辆达到标准时的概率取最大值时,若预测该款新能源汽车的单次最大续航里程为X,且 , 则预测这款汽车的单次最大续航里程不低于600公里的概率为( )A、0.2 B、0.3 C、0.6 D、0.810. 在中,若内角A,B,C所对的边分别为a,b,c,的平分线交AC于点D,且 , 则周长的最小值为( )A、7 B、 C、 D、411. 某车间生产一种圆台形零件,其下底面的直径为4,上底面的直径为8,已知为上底面的直径,点P是上底面圆周上一点,且 , 是该圆台的一条母线,且 , 则与平面所成的角的正弦值为( )A、 B、 C、 D、12. 设函数的值域为 , 则实数的取值范围是( )A、 B、 C、 D、
A、2 B、3 C、4 D、57. 若一个数列的后项与其相邻的前项的差值构成的数列为等差数列,则称此数列为二阶等差数列.现有二阶等差数列:2,3,5,8,12,17,23,…,设此数列为 , 若数列满足 , 则数列的前n项和( )A、 B、 C、 D、8. 已知双曲线的左、右焦点分别为 , , 直线与双曲线C交于A,B两点(点A在第二象限),且.则双曲线C的离心率为( )A、 B、 C、 D、9. 某汽车公司最近研发了一款新能源汽车,以单次最大续航里程500公里为标准进行测试,且每辆汽车是否达到标准相互独立,设每辆新能源汽车达到标准的概率为p(),当100辆汽车中恰有80辆达到标准时的概率取最大值时,若预测该款新能源汽车的单次最大续航里程为X,且 , 则预测这款汽车的单次最大续航里程不低于600公里的概率为( )A、0.2 B、0.3 C、0.6 D、0.810. 在中,若内角A,B,C所对的边分别为a,b,c,的平分线交AC于点D,且 , 则周长的最小值为( )A、7 B、 C、 D、411. 某车间生产一种圆台形零件,其下底面的直径为4,上底面的直径为8,已知为上底面的直径,点P是上底面圆周上一点,且 , 是该圆台的一条母线,且 , 则与平面所成的角的正弦值为( )A、 B、 C、 D、12. 设函数的值域为 , 则实数的取值范围是( )A、 B、 C、 D、二、填空题
-
13. 已知 , , 且 , 则的最大值是.14. 在的展开式中的系数为 .15. 已知函数 , 若 , , , 则的值为.16. 已知实数 , 函数 , .若方程在上有且仅有4个实数根,则实数的取值范围是.
三、解答题
-
17. 已知数列的前项和为 , 且满足 , , .(1)、证明:数列是等比数列,并求;(2)、设 , 求数列的前项和.18. 抖音(TikTok)是由今日头条推出的一款短视频分享APP,于2016年9月上线,是一个专注于年轻人音乐短视频创作分享的社区平台.抖音的出现是一把双刃剑,可以鼓励人们表达、沟通和记录,让每一个人看见并连接更大的世界,但同时也出现部分网民长时间沉迷刷抖音的现象,长时间刷抖音会影响用眼健康.为了解网民刷抖音的情况,某研究小组从抖音用户中随机抽取100人,对其平均每天刷抖普的时长进行统计,得到统计表如下:
平均每天刷抖音的时长
不大于1小时
大于1小时且小于3小时
不少于3小时
人数(男)
20
25
6
人数(女)
20
15
14
该研究小组按照用户平均每天刷抖音时长将沉迷刷抖音程度分为重度、中度、轻度、若某人平均每天刷抖音的时长不少于3小时则称为“重度沉迷”;平均每天刷抖音的时长大于1小时且小于3小时,叫称为“中度沉迷”;平均每天刷抖音的时长不大于1小时,则称为“轻度沉迷”.
附: , 其中.
0.15
0.10
0.05
0.025
0.010
0.001
2.072
2.706
3.841
5.024
6.635
10.828
(1)、根据调查数据,填写下面列联表,并根据数据判断是否有95%的把握认为性别与是否为“重度沉迷”刷抖音有关系?非“重度沉迷”
“重度沉迷”
合计
人数(男)
人数(女)
合计
(2)、该研究小组为鼓励用户适度刷抖音,从这100名研究对象中按分层抽样的方式随机抽取20位,分别给与“重度沉迷”“中度沉迷”和“轻度沉迷”的抖音用户50元、100元、150元的购书券奖励.现从这20位抖音用户中随机抽取两人,求这两人所获得购书券总和X的分布列和期望.19. 如图,四边形是菱形, , 平面 , , , 设 , 连接 , 交于点 , 连接 , .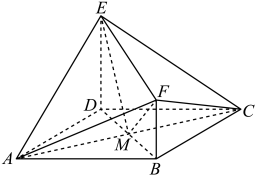 (1)、试问是否存在实数 , 使得平面?若存在,请求出的值,并写出求解过程;若不存在,请说明理由.(2)、当时,求平面与平面所成的锐二面角的余弦值.20. 已知抛物线与椭圆存在相同的焦点,第一象限内曲线上的一点到其焦点的距离为2,直线与相交于两点(不与点重合),直线 , 关于直线对称.(1)、求证:直线的斜率为定值;(2)、若椭圆上存在不同的两点关于直线对称,求原点到直线距离的取值范围.
(1)、试问是否存在实数 , 使得平面?若存在,请求出的值,并写出求解过程;若不存在,请说明理由.(2)、当时,求平面与平面所成的锐二面角的余弦值.20. 已知抛物线与椭圆存在相同的焦点,第一象限内曲线上的一点到其焦点的距离为2,直线与相交于两点(不与点重合),直线 , 关于直线对称.(1)、求证:直线的斜率为定值;(2)、若椭圆上存在不同的两点关于直线对称,求原点到直线距离的取值范围.