山东省济南市2022-2023学年高三下学期数学开学考试试卷
试卷更新日期:2023-02-24 类型:开学考试
一、单选题
-
1. 已知复数 , 其中i是虚数单位,则在复平面内所对应的点在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 已知集合 , , 则( )A、 B、 C、 D、3. 已知向量 , 满足 , , 则向量 , 的夹角为( )A、 B、 C、 D、4. “”的一个充分条件可以是( )A、 B、 C、 D、5. 下图是函数的部分图象,则它的解析式可能是( )
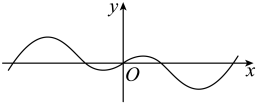 A、 B、 C、 D、6. 已知 , 则( )A、 B、 C、 D、7. 已知等比数列的公比为 , 其前项和为 , 若对任意的恒成立,则的取值范围是( )A、 B、 C、 D、8. 已知 , , , 则( )A、a>b>c B、a>c>b C、b>c>a D、c>b>a
A、 B、 C、 D、6. 已知 , 则( )A、 B、 C、 D、7. 已知等比数列的公比为 , 其前项和为 , 若对任意的恒成立,则的取值范围是( )A、 B、 C、 D、8. 已知 , , , 则( )A、a>b>c B、a>c>b C、b>c>a D、c>b>a二、多选题
-
9. 居家学习期间,某学校发起了“畅读经典,欢度新年”活动,根据统计数据可知,该校共有1200名学生,所有学生每天读书时间均在20分钟到100分钟之间,他们的日阅读时间频率分布直方图如图所示.则下列结论正确的是( )
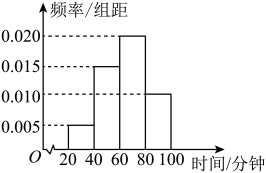 A、该校学生日阅读时间的众数约为70 B、该校学生日阅读时间不低于60分钟的人数约为360 C、该校学生日阅读时间的第50百分位数约为65 D、该校学生日阅读时间的平均数约为6410. 已知函数满足恒成立,且在上单调递增,则下列说法中正确的是( )A、 B、为偶函数 C、若 , 则 D、将图象上所有点的横坐标变为原来的2倍,可以得到的图象11. 如图所示,抛物线E:的焦点为F,过点的直线 , 与E分别相交于 , 和C,D两点,直线AD经过点F,当直线AB垂直于x轴时, . 下列结论正确的是( )
A、该校学生日阅读时间的众数约为70 B、该校学生日阅读时间不低于60分钟的人数约为360 C、该校学生日阅读时间的第50百分位数约为65 D、该校学生日阅读时间的平均数约为6410. 已知函数满足恒成立,且在上单调递增,则下列说法中正确的是( )A、 B、为偶函数 C、若 , 则 D、将图象上所有点的横坐标变为原来的2倍,可以得到的图象11. 如图所示,抛物线E:的焦点为F,过点的直线 , 与E分别相交于 , 和C,D两点,直线AD经过点F,当直线AB垂直于x轴时, . 下列结论正确的是( ) A、E的方程为 B、 C、若AD,BC的斜率分别为 , , 则 D、若AD,BC的倾斜角分别为 , , 则的最大值为12. 在平面四边形ABCD中, , AD=CD=2,AB=1, , 沿AC将折起,使得点B到达点的位置,得到三棱锥 . 则下列说法正确的是( )
A、E的方程为 B、 C、若AD,BC的斜率分别为 , , 则 D、若AD,BC的倾斜角分别为 , , 则的最大值为12. 在平面四边形ABCD中, , AD=CD=2,AB=1, , 沿AC将折起,使得点B到达点的位置,得到三棱锥 . 则下列说法正确的是( ) A、三棱锥体积的最大值为 B、为定值 C、直线AC与所成角的余弦值的取值范围为 D、对任意点 , 线段AD上必存在点N,使得
A、三棱锥体积的最大值为 B、为定值 C、直线AC与所成角的余弦值的取值范围为 D、对任意点 , 线段AD上必存在点N,使得三、填空题
-
13. 为推动黄河流域生态保护和高质量发展,某市环保局派出4个宣传小组,到黄河沿岸5个社区做环保宣讲活动,每个小组至少去1个社区,每个社区只安排1个小组,则不同的安排方法共有种(用数字作答).14. 已知圆锥侧面展开图的周长为 , 面积为 , 则该圆锥的体积为 .15. 已知函数若方程有两个不同的实数根 , 且 , 则实数a的取值范围是 .16. 已知 , 分别为椭圆的左、右焦点,以为圆心且过椭圆左顶点的圆与直线相切.P为椭圆上一点,I为的内心,且 , 则的值为 .
四、解答题
-
17. 甲、乙两人进行抛掷骰子游戏,两人轮流抛掷一枚质地均匀的骰子.规定:先掷出点数6的获胜,游戏结束.(1)、记两人抛掷骰子的总次数为X,若每人最多抛掷两次骰子,求比赛结束时,X的分布列和期望;(2)、已知甲先掷,求甲恰好抛掷n次骰子并获得胜利的概率.18. 已知中,A,B,C所对的边分别为a,b,c,且 .(1)、证明:A=2B;(2)、若a=3,b=2,求的面积.19. 各项均为正数的数列 , 其前n项和记为 , 且满足对 , 都有 .(1)、求数列的通项公式;(2)、设 , 证明: .
