江苏省扬州市2022-2023学年高三下学期数学期初考试试卷

试卷更新日期：2023-02-24 类型：开学考试

进入出卷网下载

一、单选题

1. 若复数z满足 $i (z + i) = 2 + i$ （ $i$ 为虚数单位），则复数z在复平面内所对应的点在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 已知 $a ， b \in R$ ，则“ $a < b$ ”是“ $a < b - 1$ ”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
3. 已知数列 ${a_{n}}$ 满足 $2 a_{n} = a_{n - 1} + a_{n + 1} (n \geq 2) ， a_{3} + a_{4} + a_{5} + a_{6} + a_{7} = 100 ，$ 则其前9项和等于（）

A、150 B、180 C、300 D、360

查看试题解析
4. 平面向量 $\vec{a} ， \vec{b}$ 满足 $\vec{a} + \vec{b} = (3 ， - 2) ， \vec{a} - \vec{b} = (1 ， x)$ ，且 $\vec{a} \cdot \vec{b} = 0$ ，则 $x$ 的值为（）

A、 $\frac{3}{2}$ B、 $\frac{2}{3}$ C、 $\pm 2 \sqrt{3}$ D、 $\pm 2 \sqrt{2}$

查看试题解析
5. 埃及胡夫金字塔是古代世界建筑奇迹之一，其形状可视为一个正四棱锥，已知该金字塔的塔高与底面边长的比满足黄金比例，即比值约为 $\frac{\sqrt{5} - 1}{2}$ ，则它的侧棱与底面所成角的正切直约为（）

A、 $\frac{\sqrt{10} - \sqrt{2}}{2}$ B、 $\frac{\sqrt{5} - 1}{2}$ C、 $\frac{\sqrt{5} + 1}{2}$ D、 $\frac{\sqrt{10} + \sqrt{2}}{2}$

查看试题解析
6. 已知 $α ， β \in (0 ， \frac{π}{2}) ， 2 t a n α = \frac{s i n 2 β}{s i n β + s i n^{2} β}$ ，则 $t a n (2 α + β + \frac{π}{3}) =$ （）

A、 $- \sqrt{3}$ B、 $- \frac{\sqrt{3}}{3}$ C、 $\frac{\sqrt{3}}{3}$ D、 $\sqrt{3}$

查看试题解析
7. 已知一组数据 $x_{1} ， x_{2} ， x_{3} ， x_{4} ， x_{5}$ 的平均数是2，方差是3，则对于以下数据： $2 x_{1} + 1$ ， $2 x_{2} + 1$ ， $2 x_{3} + 1$ ， $2 x_{4} + 1$ ， $2 x_{5} + 1$ ， 1，2，3，4，5下列选项正确的是（）

A、平均数是3，方差是7 B、平均数是4，方差是7 C、平均数是3，方差是8 D、平均数是4，方差是8

查看试题解析
8. 在平面直角坐标系xOy中，x轴正半轴上从左至右四点A､B､C､D横坐标依次为a-c､a､a+c､2a，y轴上点M､N纵坐标分别为m､-2m（m>0），设满足 $| P A | + | P C | = 2 a$ 的动点P的轨迹为曲线E，满 $| Q N | = 2 | Q M |$ 的动点Q的轨迹为曲线F，当动点Q在y轴正半轴上时，DQ交曲线E于点P₀（异于D），且OP₀与BQ交点恰好在曲线F上，则a：c=（）

A、 $\sqrt{2}$ B、 $\sqrt{3}$ C、2 D、3

查看试题解析

二、多选题

9. 下列说法中正确的有（）

A、 $C_{9}^{2} = C_{9}^{7}$ B、 $C_{4}^{2} + C_{4}^{3} = C_{5}^{3}$ C、 $C_{n}^{1} + C_{n}^{2} + C_{n}^{3} + ⋯ + C_{n}^{n} = 2^{n}$ D、 ${(1 + x)}^{4}$ 展开式中二项式系数最大的项为第三项

查看试题解析
10. 已知实数a，b>0，2a+b=4，则下列说法中正确的有（）

A、 $\frac{1}{a} + \frac{1}{b}$ 有最小值 $\frac{3}{2}$ B、a²+b²有最小值 $\frac{16}{5}$ C、4a+2b有最小值8 D、lna+lnb有最小值ln2

查看试题解析
11. 高斯是德国著名数学家，近代数学奠基者之一，享有“数学王子”的称号，用其名字命名的“高斯函数”为：设 $x \in R$ ，用 $[x]$ 表示不超过x的最大整数，则 $y = [x]$ 称为高斯函数.例如 $[- 3.5] = - 4 ， [3.5] = 3 .$ 已知函数 $f (x) = c o s x + | c o s x |$ ，函数 $g (x) = [f (x)] ，$ 则下列说法中正确的有（）

A、函数 $f (x)$ 在区间 $(0 ， π)$ 上单调递增 B、函数 $f (x)$ 图象关于直线 $x = k π (k \in Z)$ 对称 C、函数 $g (x)$ 的值域是 ${0 ， 1 ， 2}$ D、方程 $g (x) = x$ 只有一个实数根

查看试题解析
12. 在四面体 $A B C D$ 的四个面中，有公共棱 $A C$ 的两个面全等， $A D = 1$ ， $C D = \sqrt{2}$ ， $∠ C D A = 90 °$ ，二面角 $B - A C - D$ 大小为 $θ$ ，下列说法中正确的有（）

A、四面体 $A B C D$ 外接球的表面积为 $3 π$ B、四面体 $A B C D$ 体积的最大值为 $\frac{\sqrt{3}}{6}$ C、若 $A D = A B$ ， $A D ⊥ A B$ ，则 $θ = 120 °$ D、若 $A D = B C$ ， $θ = 120 °$ ，则 $B D = \frac{\sqrt{21}}{3}$

查看试题解析

三、填空题

13. 记Sn为等比数列{an}的前n项和.若S₃=4，S₆=12，则S₉=.

查看试题解析
14. 双曲线 $\frac{x^{2}}{4} - \frac{y^{2}}{2} = 1$ 的左､右焦点分别为 $F_{1}$ ， $F_{2}$ ，且右支上有一点 $P (p ， 1)$ ，则 $c o s ∠ F_{1} P F_{2}$ =.

查看试题解析
15. 某个随机数选择器每次从0，1，2，3，4，5，6，7，8，9这10个数字中等可能地选择一个数字，用该随机数选择器连续进行三次选择，选出的数字依次是 $a ， b ， c ，$ 则概率 $P (a < b < c)$ =.

查看试题解析
16. 已知函数 $f (x) = a x^{2} + x$ ，若当 $x \in [0 ， 1]$ 时， $| f (x + 1) | \leq a + 1$ 恒成立，则实数 $a$ 的取值范围是.

查看试题解析

四、解答题

17. 已知数列 ${a_{n}}$ 的前n项和为 $S_{n} ， a_{1} = 2 ， S_{n} = a_{n + 1} - 2 .$

(1)、求数列 ${a_{n}}$ 的通项公式；

(2)、令 $b_{n} = l o g_{2} a_{n} .$ ① $c_{n} = b_{n} \cdot a_{n}$ ；② $c_{n} = \frac{1}{4 b_{n}^{2} - 1}$ ；③ $c_{n} = (- 1)^{n} (b_{n})^{2} ，$ 从上面三个条件中任选一个，求数列 ${c_{n}}$ 的前 $n$ 项和 $T_{n} .$ 注：如果选择多个条件分别解答，按第一个解答计分.

查看试题解析
18. 已知 $△ A B C$ 的内角 $A ， B ， C$ 的对边分别为 $a ， b ， c$ ， $A = \frac{2 π}{3}$ ， $b = 10$ ， $c = 6$ ， $△ A B C$ 的内切圆 $I$ 的面积为 $S$ .

(1)、求 $S$ 的值；

(2)、若点 $D$ 在 $A C$ 上，且 $B ， I ， D$ 三点共线，求 $\vec{B D} \cdot \vec{B C}$ 的值.

查看试题解析
19. 在三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中，侧面 $A C C_{1} A_{1}$ 是菱形， $∠ A_{1} A C = 60 °$ ， $A A_{1} = 2$ ， $A C ⊥ A_{1} B$ .

(1)、求证： $B A = B C$ ；

(2)、已知 $A B = \sqrt{2}$ ， $A_{1} B = 2$ ，求直线 $A_{1} B$ 与平面 $A_{1} B_{1} C$ 所成角的正弦值.

查看试题解析
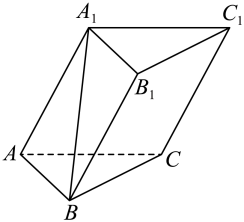20. 云计算是信息技术发展的集中体现，近年来，我国云计算市场规模持续增长.从中国信息通信研究院发布的《云计算白皮书（2022年）》可知，我国2017年至2021年云计算市场规模数据统计表如下：
年份
2017年
2018年
2019年
2020年
2021年
年份代码x
1
2
3
4
5
云计算市场规模y/亿元
692
962
1334
2091
3229
经计算得： $\sum_{i = 1} l n y_{i}$ =36.33， $\sum_{i = 1} (x_{i} l n y_{i})$ =112.85.

(1)、根据以上数据，建立y关于x的回归方程 $\hat{y} = e^{^{\hat{b} x + \hat{a}}}$ （ $e$ 为自然对数的底数）.

(2)、云计算为企业降低生产成本､提升产品质量提供了强大助推力.某企业未引入云计算前，单件产品尺寸与标准品尺寸的误差 $ε ~ N (0 ， \frac{4}{m})$ ，其中m为单件产品的成本（单位：元），且 $P (- 1 < ε < 1)$ =0.6827；引入云计算后，单件产品尺寸与标准品尺寸的误差 $ε ~ N (0 ， \frac{1}{m})$ .若保持单件产品的成本不变，则 $P (- 1 < ε < 1)$ 将会变成多少？若保持产品质量不变（即误差的概率分布不变），则单件产品的成本将会下降多少？
附：对于一组数据 $(x_{1} ， y_{1}) ， (x_{2} ， y_{2}) ， \dots ， (x_{n} ， y_{n}) ，$ 其回归直线 $\hat{y} = \hat{β} x + \hat{α}$ 的斜率和截距的最小二乘估计分别为 $\hat{β}$ = $\frac{\sum_{i = 1}^{n} x_{i} y_{i} - n \bar{x} \bar{y}}{\sum_{i = 1}^{n} {x_{i}}^{2} - n {\bar{x}}^{2}}$ ， $\hat{α} = \bar{y} - \hat{β} \bar{x}$ .
若 $X ~ N (μ ， σ^{2})$ ，则 $P (| X - μ | < σ) = 0.6827$ ， $P (X - μ | < 2 σ) = 0.9545$ ， $P (| X - μ | < 3 σ) = 0.9973 .$

查看试题解析
21. 已知 $A B$ 为抛物线 $G ： y^{2} = 2 p x (p > 0)$ 的弦，点 $C$ 在抛物线的准线 $l$ 上.当 $A B$ 过抛物线焦点 $F$ 且长度为 $8$ 时， $A B$ 中点 $M$ 到 $y$ 轴的距离为 $3$ .

(1)、求抛物线 $G$ 的方程；

(2)、若 $∠ A C B$ 为直角，求证：直线 $A B$ 过定点.

查看试题解析
22. 已知函数 $f (x) = e^{x + 2}$ ， $x \in R ； g (x) = c o s x ，$ $x \in (- \frac{π}{2} ， \frac{π}{2})$ .（ $e$ 为自然对数的底数， $e \approx 2.718$ ）.

(1)、若函数 $h (x) = a f (x) - g (x)$ 在区间 $(- \frac{π}{2} ， \frac{π}{2})$ 上单调递减，求实数a的取值范围；

(2)、是否存在直线l同时与 $y = f (x) ， y = g (x)$ 的图象相切？如果存在，判断l的条数，并证明你的结论；如果不存在，说明理由.

查看试题解析

年份	2017年	2018年	2019年	2020年	2021年
年份代码x	1	2	3	4	5
云计算市场规模y/亿元	692	962	1334	2091	3229