河南省新乡市多校联考2022-2023学年高三下学期理数入学测试试卷

试卷更新日期：2023-02-24 类型：开学考试

进入出卷网下载

一、单选题

1. 已知集合 $A = {4 ， x ， 2 y}$ ， $B = {- 2 ， x^{2} ， 1 - y}$ ，若 $A = B$ ，则实数x的取值集合为（）

A、 ${- 1 ， 0 ， 2}$ B、 ${- 2 ， 2}$ C、 ${- 1 ， 0 ， 2}$ D、 ${- 2 ， 1 ， 2}$

查看试题解析
2. 已知 $z = 1 - 2 i$ ，且 $\frac{a + z}{a \cdot \bar{z}}$ 为实数，则实数 $a =$ （）

A、-2 B、-1 C、1 D、2

查看试题解析
3. 在2022年某地销售的汽车中随机选取1000台，对销售价格与销售数量进行统计，这1000台车辆的销售价格都不小于5万元，小于30万元，将销售价格分为五组： $[5 ， 10) ， [10 ， 15) ， [15 ， 20) ， [20 ， 25) ， [25 ， 30)$ （单位：万元）.统计后制成的频率分布直方图如图所示.在选取的1000台汽车中，销售价格在 $[10 ， 20)$ 内的车辆台数为（）

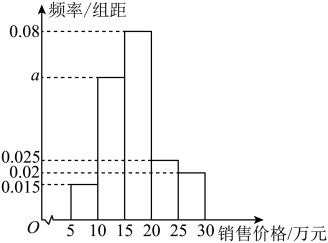A、800 B、600 C、700 D、750

查看试题解析
4. 已知直线l交抛物线 $C ： y^{2} = 18 x$ 于M，N两点，且MN的中点为 $(5 ， 3)$ ，则直线l的斜率为（）

A、 $\frac{9}{5}$ B、 $\frac{3}{2}$ C、3 D、 $\frac{18}{5}$

查看试题解析
5. 已知体积为3的正三棱锥P-ABC，底面边长为 $2 \sqrt{3}$ ，其内切球为球O，若在此三棱锥中再放入球 $O^{'}$ ，使其与三个侧面及内切球O均相切，则球 $O^{'}$ 的半径为（）

A、 $\frac{\sqrt{3}}{3}$ B、 $\frac{1}{9}$ C、 $\frac{\sqrt{2}}{3}$ D、 $\frac{\sqrt{3}}{9}$

查看试题解析
6. 古希腊毕达哥拉斯学派的数学家研究过各种多边形数.如三角形数1，3，6，10，第n个三角形数为 $\frac{n (n + 1)}{2} = \frac{1}{2} n^{2} + \frac{1}{2} n$ .记第n个k边形数为 $N (n ， k) (k \geq 3)$ ，以下列出了部分k边形数中第n个数的表达式：
三角形数： $N (n ， 3) = \frac{1}{2} n^{2} + \frac{1}{2} n$
正方形数： $N (n ， 4) = n^{2}$
五边形数： $N (n ， 5) = \frac{3}{2} n^{2} - \frac{1}{2} n$
六边形数： $N (n ， 6) = 2 n^{2} - n$
可以推测 $N (n ， k)$ 的表达式，由此计算 $N (20 ， 23) =$ （）

A、4020 B、4010 C、4210 D、4120

查看试题解析
7. 如图，程序框图的算法思路源于欧几里得在公元前300年左右提出的“辗转相除法”执行该程序框图，若输入 $m = 2022$ ， $n = 1314$ ，则输出m的值为（）

A、6 B、12 C、18 D、24

查看试题解析
8. 若二项式 ${(2 x - \frac{1}{\sqrt{x}})}^{n} (n \in N^{*})$ 的展开式中只有第5项的二项式系数最大，则展开式中 $x^{2}$ 项的系数为（）

A、 $- 1120$ B、 $- 1792$ C、1792 D、1120

查看试题解析
9. 已知函数 $f (x) = A s i n (ω x + φ) (A > 0 ， ω > 0 ， | φ | < \frac{π}{2})$ 的图象向右平移 $\frac{π}{6}$ 个单位长度后得到函数 $g (x)$ 的图象，若 $g (x)$ 图象相邻对称轴间的距离为 $\frac{π}{2}$ ，对任意x，都有 $g (- x) + g (x) = 0$ ，且 $f (0) = \sqrt{3}$ ，则（）

A、 $f (x)$ 的最大值为 $\sqrt{3}$ B、 $f (x)$ 的图象关于点 $(\frac{2 π}{3} ， 0)$ 中心对称 C、 $f (x)$ 的图象关于直线 $x = \frac{π}{6}$ 对称 D、 $f (x)$ 在 $[- \frac{5 π}{12} ， \frac{π}{12}]$ 上单调递增

查看试题解析
10. 已知函数 $f (x) = {\begin{array}{l} x^{2} - 2 a x + 9 ， x \leq 1 ， \\ 2 x + \frac{2}{x - 1} ， x > 1 ， \end{array}$ 若 $f (x)$ 的最小值为6，则实数a的取值范围是（）

A、 $[1 ， 2]$ B、 $[- \sqrt{3} ， 3]$ C、 $[- \sqrt{3} ， 2]$ D、 $[- 2 ， 2]$

查看试题解析
11. 设函数 $f (x)$ 在 $R$ 上的导函数为 $f^{^{'}} (x)$ ， $f (x) + f (- x) = 0$ ，对任意 $x \in (0 ， + \infty)$ ，都有 $f (x) f^{'} (x) > x$ ，且 $f (1) = 2$ ，则不等式 $[f (x - 1)]^{2} < x^{2} - 2 x + 4$ 的解集为（）

A、 $(- \infty ， 0) ∪ (2 ， + \infty)$ B、 $(0 ， 2)$ C、 $(1 ， 3)$ D、 $(- \infty ， 1) ∪ (3 ， + \infty)$

查看试题解析
12. 已知 $S_{n}$ 是数列 ${a_{n}}$ 的前n项和， $a_{1} = 1$ ， $S_{n} + S_{n + 1} = n (n + 2)$ ，则 $\frac{S_{2024}}{S_{2023}} =$ （）

A、 $\frac{1013}{1012}$ B、 $\frac{2023}{2024}$ C、 $\frac{2025}{2023}$ D、 $\frac{1013}{1011}$

查看试题解析

二、填空题

13. 已知向量 $\vec{a} = (4 ， - 2)$ ， $\vec{b} = (2 ， λ)$ ，若 $\vec{a} ⊥ (\vec{a} - \vec{b})$ ，则 $λ =$ .

查看试题解析
14. 方程 $\frac{50}{1 0^{x} + 1} - 5 = 1 0^{x + 1}$ 的实数解为.

查看试题解析
15. 在长方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $A D = 1$ ， $A A_{1} = 2$ ， $A B = 3$ ， M是棱 $C_{1} D_{1}$ 上一点，且 $D_{1} M = 1$ ，则异面直线CD与BM所成角的余弦值为.

查看试题解析
16. 已知双曲线 $x^{2} - \frac{y^{2}}{3} = 1$ 的左右焦点为 $F_{1}$ 、 $F_{2}$ ，过 $F_{2}$ 的直线与双曲线右支交于A、B两点，则 $△ A F_{1} F_{2}$ 、 $△ B F_{1} F_{2}$ 的内切圆面积之和的取值范围是．

查看试题解析

三、解答题

17. 在 $△ A B C$ 中，设角A，B，C所对的边分别为a，b，c， $b = \sqrt{3}$ ，且 $b = 2 a s i n (C + \frac{π}{6})$ .

(1)、求角A；

(2)、若D为AB的中点，且 $C D = 1$ ，求 $△ A B C$ 的面积.

查看试题解析
18. 在数字化时代，电子书阅读给人们的阅读方式､认知模式与思维习惯带来了改变，电子书阅读的快速增长也再次引发人们对相关问题的思考.某地对本地群众（中老年人与年轻人）的年龄与阅读习惯（经常电子阅读与经常纸质阅读）进行了调查统计，得到如下列联表：

年轻人
中老年人
合计
经常电子阅读
50
35
85
经常纸质阅读
x
y
115
合计
M
N
200
设从经常电子阅读的人中任取1人，记抽取到的中老年人数为 $ξ$ ；从经常纸质阅读的人中任取1人，记抽取到的中老年人数为 $η$ ，已知 $P (ξ = 0) = \frac{23}{17} P (η = 0)$ .
参考公式及数据：
$K^{2} = \frac{n (a d - b c)^{2}}{(a + b) (c + d) (a + c) (b + d)}$ ，其中 $n = a + b + c + d$ .
$P (K^{2} \geq k_{0})$
0.10
0.05
0.010
0.005
$k_{0}$
2.706
3.841
6.635
7.879

(1)、求列联表中x，y，M，N的值，并判断是否有95%的把握认为阅读习惯与年龄有关；

(2)、从年轻人中按阅读习惯用分层抽样的方法抽出10人，再从抽出的10人中用简单随机抽样的方法抽取3人，若其中经常电子阅读的人数为X，求X的分布列及数学期望.

查看试题解析
19. 在四棱锥P-ABCD中，底面ABCD是矩形， $P A ⊥$ 平面ABCD， $P A = A D = 8$ .以AC的中点O为球心，AC为直径的球面交PD于点M.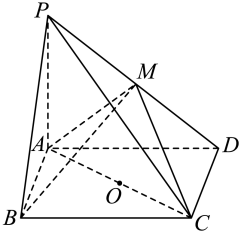

(1)、证明：M为PD的中点.

(2)、若二面角B-AM-C的余弦值为 $\frac{\sqrt{3}}{3}$ ，求AB.

查看试题解析
20. 已知椭圆 $C ： \frac{x^{2}}{4} + y^{2} = 1$ ， $△ P A B$ 的三个顶点都在椭圆C上，且P为椭圆C的左顶点，直线AB经过点 $(- 1 ， 0)$ .

(1)、求 $△ P A B$ 面积的最大值.

(2)、若 $△ P A B$ 三边所在的直线斜率都存在，且分别记为 $k_{P A} ， k_{P B} ， k_{A B}$ ，试判断 $k_{A B} (k_{P A} + k_{P B})$ 是否为定值.若是，求出该定值；若不是，请说明理由.

查看试题解析
21. 已知函数 $f (x) = \frac{e^{x}}{x^{2}} - a x + 2 a l n x$ .

(1)、判断 $f (x)$ 极值点的个数；

(2)、当 $a ≤ e$ 时，证明： $f (x) \geq 0$ .

查看试题解析
22. 在直角坐标系xOy中，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线 $C_{1}$ 的极坐标方程为 $ρ c o s (θ + \frac{π}{4}) = \sqrt{2}$ ，曲线 $C_{2}$ 的极坐标方程为 $ρ^{2} - 2 ρ c o s θ - 3 = 0$ .

(1)、求曲线 $C_{1}$ 和曲线 $C_{2}$ 的直角坐标方程；

(2)、设 $P (3 ， 1)$ ，曲线 $C_{1}$ 与曲线 $C_{2}$ 的交点为A，B，求 $\frac{| P A | + | P B |}{| A B |}$ 的值.

查看试题解析
23. 已知函数 $f (x) = | x + a | + | x - 2 a |$ .

(1)、当 $a = 1$ 时，求不等式 $f (x) \leq 5$ .

(2)、若对任意 $x \in R$ ， $f (x) \geq 2 a^{2}$ 成立，求a的取值范围.

查看试题解析

	年轻人	中老年人	合计
经常电子阅读	50	35	85
经常纸质阅读	x	y	115
合计	M	N	200

$P (K^{2} \geq k_{0})$	0.10	0.05	0.010	0.005
$k_{0}$	2.706	3.841	6.635	7.879