广东省汕头市潮南区2023届高三下学期数学期初摸底试卷

试卷更新日期：2023-02-24 类型：开学考试

进入出卷网下载

一、单选题

1. 已知集合 $M$ ， $N$ ，若 $M = {- 1 ， 1}$ ， $M ∪ N = {- 1 ， 0 ， 1}$ ，则（）

A、 $M \subseteq N$ B、 $N \subseteq M$ C、 $M \cap N = \emptyset$ D、 $0 \in N$

查看试题解析
2. 已知复数 $z_{1} = 4 - 7 i ， z_{2} = m + 2 i (m \in R)$ ， $\frac{z_{2}}{z_{1}}$ 在复平面内，复数所对应的点位于第三象限的一个充分不必要条件是（）

A、 $m < - 2$ B、 $m < - \frac{8}{7}$ C、 $- \frac{8}{7} < m < \frac{7}{2}$ D、 $m < \frac{7}{2}$

查看试题解析
3. 中国空间站的主体结构包括天和核心舱、问天实验舱和梦天实验舱．假设中国空间站要安排甲，乙，丙，丁，戊5名航天员开展实验，其中天和核心舱安排3人，问天实验舱与梦天实验舱各安排1人．若甲、乙两人不能同时在一个舱内做实验，则不同的安排方案共有（）

A、8种 B、14种 C、20种 D、116种

查看试题解析
4. 如图，将一个球放入一个倒立的圆锥形容器中，圆锥的高为3，底面半径为4，且圆锥的底面恰好经过球心，则该球的表面积为（）

A、 $16 π$ B、 $\frac{476}{25} π$ C、 $\frac{576}{25} π$ D、 $64 π$

查看试题解析
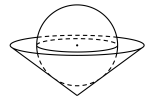5. 核酸检测分析是用荧光定量 $P C R$ 法，通过化学物质的荧光信号，对在 $P C R$ 扩增进程中成指数级增加的靶标 $D N A$ 实时监测，在 $P C R$ 扩增的指数时期，荧光信号强度达到阈值时， $D N A$ 的数量 $X_{n}$ 与扩增次数 $n$ 满足 $\lg X_{n} = n \lg (1 + p) + \lg X_{0}$ ，其中 $p$ 为扩增效率， $X_{0}$ 为 $D N A$ 的初始数量.已知某被测标本 $D N A$ 扩增 $10$ 次后，数量变为原来的 $100$ 倍，那么该样本的扩增效率 $p$ 约为（）
(参考数据： $10^{0.2} \approx 1.585$ ， $10^{- 0.2} \approx 0.631$ )

A、0.369 B、0.415 C、0.585 D、0.631

查看试题解析
6. 已知A，F分别是双曲线 $C ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的右顶点和左焦点，O是坐标原点.点P在第一象限且在C的渐近线上，满足PA⊥AF.若OP平分∠APF，则双曲线C的离心率为（）

A、2 B、 $\sqrt{3}$ C、3 D、 $\frac{3}{2}$

查看试题解析
7. 某干燥塔的底面是半径为1的圆面 $O$ ，圆面有一个内接正方形 $A B C D$ 框架，在圆 $O$ 的劣弧 $B C$ 上有一点 $P$ ，现在从点 $P$ 出发，安装 $P A ， P B ， P C$ 三根热管，则三根热管的长度和的最大值为（）

A、4 B、 $2 \sqrt{3}$ C、 $3 \sqrt{3}$ D、 $2 \sqrt{6}$

查看试题解析
8. 已知角A为△ABC中一个内角，如果适当排列sinA，cosA，tanA的顺序，可使它们成为一个等比数列，那么角A的大小属于区间（）

A、 $(0 ， \frac{π}{4})$ B、 $(\frac{π}{4} ， \frac{π}{2})$ C、 $(\frac{π}{2} ， \frac{3 π}{4})$ D、 $(\frac{3 π}{4} ， π)$

查看试题解析

二、多选题

9. 有一组样本数据 $x_{1} ， x_{2} ， ⋯ ， x_{n}$ ，其样本平均数为 $\bar{x}$ .现加入一个新数据 $x_{n + 1}$ ，且 $x_{n + 1} <$ $\bar{x}$ ，组成新的样本数据 $x_{1} ， x_{2} ， ⋯ ， x_{n} ， x_{n + 1}$ ，与原样本数据相比，新的样本数据可能（）

A、平均数不变 B、众数不变 C、极差变小 D、第20百分位数变大

查看试题解析
10. 函数 $f (x) = 2 s i n (ω x + φ) (0 < ω < 3 ， 0 < φ < \frac{π}{2})$ 的最小正周期为 $T$ ，若 $f (T) = \sqrt{3} ， x = \frac{π}{3}$ 为 $f (x)$ 的零点，则（）

A、 $T = 2 π$ B、函数 $f (x)$ 的图象可由函数 $y = 2 c o s ω x$ 的图象向右平移 $\frac{π}{12}$ 个单位得到 C、 $f (x)$ 在 $[0 ， 2 π]$ 内有4个极值点 D、函数 $y = f (x) - 1$ 在 $[- \frac{π}{4} ， \frac{π}{4}]$ 仅有1个零点

查看试题解析
11. 函数 $f (x) = \frac{b}{| x | - a} (a > 0 ， b > 0)$ 的图象类似于汉字“囧”字，被称为“囧函数”，并把其与y轴的交点关于原点的对称点称为“囧点”，以“囧点”为圆心，凡是与“囧函数”有公共点的圆，皆称之为“囧圆”，则当 $a = 1$ ， $b = 1$ 时，下列结论正确的是（）

A、函数 $f (x)$ 的图象关于直线 $x = 1$ 对称 B、当 $x \in (- 1 ， 1)$ 时， $f (x)$ 的最大值为－1 C、函数 $f (x)$ 的“囧点”与函数 $y = l n x$ 图象上的点的最短距离为 $\sqrt{2}$ D、函数 $f (x)$ 的所有“囧圆”中，面积的最小值为3π

查看试题解析
12. 已知正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的棱长均为 $2 ， E$ 为线段 $A A_{1}$ 的中点， $\vec{A P} = λ \vec{A B} + μ \vec{A D}$ ，其中 $λ ， μ \in [0 ， 1]$ ，则下列选项正确的是（）

A、当 $μ = \frac{1}{2}$ 时， $A_{1} P ⊥ E D_{1}$ B、当 $λ = μ$ 时， $A_{1} P + P D$ 的最小值为 $\sqrt{2} + \sqrt{5}$ C、若直线 $B_{1} P$ 与平面 $A B C D$ 所成角为 $\frac{π}{4}$ ，则点 $P$ 的轨迹长度为 $\frac{π}{2}$ D、当 $λ + μ = 1$ 时，正方体被平面 $P A D_{1}$ 截的图形最大面积为 $4 \sqrt{2}$

查看试题解析

三、填空题

13. 在 $(2 x + y + 1)^{5}$ 的展开式中， $x^{3} y^{2}$ 的系数为.

查看试题解析
14. 已知向量 $\vec{a} = (2 ， 1) ， \vec{b} = (x ， 3)$ ，若 $\vec{b}$ 在 $\vec{a}$ 方向上的投影向量为 $\vec{a}$ ，则 $x$ 的值为.

查看试题解析
15. 已知等差数列 ${a_{n}}$ 的公差为 $d$ ，随机变量 $X$ 满足 $P (X = i) = a_{i} (0 < a_{i} < 1) ， i = 1 ， 2 ， 3 ， 4$ ，则 $d$ 的取值范围为.

查看试题解析
16. 已知函数 $f (x) = e^{x} - e^{2 - x}$ ，所有满足 $f (a) + f (b) = 0$ 的点 $(a ， b)$ 中，有且只有一个在圆 $C$ 上，则圆 $C$ 的方程可以是.（写出一个满足条件的圆的方程即可）

查看试题解析

四、解答题

17. 已知正项数列 ${a_{n}}$ 的前n项和为 $S_{n}$ ，且满足 $a_{n}^{2} = 2 a_{n} S_{n} - 1$ .

(1)、证明：数列 ${S_{n}^{2}}$ 是等差数列；

(2)、设数列 ${\frac{1}{S_{n}}}$ 的前n项和为 $T_{n}$ ，证明： $T_{100} > 18$

查看试题解析
18. 记 $△ A B C$ 的内角 $A ， B ， C$ 的对边分别为 $a ， b ， c$ ，满足 $2 b c o s C = 2 a + c$ ， $D$ 是边 $A C$ 上的点，且 $B D = 2 ， ∠ D B C = \frac{π}{6}$ .

(1)、求 $∠ A B C$ ；

(2)、求 $S_{△ A B C}$ 的最小值.

查看试题解析
19. 2022年卡塔尔世界杯将11月20日开赛，某国家队为考察甲、乙两名球员对球队的贡献，现作如下数据统计：

球队胜
球队负
总计
甲参加
30
$b$
60
甲未参加
$c$
10
$f$
总计
60
$e$
n
乙球员能够胜任前锋､中场､后卫三个位置，且出场率分别为：0.1，0.5，0.4；在乙出任前锋、中场、后卫的条件下，球队输球的概率依次为：0.2，0.2，0.7
附表：
$α$
0.15
0.10
0.05
0.025
0.010
0.005
0.001
$x_{α}$
2.072
2.706
3.841
5.024
6.635
7.879
10.828

(1)、根据小概率值 $α$ =0.025的独立性检验，能否认为该球队胜利与甲球员参赛有关联？

(2)、根据数据统计，问：
①当乙参加比赛时，求该球队某场比赛输球的概率；
②当乙参加比赛时，在球队输了某场比赛的条件下，求乙球员担当中场的概率；
③如果你是教练员，应用概率统计有关知识，该如何使用乙球员？

查看试题解析
20. 如图，在以P，A，B，C，D为顶点的五面体中，平面ABCD为等腰梯形， $A B / / C D ， A D = C D = \frac{1}{2} A B$ ，平面PAD⊥平面PAB， $P A ⊥ P B$ .

(1)、求证：△PAD为直角三角形；

(2)、若 $A D = P B$ ，求直线PD与平面PBC所成角的正弦值.

查看试题解析
21. 设椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的左､右顶点分别为 $A ， B$ ，上顶点为 $D$ ，点 $P$ 是椭圆上异于顶点的动点，已知椭圆的右焦点为 $F (\sqrt{3} ， 0)$ ，且经过点 $(\sqrt{3} ， \frac{1}{2})$ .

(1)、求椭圆 $C$ 的方程；

(2)、若直线 $A D$ 与直线 $B P$ 交于点 $M$ ，直线 $D P$ 与 $x$ 轴交于点 $N$ ，求证：直线 $M N$ 恒过某定点，并求出该定点.

查看试题解析
22. 已知函数 $f (x) = l n x - \frac{a + 1}{x}$ ， $g (x) = a (x - 2) e^{1 - x} - 1$ ，其中 $a \in$ R.

(1)、讨论 $f (x)$ 的单调性；

(2)、当 $0 < a < \frac{5}{3}$ 时，是否存在 $x_{1} ， x_{2}$ ，且 $x_{1} \neq x_{2}$ ，使得 $f (x_{i}) = g (x_{i}) (i = 1 ， 2)$ ？证明你的结论.

查看试题解析

	球队胜	球队负	总计
甲参加	30	$b$	60
甲未参加	$c$	10	$f$
总计	60	$e$	n

$α$	0.15	0.10	0.05	0.025	0.010	0.005	0.001
$x_{α}$	2.072	2.706	3.841	5.024	6.635	7.879	10.828