广东省揭阳市普宁国贤学校2023届高三下学期数学开学考试试卷

试卷更新日期：2023-02-24 类型：开学考试

进入出卷网下载

一、单选题

1. 若集合 $M = {x | 2^{x} > - 1}$ ， $N = {x | - 1 < x < 2}$ ，则 $M \cap N =$ （）

A、 ${x | x > - 1}$ B、 ${x | x < 2}$ C、 ${x | - 1 < x < 2}$ D、 ${x | 0 < x < 2}$

查看试题解析
2. 已知 $a ， b \in R$ ， $i$ 是虚数单位，若 $a + 2 i$ 与 $1 + b i$ 互为共轭复数，则 ${(a + b i)}^{2} =$ （）

A、 $5 - 4 i$ B、 $5 + 4 i$ C、 $- 3 - 4 i$ D、 $- 3 + 4 i$

查看试题解析
3. “ $m = - 1$ ”是“直线 $x + m y - 2 = 0$ 与直线 $x - y + n = 0$ 平行”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
4. 小明和李华在玩游戏，他们分别从1~9这9个正整数中选出一个数告诉老师，老师经过计算后得知他们选择的两个数不相同，且两数之差为偶数，那么小明选择的数是偶数的概率是（）

A、 $\frac{3}{8}$ B、 $\frac{4}{9}$ C、 $\frac{9}{16}$ D、 $\frac{1}{2}$

查看试题解析
5. 若函数 $f (x) = {\begin{array}{l} a^{x} ， 2 < x ⩽ a \\ l o g_{a} (x - 2) ， x > a \end{array}$ (其中 $a > 0 ， a \neq 1$ )存在零点，则实数 $a$ 的取值范围是（）

A、 $(\frac{1}{2} ， 1) \cup (1 ， 3)$ B、(1，3] C、(2，3) D、(2，3]

查看试题解析
6. 已知 $f (x)$ 为奇函数，当 $x \geq 0$ 时， $f (x) = x^{2} - 4^{x} + m$ ，则当 $x < 0$ 时， $f (x) =$ （）

A、 $x^{2} - 4^{- x} + 1$ B、 $- x^{2} - 4^{- x} - 1$ C、 $- x^{2} + 4^{- x} - 1$ D、 $- x^{2} + 4^{- x} + 1$

查看试题解析
7. 现有下列五个结论：
①若 $a ， b \in R$ ，则有 $| a b | = | a | | b |$ ；
②对任意向量 $\vec{a}$ 、 $\vec{b}$ ，有 $| \vec{a} \cdot \vec{b} | = | \vec{a} | | \vec{b} |$ ；
③对任意向量 $\vec{a}$ 、 $\vec{b}$ ，有 ${\vec{a}}^{2} = | \vec{a} |^{2}$ ；
④对任意复数 $z$ ，有 $z^{2} = | z |^{2}$ ；
⑤对任意复数 $z$ ，有 $| z^{2} | = | z |^{2}$ ．
以上结论中，正确的个数为（）

A、0 B、1 C、2 D、3

查看试题解析
8. 如图，已知正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的棱长为 $1 ， M ， N$ 分别是棱 $A A_{1} ， B C$ 上的动点，若 $M N = \sqrt{2}$ ，则线段 $M N$ 的中点 $P$ 的轨迹是（）

A、一条线段 B、一段圆弧 C、一部分球面 D、两条平行线段

查看试题解析

二、多选题

9. 有一组样本数据 $x_{1} ， x_{2} ， ⋯ ， x_{n}$ ，其样本平均数为 $\bar{x}$ .现加入一个新数据 $x_{n + 1}$ ，且 $x_{n + 1} <$ $\bar{x}$ ，组成新的样本数据 $x_{1} ， x_{2} ， ⋯ ， x_{n} ， x_{n + 1}$ ，与原样本数据相比，新的样本数据可能（）

A、平均数不变 B、众数不变 C、极差变小 D、第20百分位数变大

查看试题解析
10. 已知O为坐标原点，点 $A (c o s θ ， s i n θ)$ ， $B (c o s (θ + \frac{2 π}{3}) ， s i n (θ + \frac{2 π}{3}))$ ， $C (c o s (θ + \frac{4 π}{3}) ， s i n (θ + \frac{4 π}{3}))$ ，则（）

A、 $| A B | = | B C |$ B、 $\vec{O A} + \vec{O B} = \vec{C O}$ C、 $\vec{O A} \cdot \vec{O B} < 0$ D、 $\vec{O A} \cdot (\vec{O B} + \vec{O C}) > 0$

查看试题解析
11. 双曲线具有如下光学性质：如图 $F_{1}$ ， $F_{2}$ 是双曲线的左、右焦点，从右焦点 $F_{2}$ 发出的光线m交双曲线右支于点P，经双曲线反射后，反射光线n的反向延长线过左焦点 $F_{1}$ ．若双曲线C的方程为 $\frac{x^{2}}{9} - \frac{y^{2}}{16} = 1$ ，下列结论正确的是（）

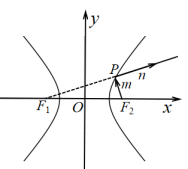A、若 $m ⊥ n$ ，则 $| P F_{1} | \cdot | P F_{2} | = 16$ B、当n过 $Q (7 ， 5)$ 时，光由 $F_{2} \to P \to Q$ 所经过的路程为13 C、射线n所在直线的斜率为k，则 $| k | \in [0 ， \frac{4}{3})$ D、若 $T (1 ， 0)$ ，直线PT与C相切，则 $| P F_{2} | = 12$

查看试题解析
12. 在数列 ${a_{n}}$ 中，对于任意的 $n \in N^{*}$ 都有 $a_{n} > 0$ ，且 $a_{n + 1}^{2} - a_{n + 1} = a_{n}$ ，则下列结论正确的是（）

A、对于任意的 $n \geq 2$ ，都有 $a_{n} > 1$ B、对于任意的 $a_{1} > 0$ ，数列 ${a_{n}}$ 不可能为常数列 C、若 $0 < a_{1} < 2$ ，则数列 ${a_{n}}$ 为递增数列 D、若 $a_{1} > 2$ ，则当 $n \geq 2$ 时， $2 < a_{n} < a_{1}$

查看试题解析

三、填空题

13. ${(x^{2} + y + 3)}^{6}$ 中 $x^{4} y$ 的系数为（用数字作答）.

查看试题解析
14. 已知 $s i n (2 x - \frac{π}{6}) + \frac{1}{3} = \sqrt{3} s i n (x + \frac{π}{6})$ ，则 $s i n (x + \frac{π}{6}) =$ .

查看试题解析
15. 已知 $f (x) = \frac{s i n x}{2^{x} - a \cdot 2^{- x}}$ 为奇函数，则 $a =$ ．

查看试题解析
16. 球体在工业领域有广泛的应用，某零件由两个球体构成，球 $O_{1}$ 的半径为 $10 ， P ， Q$ 为球 $O_{1}$ 表面上两动点， $P Q = 16 ， M$ 为线段 $P Q$ 的中点.半径为2的球 $O_{2}$ 在球 $O_{1}$ 的内壁滚动，点 $A ， B ， C$ 在球 $O_{2}$ 表面上，点 $O_{2}$ 在截面 $A B C$ 上的投影 $H$ 恰为 $A C$ 的中点，若 $O_{2} H = 1$ ，则三棱锥 $M - A B C$ 体积的最大值是.

查看试题解析

四、解答题

17. 已知数列 ${a_{n}}$ 满足 $S_{n} = \frac{n (a_{1} + a_{n})}{2}$ ，其中 $S_{n}$ 是 ${a_{n}}$ 的前 $n$ 项和.

(1)、求证： ${a_{n}}$ 是等差数列；

(2)、若 $a_{1} = 1 ， a_{2} = 2$ ，求 $b_{n} = \frac{2^{n} (1 - a_{n})}{a_{n} a_{n + 1}}$ 的前 $n$ 项和 $T_{n}$ .

查看试题解析
18. 如图，在四棱锥 $P - A B C D$ 中，底面 $A B C D$ 为矩形，平面 $P A B ⊥$ 平面 $A B C D ， O$ 为 $A B$ 中点， $A C$ 与 $O D$ 交于点 $E ， △ P A B$ 的重心为 $G$ .

(1)、求证： $E G$ $/ /$ 平面 $P C D$

(2)、若 $P A = P B = 5 ， A B = 8 ， B C = 4$ ，求二面角 $C - G E - D$ 的正弦值.

查看试题解析
19. 如图，已知 $\vec{O M} = \vec{a} ， \vec{O N} = \vec{b}$ ，平面内任意点 $A$ 关于点 $M$ 的对称点为 $B$ ，点 $B$ 关于点 $N$ 的对称点为 $C$ .设 $\vec{a} - \vec{b} = \vec{e}$ （ $\vec{e}$ 为单位向量）.

(1)、求 $A C$ 的长；

(2)、在 $△ A B C$ 中，若 $A B s i n 2 B = A C s i n C$ ，试求 $A B + B C$ 的取值范围.

查看试题解析
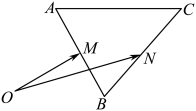20. 某工厂生产一批零件，其直径X满足正态分布 $X \sim N (10 ， 0.25)$ （单位： $m m$ ）.

(1)、现随机抽取15个零件进行检测，认为直径在 $(8.5 ， 11.5)$ 之内的产品为合格品，若样品中有次品则可以认定生产过程中存在问题.求上述事件发生的概率，并说明这一标准的合理性.（已知： $P (μ - 3 σ < X < μ + 3 σ) = 0.9973 ， 0.997 3^{15} \approx 0.9603$ ）

(2)、若在上述检测中发现了问题，另抽取100个零件进一步检测，则这100个零件中的次品数最可能是多少？

查看试题解析
21. 已知抛物线C： $y^{2} = 2 p x (p > 0)$ 与直线 $y = x + 2$ 相切．

(1)、求C的方程；

(2)、过C的焦点F的直线l与C交于A，B两点，AB的中垂线与C的准线交于点P，若 $| P A | = \frac{\sqrt{3}}{2} | A B |$ ，求l的方程．

查看试题解析
22. 已知函数 $f (x) = e^{x} + x s i n x + c o s x - a x - 2 (a \in R)$ .

(1)、若 $a = 2$ ，求曲线 $y = f (x)$ 在点 $(0 ， f (0))$ 处的切线方程；

(2)、若 $f (x) \geq 0$ 对任意的 $x \in [0 ， + \infty)$ 恒成立，求 $a$ 的取值范围.

查看试题解析