安徽省皖江名校联盟2023届高三下学期数学第五次联考（开学摸底）试卷

试卷更新日期：2023-02-24 类型：开学考试

进入出卷网下载

一、单选题

1. 已知集合 $M = {x | l o g_{2} x < 1}$ |，集合 $N = {x | - 1 < x < 1}$ ，则 $M \cup N =$ （）

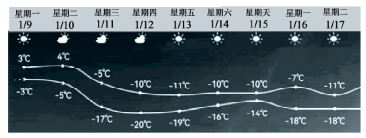
A、 $(0 ， 1)$ B、 $(- 1 ， 2)$ C、 $(0 ， 2)$ D、 $(- \infty ， 2)$

查看试题解析
2. 2022年三九天从农历腊月十八开始计算，也就是2023年1月9日至17日，是我国北方地区一年中最冷的时间．下图是北方某市三九天气预报气温图，则下列对这9天判断错误的是（）

A、昼夜温差最大为12℃ B、昼夜温差最小为4℃ C、有3天昼夜温差大于10℃ D、有3天昼夜温差小于7℃

查看试题解析
3. 已知 $s i n θ + 2 c o s^{2} \frac{θ}{2} = \frac{5}{4}$ ，则 $s i n 2 θ =$ （）

A、 $- \frac{15}{16}$ B、 $\frac{15}{16}$ C、 $- \frac{3}{4}$ D、 $\frac{3}{4}$

查看试题解析
4. 在 $△ A B C$ 中， $B C = 2$ ， $\vec{A B} \cdot \vec{A C} = 8$ ，若D是BC的中点，则 $A D =$ （）

A、1 B、3 C、4 D、5

查看试题解析
5. 已知函数 $f (x) = s i n (ω x + φ) (ω > 0 ， | φ | < \frac{π}{2})$ 图象上相邻两条对称轴之间的距离为 $\frac{π}{2}$ ，将函数 $y = f (x)$ 的图象向左平移 $\frac{π}{3}$ 个单位后，得到的图象关于y轴对称，则函数 $f (x)$ 的一个零点是（）

A、 $\frac{π}{6}$ B、 $\frac{π}{12}$ C、 $\frac{π}{3}$ D、 $\frac{5 π}{12}$

查看试题解析
6. 已知 $⊙ O$ ， $x^{2} + y^{2} = 4$ ， $⊙ C$ 与一条坐标轴相切，圆心在直线 $x - y + 7 = 0$ 上．若 $⊙ C$ 与 $⊙ O$ 相切，则满足条件的 $⊙ C$ 有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 已知圆锥DO的轴截面为等边三角形， $△ A B C$ 是底面 $⊙ O$ 的内接正三角形，点P在DO上，且 $P O = λ D O$ ．若 $P A ⊥$ 平面PBC，则实数 $λ =$ （）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{6}}{3}$ C、 $\frac{\sqrt{6}}{4}$ D、 $\frac{\sqrt{6}}{6}$

查看试题解析
8. 已知动圆过定点 $M (0 ， 4)$ ，且在x轴上截得的弦AB的长为8．过此动圆圆心轨迹C上一个定点 $P (m ， 2)$ 引它的两条弦PS，PT，若直线PS，PT的倾斜角互为补角，记直线ST的斜率为k，则 $m k =$ （）

A、4 B、2 C、 $- 4$ D、 $- 2$

查看试题解析

二、多选题

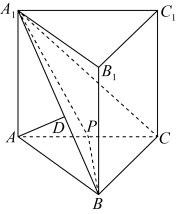
9. 数列 ${a_{n}}$ 满足： $a_{1} = 1$ ， $a_{1} + a_{2} + a_{3} + \cdot \cdot \cdot + a_{n - 1} = 4 a_{n} (n \geq 2)$ ，则下列结论中正确的是（）

A、 $a_{2} = \frac{1}{4}$ B、 $a_{n + 1} = \frac{5}{4} a_{n}$ ， $n \geq 2$ C、 ${a_{n}}$ 是等比数列 D、 $a_{1} + a_{2} + a_{3} + \cdot \cdot \cdot + a_{n} = {(\frac{5}{4})}^{n - 1}$ ， $n \in N^{*}$

查看试题解析
10. 已知e是自然对数的底数，则下列不等关系中正确的是（）

A、 $e^{π} > 3^{e}$ B、 $π^{e} < e^{π}$ C、 $2^{e} < e^{2}$ D、 $e^{3} < 3^{e}$

查看试题解析
11. 已知 $f (x) (x \in R)$ 为偶函数，且 $f (x - \frac{3}{2}) = f (x + \frac{1}{2})$ 恒成立．当 $x \in [2 ， 3]$ 时 $f (x) = x$ ．则下列四个命题中，正确的是（）

A、 $f (x)$ 的周期是 $2 k (k \neq 0 ， k \in Z)$ B、 $f (x)$ 的图象关于点 $(1 ， 0)$ 对称 C、当 $x \in [- 3 ， - 2]$ 时， $f (x) = - x$ D、当 $x \in [- 2 ， 0]$ 时， $f (x) = 3 - | x + 1 |$

查看试题解析
12. 已知正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的棱长为1，E，F分别是棱 $A_{1} D_{1}$ 和棱 $C_{1} D_{1}$ 的中点，G为棱BC上的动点（不含端点）．下列说法中正确的是（）

A、当G为棱BC的中点时， $△ E F G$ 是锐角三角形 B、三棱锥 $D_{1} - E F G$ 的体积为定值 C、 $△ E F G$ 面积的取值范围是 $(\frac{3}{8} ， \frac{\sqrt{17}}{8})$ D、若异面直线AB与EG所成的角为 $α$ ，则 $s i n α \in [\frac{\sqrt{2}}{2} ， \frac{\sqrt{5}}{3})$

查看试题解析

三、填空题

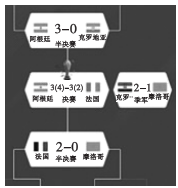
13. 若复数 $z = \frac{i}{2 - i}$ （i是虚数单位）的共轭复数是 $\bar{z}$ ，则 $z - \bar{z}$ 的虚部是．

查看试题解析
14. 2022年12月18日在卡塔尔世界杯决赛中，阿根廷队以总分7比5战胜法国队，历时28天的2022卡塔尔世界杯也缓缓落下了帷幕．随后某电视台轮流播放半决赛及以后的这4场足球赛（如图），某人随机选3场进行观看，其中恰好总决赛、季军赛被选上的概率为．

查看试题解析
15. 过点 $A (0 ， 1)$ 作斜率为k的直线l交双曲线 $x^{2} - \frac{y^{2}}{2} = 1$ 于 $P_{1}$ ， $P_{2}$ 两点，线段 $P_{1} P_{2}$ 的中点在直线 $x = \frac{1}{2}$ 上，则实数k的值为．

查看试题解析
16. 已知直线l与曲线 $y = e^{x}$ 、 $y = 2 + l n x$ 都相切，则直线l的方程为．

查看试题解析

四、解答题

17. 在锐角 $△ A B C$ 中，BC在AB上的投影长等于 $△ A B C$ 的外接圆半径R．

(1)、求 $s i n A c o s B$ 的值；

(2)、若 $4 c o s A s i n B = 1$ ，且 $A B = 3$ ，求R．

查看试题解析
18. 2022年北京冬奥会圆满落幕，随后多所学校掀起了“雪上运动”的热潮．为了解学生对“雪上运动”的喜爱程度，某学校从全校学生中随机抽取200名学生进行问卷调查，得到以下数据：

喜欢雪上运动
不喜欢雪上运动
合计
男生
80
40
女生
30
50
合计

(1)、完成 $2 \times 2$ 列联表，依据小概率值 $α = 0.01$ 的 $χ^{2}$ 独立性检验，能否认为是否喜欢雪上运动与性别有关联？

(2)、①从随机抽取的这200名学生中采用分层抽样的方法抽取20人，再从这20人中随机抽取3人．记事件 $A =$ “至少有2名是男生”，事件 $B =$ “至少有2名喜欢雪上运动的男生”，事件 $C =$ “至多有1名喜欢雪上运动的女生”．试计算 $P (A) \cdot P (B | A) \cdot P (C | A B)$ 和 $P (A B C)$ 的值，并比较它们的大小．
②①中 $P (A B C)$ 与 $P (A) \cdot P (B | A) \cdot P (C | A B)$ 的大小关系能否推广到更一般的情形？请写出结论，并说明理由．
参考公式及数据 $χ^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$ ， $n = a + b + c + d$ ．
$α$
0.10
0.05
0.010
0.001
$x_{α}$
2.706
3.841
6.635
10.828

查看试题解析
19. 已知数列 ${a_{n}}$ 的各项均为正数，其前n项和为 $S_{n}$ ，且 $a_{n}^{2} - 2 S_{n} \cdot a_{n} + 1 = 0$ ．

(1)、求 $a_{n}$ 和 $S_{n}$ ；

(2)、若 $n \geq 3$ ，证明： $\frac{1}{S_{1}^{2}} + \frac{1}{S_{2}^{2}} + \cdot \cdot \cdot + \frac{1}{S_{n}^{2}} > 2 (1 - \frac{1}{2^{n}})$ ．

查看试题解析
20. 如图，在直三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中， $A D ⊥$ 平面 $A_{1} B C$ ，其垂足 $D$ 落在直线 $A_{1} B$ 上．

(1)、求证： $B C ⊥ A_{1} B$

(2)、若 $A D = \sqrt{3} ， A B = B C = 2 ， P$ 为 $A C$ 的中点，求二面角 $P - A_{1} B - A$ 的平面角的余弦值

查看试题解析
21. 已知 $F_{1}$ ， $F_{2}$ 为椭圆C： $\frac{x^{2}}{2} + y^{2} = 1$ 的左右焦点，P为椭圆C上一点．若 $△ P F_{1} F_{2}$ 为直角三角形，且 $| P F_{1} | \geq | P F_{2} |$ ．

(1)、求 $\frac{| P F_{1} |}{| P F_{2} |}$ 的值；

(2)、若直线l： $y = k x + m (k \neq 0)$ 与椭圆C交于A，B两点，线段AB的垂直平分线经过点 $N (0 ， - \frac{1}{2})$ ，求实数m的取值范围．

查看试题解析
22. 已知函数 $f (x) = e^{x} + a c o s x$ ，其中 $x > 0$ ， $a \in R$ ．

(1)、当 $a = - 1$ 时，讨论 $f (x)$ 的单调性；

(2)、若函数 $f (x)$ 的导函数 $f^{'} (x)$ 在 $(0 ， π)$ 内有且仅有一个极值点，求a的取值范围．

查看试题解析

	喜欢雪上运动	不喜欢雪上运动	合计
男生	80	40
女生	30	50
合计

$α$	0.10	0.05	0.010	0.001
$x_{α}$	2.706	3.841	6.635	10.828