初中数学同步训练必刷题（北师大版七年级下册3.2 用关系式表示的变量间关系）

试卷更新日期：2023-02-23 类型：同步测试

进入 出卷网 下载

一、单选题

  • 1. 在某次实验中，测得两个变量m和v之间的4组对应数据如下表：

    m

    1

    2

    3

    4

    v

    2.01

    4.9

    10.03

    17.1

    则m与v之间的关系最接近于下列各关系式中的（  ）

    A、v=2m B、v=m2+1 C、v=3m-1 D、v=m+1

    查看试题解析

  • 2. 瓶子或者罐头盒等圆柱形的物体常常如图所示那样堆放着，随着层数的增加，物体总数也会发生变化，数据如表，则下列说法错误的是（   ）

    层数n/层

    1

    2

    3

    4

    5

    ……

    物体总数y/个

    1

    3

    6

    10

    15

    ……

    A、在这个变化过程中层数是自变量，物体总数是因变量 B、当堆放层数为7层时，物体总数为28个 C、物体的总数随着层数的增加而均匀增加 D、物体的总数y与层数n之间的关系式为 y = n ( n + 1 ) 2

    查看试题解析

  • 3. 如图，李大爷用24米长的篱笆靠墙围成一个矩形 (ABCD) 菜园，若菜园靠墙的一边 (AD) 长为 x （米），那么菜园的面积 y （平方米）与 x 的关系式为（   ） 

     

    A、y=x(12−x)2 B、y=x(12−x) C、y=x(24−x)2 D、y=x(24−x)

    查看试题解析

  • 4. 如果一盒圆珠笔有16支，售价24元，用y（元）表示圆珠笔的售价，x表示圆珠笔的支数，那么y与x间的关系式为（   ）. 
    A、y=12x B、y=18x C、y=23x D、y=32x

    查看试题解析

  • 5. 在烧开水时，水温达到  1 0 0 ° C  水就会沸腾，下表是小红同学做“观察水的沸腾”实验时所记录的变量时间  t ( m i n )  和温度  T ( ° C )  的数据：          
     

      t ( m i n )  

    		  

     0 

    		  

     2 

    		  

     4 

    		  

     6 

    		  

     8 

    		  

     10 

    		  

     12 

    		  

     14 

    		  

     … 
     

      T ( ° C )  

    		  

     30 

    		  

     44 

    		  

     58 

    		  

     72 

    		  

     86 

    		  

     100 

    		  

     100 

    		  

     100 

    		  

     … 

     在水烧开之前（即  t < 1 0  ），温度  T  与时间  t  的关系式及因变量分别为（   ） 

    A、 T = 7 t + 3 0  ，  T B、 T = 1 4 t + 3 0  ，  t C、 T = 1 4 t − 1 6  ，  t D、 T = 3 0 t − 1 4  ，  T

    查看试题解析

  • 6. 长方形的周长为12cm ， 其中一边的长为x(0<x<6)cm ， 面积为ycm2 ， 则该长方形中y与x的关系式是（  ）
    A、y=(12−x)2 B、y=(6−x)2 C、y=x(12−x) D、y=x(6−x)

    查看试题解析

  • 7. 长方形的周长为24cm，其中一边为  x ( x > 0 )  ，面积为  y c m 2  ，则y与x的关系可以表示为（   ）. 
    A、 y = x 2 B、 y = ( 1 2 − x ) 2 C、 y = 1 2 x − x 2 D、 y = 2 4 − 2 x

    查看试题解析

  • 8. 如果每盒水笔有10支，售价16元，用y（元）表示水笔的售价，x表示水笔的支数，那么y与x之间的关系应该是（  ）
    A、y=10x B、y=16x C、y=58x D、y=85x

    查看试题解析

  • 9. 一个长方形的周长为30，则长方形的面积y与长方形一边长x的关系式为（ ）
    A、y=x(15-x) B、y=x(30-x) C、y=x(30-2x) D、y=x(15+x)

    查看试题解析

  • 10. 已知圆柱的高为3 cm，当圆柱的底面半径r(cm)由小变大时，圆柱的体积V(cm3)随之变化，则V与r的关系式是 （ ）
    A、V=πr2 B、V=9πr2 C、V= 13 πr2 D、V=3πr2

    查看试题解析

二、填空题

  • 11. 随着各行各业有序复工复产，企业提倡员工实行“两点一线”上下班模式，减少不必要的聚集.小华爸爸早上开车以 60km/h 的平均速度行驶 20min 到达单位，下班按原路返回，若返回时平均速度为 v ，则路上所用时间 t （单位： h ）与速度v（单位： km/h ）之间的关系可表示为. 

    查看试题解析

  • 12. 小颖准备乘出租车到距家超过3km的科技馆参观，出租车的收费标准如下：             
     

    里程数/km

         		 

     收费/元 

     
     

    3km以内(含3km)

         		 

     8.00 

     
     

    3km以外每增加1km

         		 

     1.80 

     

    则小颖应付车费y(元)与行驶里程数x(km)之间的关系式为.

    查看试题解析

  • 13. 已知变量y与x的部分对应值如表格所示，则y与x的关系式是.          
     

     x 

         		 

     … 

         		 

     1 

         		 

     2 

         		 

     3 

         		 

     4 

         		 

     … 

     
     

     y 

         		 

     … 

         		 

     12 

         		 

     14 

         		 

     16 

         		 

     18 

         		 

     … 

     

    查看试题解析

  • 14. 如图，某计算装置有一数据输入口A和一运算结果的输出口B，如表是小明输入的一些数据和这些数据经该装置计算后输出的相应结果按照这个计算装置的计算规律，若输入的数是n，则输出的数是. 

     

     

    A 1 2 3 4 5
    B 2 5 10 17 26

    查看试题解析

  • 15. 某梯形上底长、下底长分别是x，y，高是6，面积是24，则y与x之间的关系式是. 

    查看试题解析

  • 16. 如图，是汽车加油站在加油过程中加油器仪表某一瞬间的显示，（其中数量用x升表示，金额用y元表示，单价用a元/升表示），结合图片信息，请用适当的方式表示加油过程中变量之间的关系为：. 

     

    查看试题解析

  • 17. 一个弹簧，不挂物体时长为10厘米，挂上物体后弹簧会变长，每挂上1千克物体，弹簧就会伸长1.5cm.如果挂上的物体的总质量为x千克时，弹簧的长度为为ycm，那么y与x的关系可表示为y＝. 

    查看试题解析

  • 18. 如图，三角形ABC的高AD=4，BC=6，点E在BC上运动，若设BE的长为x ， 三角形ACE的面积为有y，则y与x的关系式为.

    查看试题解析

三、解答题

  • 19.
    按如图方式摆放餐桌和椅子．用x来表示餐桌的张数，用y来表示可坐人数． 

     ①题中有几个变量？ 

     ②你能写出两个变量之间的关系吗？ 

     

    查看试题解析

  • 20. “五一”小长假期间，小天和父母一起开车到距家220千米的景点旅游，出发前，汽车油箱内储油45升，当行驶了180千米时，发现油箱余油量为27升（假设行驶过程中汽车的耗油量是均匀的）．
    (1)、求该车平均每千米的耗油量；
    (2)、写出油箱余油量Q（升）与行驶路程x（千米）的关系式；
    (3)、当油箱中剩余油量低于3升时，汽车将自动报警，如果往返途中不加油，他们能否在汽车报警前沿原路返回到家？请说明理由．

    查看试题解析

  • 21. 如图，把一些相同规格的碗整齐地叠放在水平桌面上，这摞碗的高度随着碗的数量变化而变化的情况如表格所示：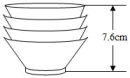

    数量/只

    1

    2

    3

    4

    5

    …

    高度/cm

    4

    5.2

    6.4

    7.6

    8.8

    …

    (1)、上述两个变量之间的关系中，哪个是自变量？哪个是因变量？
    (2)、用h（cm）表示这摞碗的高度，用x（只）表示这摞碗的数量，请用含有x的代数式表示h；
    (3)、若这摞碗的高度为 11.2cm，求这摞碗的数量.

    查看试题解析

  • 22. 为了解某种品牌小汽车的耗油量，我们对这种车在高速公路上做了耗油试验，并把试验的数据记录下来，制成下表：

    汽车行驶时间t（h）

    0

    1

    2

    3

    …

    油箱剩余油量Q（L）

    100

    94

    88

    82

    …

    ①根据上表的数据，请你写出Q与t的关系式；
    ②汽车行驶5h后，油箱中的剩余油量是多少；
    ③该品牌汽车的油箱加满50L，若以100km/h的速度匀速行驶，该车最多能行驶多远．

    查看试题解析

  • 23. 科学家研究发现声音在空气中传播的速度y（米/秒）与气温x（℃）有关：当气温是0℃时，音速是330米/秒；当气温是5℃时，音速是333米秒；当气温是10℃时，音速是336米/秒；当气温是15℃时，音速是339米/秒；当气温是20℃时，音速是342米/秒；当气温是25℃时，音速是345米/秒；当气温是30℃时，音速是348米/秒.
    (1)、请用表格表示气温与音速之间的关系；
    (2)、表格反映了哪两个变量之间的关系？哪个是自变量？哪个是因变量？
    (3)、当气温是35℃时，估计音速y可能是多少？
    (4)、用一个式子来表示两个变量之间的关系.

    查看试题解析

  • 24. 父亲告诉张云：“距离地面越高，温度越低”，并给张云出示了下面的表格：

    距离地面高度（千米） 

    0 

    1 

    2 

    3 

    4 

    5 

    温度（℃） 

    20 

    14 

    8 

    2 

    -4 

    -10 

    根据上表，父亲还给张云出了下面几个问题，请你和张云一起回答．

    (1)、上表反映了哪两个变量之间的关系？哪个是自变量？哪个是因变量？
    (2)、如果用h表示距离地面的高度，用t表示温度，那么随着h的变化，t是怎么变化的？
    (3)、你能猜出距离地面6千米的高空温度是多少吗？

    查看试题解析